• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ХАРАКТЕРИСТИКИ ЛАНОК ДРУГОГО ПОРЯДКУ

ПЕРЕДАТНI ФУНКЦІЇ, ЧАСТОТНI ТА ЧАСОВI

В загальному випадку ланка другого порядку має операторну передатну функцiю

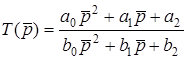. (12.1)

В окремих випадках деякi коефiцiєнти можуть дорiвнювати нулю.

Розглянемо три основнi випадки.

1. .

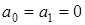, (12.2)

де 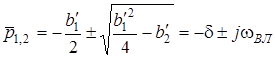- полюси функцiї 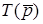(або коренi знаменника); 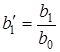; 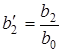- нормованi коефiцiєнти.

Коренi будуть комплексно-спряженими, якщо виконується умова

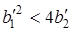або або .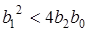

Визначимо частотнi характеристики. Згiдно з (12.2) комплексний коефiцiєнт передачi має вигляд:

,

де 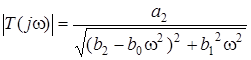- АЧХ; 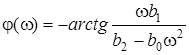- ФЧХ.

Проаналiзуємо вигляд АЧХ: значення на нульовiй частотi становить 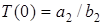; максимальне значення АЧХ матиме, коли знаменник буде мiнiмальним, тобто коли 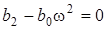. При цьому ;

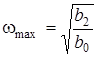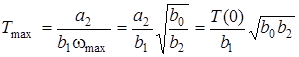. (12.3)

Фазо-частотна характеристика на частотi 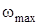дорiвнюватиме

.

Аналiз ФЧХ показує, що ; .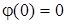

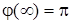Якщо коренi кратнi, то 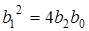; . Тодi

.

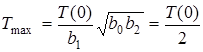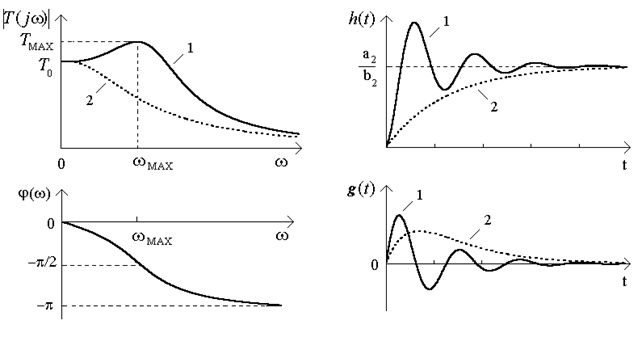
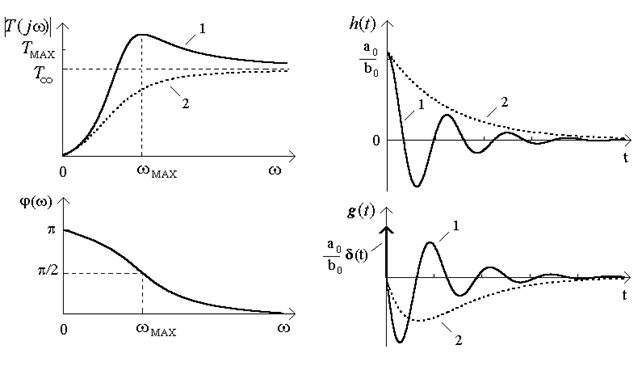
Графiки АЧХ i ФЧХ для ланки другого порядку типу (12.2) для випадку комплексно-спряжених (крива 1) та кратних (крива 2) коренiв зображено на рис.12.1а. Аналізуючи графiк АЧХ, робимо висновок, що передатна функцiя (12.2) вiдповiдає схемi фiльтра нижнiх частот (ФНЧ).

а) б)

Рисунок 12.1

Розглянемо часовi характеристики ланки (12.2). Для цього скористаємось спiввiдношенням (11.1)

. (12.4)

Для визначення перехiдної характеристики подамо 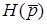у виглядi суми простих дробiв

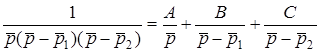. (12.5)

Приведемо до загального знаменника i прирiвняємо коефiцiєнти при однакових степенях чисельника

;

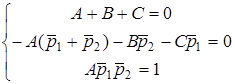; (12.6)

З третього рiвняння системи (12.6) отримуємо 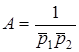; з першого рівняння: 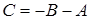; 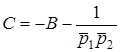. Пiдставимо значення коефiцiєнтiв A i C до другого рiвняння системи (12.6):

; .

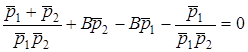У пiдсумку матимемо такi значення коефiцiєнтiв:

; ;

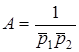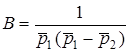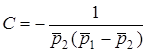
Це виведення справедливе для дiйсних та комплексно-спряжених коренiв (окрiм кратних). Для дiйсних коренiв коефіцієнти A,B,C - дiйснi числа; для комплексно-спряжених коренiв A - дiйсне число, 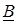i 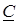- комплекснi числа, причому

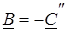. (12.7)

Отже, на основi (12.5) матимемо

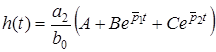. (12.8)

Перевiримо виконання граничних спiввiдношень (11.15). Для цього розрахуємо коефiцiєнт A:

.

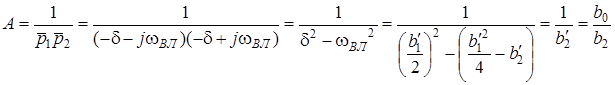Тодi .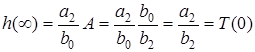

З (12.6) виходить, що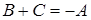, тодi .

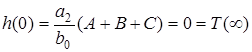Отже, граничнi спiввiдношення виконуються.

Вираз (12.8) є слушним для простих коренiв. Спираючись на нього, можна показати, що з урахуванням (12.7) для комплексно-спряжених коренiв формула (12.8) набуває вигляду

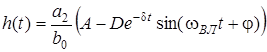, (12.9)

де коефiцiєнти D та j - деякi дiйснi числа:

; ; .

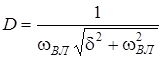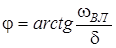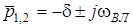Графiки функцiї згiдно з (12.8) i (12.9) зображено на рис.12.1б (комплекснi коренi - крива 1, дiйснi - крива 2).

Встановимо зв'язок мiж часовими та частотними характеристиками. Вiдомо, що для кола другого порядку сталу часу можна визначити, якщо порiвняти 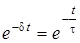. Тодi .

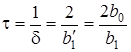Згiдно з (12.3)

.

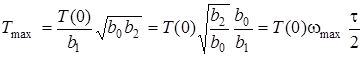Тодi

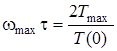. (12.10)

Якщо 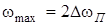; a 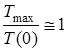, то (12.10) пiдтверджує висновок, що добуток смуги пропускання i сталої часу є величина постiйна i для кола другого порядку дорiвнює двом.

Використовуючи зв'язок мiж перехiдною та iмпульсною характеристикою, знайдемо вираз для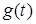

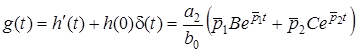. (12.11)

Можна показати, що вираз (12.11) для комплексно-спряжених коренiв перетворюється у такий вигляд

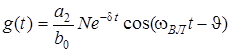, (12.12)

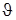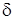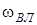де коефiцiєнти N, є дiйсними числами, i можуть бути вираженi через значення коефiцiєнтiв i . Оскiльки

,

то з (12.12) виходить, що .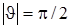

Графiк функцiї 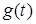зображено на рис.12.1б.

2. .

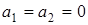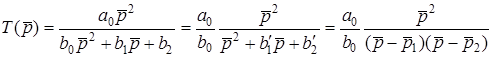. (12.13)

Функцiя (12.13) має нуль подвiйної кратностi i два полюси 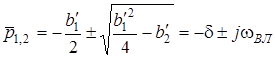. Так саме, як для ФНЧ, коренi T(p) будуть комплексно-спряженими, якщо .

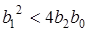Знайдемо частотнi характеристики. Згiдно з (12.13) комплексний коефiцiєнт передачi має вигляд

,

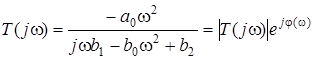де 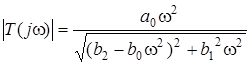- А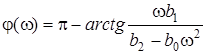ЧХ; - ФЧХ

Проаналiзуємо вигляд АЧХ: значення на нульовiй частотi 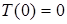; якщо частота прямує до нескiнченностi, ; максимальне значення АЧХ матиме, коли знаменник прийме мiнiмальне значення, тобто коли 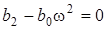. При цьому ;

.

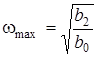Фазо-частотна характеристика на частотi 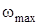дорiвнюватиме

.

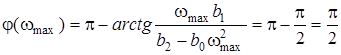Аналiз ФЧХ показує, що 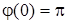. Якщо , тодi 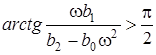(оскiльки реальна частина знаменника 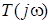менша за нуль). В такому разi .

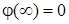Графiки АЧХ i ФЧХ для ланки другого порядку типу (12.13) для випадку комплексно-спряжених (крива 1) і кратних коренiв (крива 2) зображено на рис.12.2а. Розглядаючи графiк АЧХ, робимо висновок, що передатна функцiя (12.13) вiдповiдає схемi фiльтра верхнiх частот (ФВЧ).

а) б)

Рисунок 12.2

Розглянемо часовi характеристики ланки (12.13). Для цього скористаємось спiввiдношенням (11.1)

. (12.14)

Для визначення перехiдної характеристики подамо 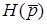у виглядi суми простих дробiв

.

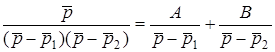Зведемо до загального знаменника i прирiвняємо коефiцiєнти при однакових степенях чисельника: .

; .

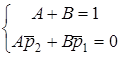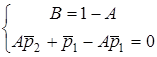Розв'язавши цю систему вiдносно коефiцiєнтiв A i B, матимемо

; .

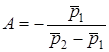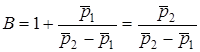Тодi

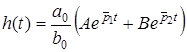. (12.15)

Перевiримо виконання граничних спiввiдношень

; .

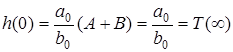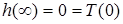Знайдемо вираз для перехiдної характеристики за умови, що коренi є комплексно-спряженими числами. Покажемо, що тодi виконується спiввiдношення .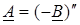

,

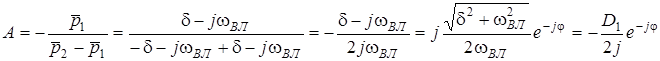
де ; .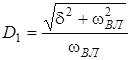

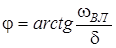Пiдставимо значення коефiцiєнтiв A і B до (12.15)

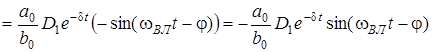. (12.16)

В останньому виразi враховано вiдому формулу 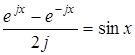. Графiки функцiї згiдно з (12.15) i (12.16) зображено на рис. 12.2б.

Встановимо зв'язок мiж часовими та частотними характеристиками. Так саме, як для ланки ФНЧ, стала часу дорiвнює

,

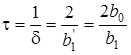а максимальне значення 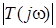становить

.

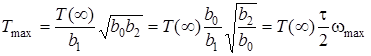Тодi

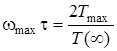. (12.17)

Цей вираз є аналогiчним виразу (12.10).

Iмпульсну характеристику ланки (12.13) знайдемо операторним методом:

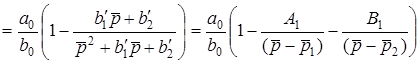. (12.18)

Переходячи вiд зображення (12.18) до оригiналу, матимемо:

, (12.19)

де 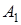, 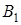- деякi коефiцiєнти, якi визначаються при розкладаннi на простi дроби, аналогiчно (12.5). Приблизний вигляд графiка 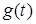для комплексно-спряжених коренiв зображено на рис.12.2б.

3. .

Операторна передатна функцiя

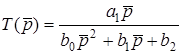. (12.20)

Комплексна передатна функцiя

,

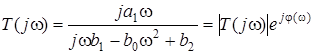де 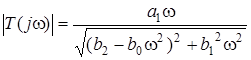- АЧХ; 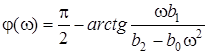- ФЧХ.

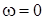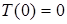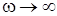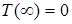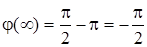Проаналiзуємо характернi точки частотних характеристик: 1) , , ; 2) , , ; 3) , , ;.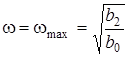

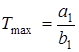Приблизнi графiки частотних характеристик ланки (12.20) зображено на рис.12.3а. Аналiзуючи графiки, робимо висновок, що 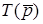даного типу вiдповiдає смугопропускному фiльтру (СФ).

Часовi характеристики ланки (12.20) можна отримати операторним способом аналогiчно виведенню, яке зроблене в пунктах 1,2. Так, перехiдна характеристика визначатиметься виразом:

.

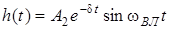Приблизний вигляд графiкiв часових характеристик для комплексно-спряжених коренiв зображено на рис.12.3б.

Можна показати також, що для ланки СФ стала часу дорiвнює 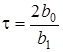, а смуга пропускання приблизно дорiвнює значенню 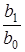, тобто виконується спiввiдношення .

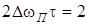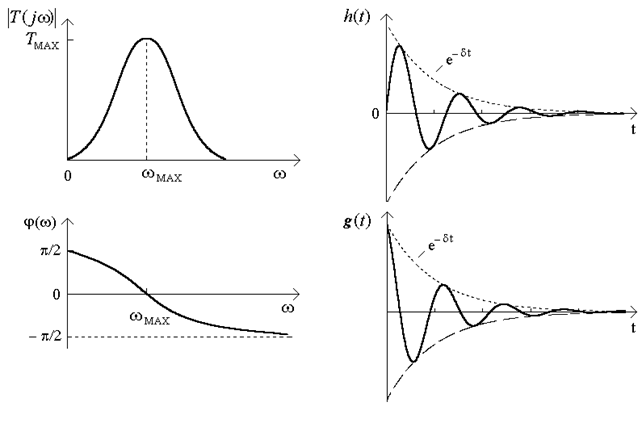
а) б)

Рисунок 12.3

Читайте також:

1. RLC-фільтр четвертого порядку
2. V. Поняття та ознаки (характеристики) злочинності
3. Акустичні характеристики порід
4. Аспекти організаційного порядку
5. Афінний шифр k-ro порядку.
6. Бінарне відношення порядку.
7. Будова, принцип роботи та характеристики МДН – транзисторів
8. Будова, принцип роботи та характеристики тиристорів
9. Будова, характеристики і параметри біполярного транзистора
10. Варіаційні ряди та їх характеристики
11. Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
12. Вестфальский мир як основа європейського правопорядку 1648-1815 рр.

Переглядів: 1469