
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТА ЧАСОВИМИ ХАРАКТЕРИСТИКАМИ
ЗВ'ЯЗОК МIЖ ОПЕРАТОРНИМИ, ЧАСТОТНИМИ
11.1 Зв'язок мiж операторною характеристикою кола
i зображеннями часових характеристик
Нехай на входi ЛЕК дiє коливання 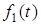 , яке викликає вiдповiдну реакцiю на виходi
, яке викликає вiдповiдну реакцiю на виходi  .
.
1. Якщо 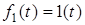 , то за визначенням перехiдної характеристики
, то за визначенням перехiдної характеристики 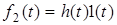 . Якщо перейти до зображень, то
. Якщо перейти до зображень, то 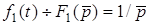 ;
; 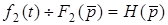 . Згiдно з визначенням операторної характеристики
. Згiдно з визначенням операторної характеристики 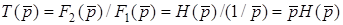 .Тодi
.Тодi
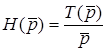 . (11.1)
. (11.1)
Вираз (11.1) визначає операторний спосiб знаходження перехiдної характеристики.
2. Якщо 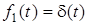 , то за визначенням iмпульсної характеристики
, то за визначенням iмпульсної характеристики 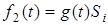 . Знайдемо зображення функцiї
. Знайдемо зображення функцiї 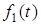 за допомогою прямого перетворення Лапласа
за допомогою прямого перетворення Лапласа
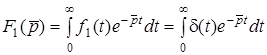 . (11.2)
. (11.2)
У формулi (11.2) пiдiнтегральна функцiя вiдмiнна вiд нуля тiльки там, де не дорiвнює нулю дельта-функцiя 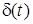 , тобто при
, тобто при 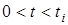 ,
, 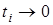 (фiльтрувальна властивiсть). Але при нескiнченно малiй тривалостi iмпульсу
(фiльтрувальна властивiсть). Але при нескiнченно малiй тривалостi iмпульсу
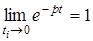 , тому
, тому 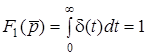 .
.
Отже  ,
, 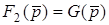 . Тодi
. Тодi
 . (11.3)
. (11.3)
Приклад. Для кола (рис.10.1а) розглянемо переходи вiд 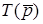 до
до 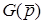 i вiд
i вiд 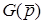 до
до 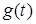 . Вище для цього кола було отримано вираз (10.1) для операторної характеристики
. Вище для цього кола було отримано вираз (10.1) для операторної характеристики 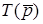 . Згiдно з (11.3) зображення iмпульсної характеристики дорiвнює
. Згiдно з (11.3) зображення iмпульсної характеристики дорiвнює 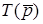 . Тодi
. Тодi
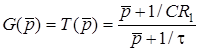 .
.
Для знаходження iмпульсної характеристики 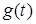 необхiдно знайти оригiнал
необхiдно знайти оригiнал 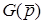 . Безпосередньо оберненим перетворенням Лапласа не користуються, а застосовують табличнi спiввiдношення. Але можуть бути випадки, якi не забезпечено таблично.
. Безпосередньо оберненим перетворенням Лапласа не користуються, а застосовують табличнi спiввiдношення. Але можуть бути випадки, якi не забезпечено таблично.
В даному прикладi степенi полiномiв чисельника i знаменника однаковi, тому доцiльно знизити степiнь чисельника, видiливши цiлу частину. Тодi
 .
.
Згiдно з таблицею оригiналiв матимемо:
 .
.
11.2 Зв'язок мiж часовими та частотними характеристиками
Такий зв'язок встановлюється на основi формули 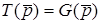 . Вище (лекцiя 8) були наведенi формули (8.1) i (8.7) прямого i оберненого перетворень Лапласа
. Вище (лекцiя 8) були наведенi формули (8.1) i (8.7) прямого i оберненого перетворень Лапласа
 - пряме перетворення;
- пряме перетворення;
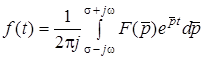 - обернене перетворення.
- обернене перетворення.
Цi спiввiдношення можна записати для iмпульсної характеристики:
 ;
; 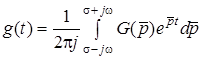 .
.
Оскiльки 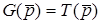 , матимемо
, матимемо
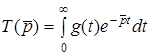 ;
;  . (11.4)
. (11.4)
Для переходу вiд операторних характеристик до частотних зробимо замiну змiнних: 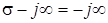 ,
, 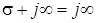 ,
, 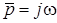 ,
, 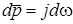 . Тодi (8.1) перетворюється так:
. Тодi (8.1) перетворюється так:
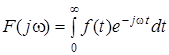 - (11.5)
- (11.5)
пряме однобiчне перетворення Фур'є; а (8.7) перетворюється у
 - (11.6)
- (11.6)
обернене перетворення Фур'є. (Величину j у межах iгноруємо, оскiльки iнтегрування здiйснюється по 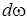 . Iншими словами, за шлях інтегрування при
. Iншими словами, за шлях інтегрування при 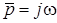 у формулi (11.6) обирається уявна вiсь).
у формулi (11.6) обирається уявна вiсь).
Отже, для всiх тих функцiй, для яких iснує однобiчне перетворення Фур'є (11.5), останнє представляє собою границю, до якої прямує перетворення Лапласа вiд цiєї функцiї, якщо дiйсна частина змiнної  прямує до нуля, тобто
прямує до нуля, тобто 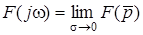 .
.
Тодi при 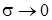 зображення
зображення 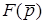 функцiї
функцiї 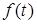 переходить в її комплексну спектральну густину
переходить в її комплексну спектральну густину 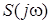
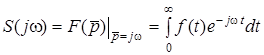 , (11.7)
, (11.7)
операторна передатна функцiя 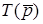 переходить в комплексну передатну функцiю
переходить в комплексну передатну функцiю 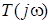 :
:
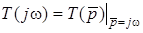 , (11.8)
, (11.8)
а зображення реакцiї 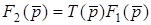 - в комплексну спектральну густину шуканої реакцiї
- в комплексну спектральну густину шуканої реакцiї
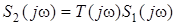 . (11.9)
. (11.9)
Зробимо аналогiчну замiну 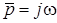 в (11.4):
в (11.4):
 ; (11.10)
; (11.10)
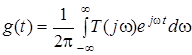 . (11.11)
. (11.11)
Порiвняння (11.10) з (11.7) показує, що 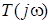 є не що iнше, як комплексна спектральна густина функцiї
є не що iнше, як комплексна спектральна густина функцiї 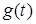 .
.
Отже, часова (iмпульсна) характеристика кола 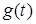 i вiдповiдна їй комплексна передатна функцiя кола
i вiдповiдна їй комплексна передатна функцiя кола 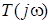 пов'язанi мiж собою парою перетворень Фур'є:
пов'язанi мiж собою парою перетворень Фур'є: 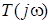 є прямим перетворенням Фур'є для
є прямим перетворенням Фур'є для 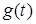 , а
, а 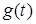 є оберненим перетворенням Фур'є для
є оберненим перетворенням Фур'є для 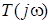 .
.
Цей факт доводить, що iмпульсна характеристика однозначно визначає частотнi характеристики кола i навпаки.
Оскiльки за відомою iмпульсною характеристикою можна знайти перехiдну характеристику, то  також однозначно визначається частотними характеристиками кола.
також однозначно визначається частотними характеристиками кола.
Будь-яка змiна частотних характеристик призводить до вiдповiдної змiни часових характеристик, i навпаки. В найпростiшому випадку частотнi характеристики можуть пропорцiйно змiнюватися, тобто "розтягуватися" або "стискатися" за частотою. "Стискання" АЧХ в a разiв викликає "розтягування" 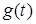 та
та  за часом в те саме число разiв. Iнакше кажучи, чим вужче (ширше) смуга частот, якi пропускаються колом, тим повiльнiше (швидше) протiкають у ньому перехiднi процеси. Для iлюстрування цiєї тези, на рис.11.1 зображено графiки модуля коефiцiєнта передачi за напругою та iмпульсної характеристики послiдовного резонансного контуру для двох значень смуги пропускання (
за часом в те саме число разiв. Iнакше кажучи, чим вужче (ширше) смуга частот, якi пропускаються колом, тим повiльнiше (швидше) протiкають у ньому перехiднi процеси. Для iлюстрування цiєї тези, на рис.11.1 зображено графiки модуля коефiцiєнта передачi за напругою та iмпульсної характеристики послiдовного резонансного контуру для двох значень смуги пропускання (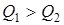 ;
; 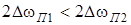 ;
; 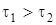 ).
).
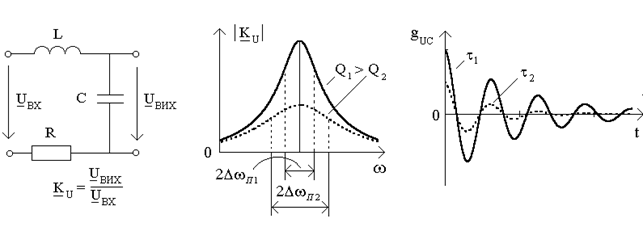
Рисунок 11.1
11.3 Граничнi спiввiдношення мiж часовими та частотними
характеристиками кола
Для оцiнки зв'язку мiж часовими та частотними характеристиками електричних кiл знайдемо також спiввiдношення мiж граничними значеннями часових характеристик (при 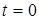 i
i 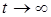 ) i граничними значеннями амплiтудно-частотних характеристик ( при
) i граничними значеннями амплiтудно-частотних характеристик ( при  ;
; 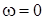 ).
).
У математицi доведено спiввiдношення
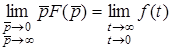 . (11.12)
. (11.12)
Нехай 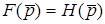 - зображення перехiдної характеристики. Тодi
- зображення перехiдної характеристики. Тодi
 ;
; 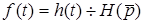 . (11.13)
. (11.13)
Пiдставимо (11.13) до (11.12)
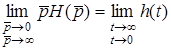 ;
; 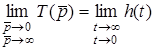 .
.
Як було показано вище, вiд операторної характеристики можна перейти до частотної замiною 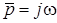 . Тодi матимемо
. Тодi матимемо
 . (11.14)
. (11.14)
На основi формули (11.14) можна записати по двi рiвностi для лiвої та правої частин:
 ;
;  ;
;
 ;
;  .
.
Тодi одержимо
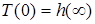 ;
; 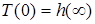 . (11.15)
. (11.15)
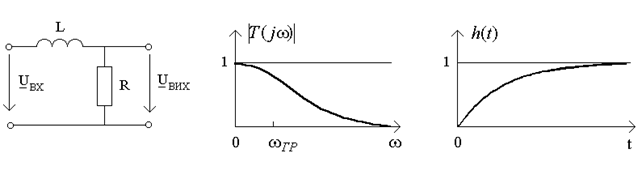
Приклад. Визначимо частотну i часовi характеристики для кола, яке складається з послiдовно з’єднаних iндуктивностi L i опору R. Вважатимемо вхiдну та вихiдну напруги дією та реакцiєю, вiдповiдно (рис.11.2а). Операторна передатна характеристика для цього кола має вигляд:
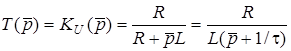 ;
; 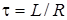 .
.
Комплексна передатна характеристика
 .
.
Амплiтудно-частотна характеристика
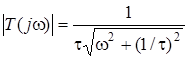 .
.
а) б) в)
Рисунок 11.2
Графiк АЧХ зображено на рис.11.2б. Знайдемо смугу пропускання для даного кола. За визначенням, смуга пропускання - дiапазон частот, на межах якого напруга (струм) або коефiцiєнт передачi зменшується до рiвня 0,707 вiд максимуму. Враховуючи, що для кола першого порядку 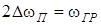 , знайдемо значення
, знайдемо значення  з рiвняння
з рiвняння 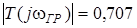 :
:
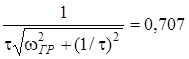 ;
; 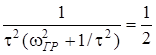 ;
;  .
.
Отже, для кола першого порядку справедливе спiввiдношення, згiдно з яким добуток смуги пропускання на сталу часу є величина постiйна i дорiвнює одиницi. Нагадаємо, що для кола другого порядку цей добуток дорiвнює двом.
Отже, пiдтверджується важливий висновок щодо iснування тісного зв'язку мiж смугою пропускання та сталою часу (тобто мiж часовими та частотними характеристиками).
Визначимо перехiдну характеристику:
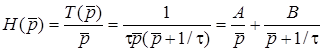 .
.
Скориставшись теоремою розкладання, отримуємо
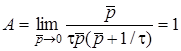 ;
; 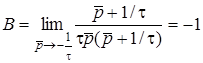 .
.
Тодi 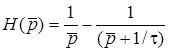 ;
; 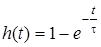 .
.
Графiк перехiдної характеристики зображено на рис 11.2в. Маючи вирази для  i
i 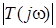 , легко переконатися в слушностi граничних спiввiдношень (11.15):
, легко переконатися в слушностi граничних спiввiдношень (11.15): 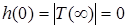 ;
; 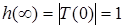 . Цей висновок можна зробити також, аналiзуючи графiки функцiй
. Цей висновок можна зробити також, аналiзуючи графiки функцiй  i
i 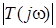 (рис.11.2).
(рис.11.2).
Читайте також:
- Засоби і заходи поліпшення стану виробничого середовища за шумовими характеристиками
- Під впливом форм якого зносу основні фонди стають застарілими за своїми технічними характеристиками і економічній ефективності?
- Соціальний портрет сучасного юриста визначається такими характеристиками.
| <== попередня сторінка | | | наступна сторінка ==> |
| СПОСОБИ ВИЗНАЧЕННЯ ОПЕРАТОРНИХ ФУНКЦIЙ | | | ХАРАКТЕРИСТИКИ ЛАНОК ДРУГОГО ПОРЯДКУ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |