• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

СПОСОБИ ВИЗНАЧЕННЯ ОПЕРАТОРНИХ ФУНКЦIЙ

Iснує кiлька способiв визначення операторних функцiй. Перед тим, як їх розглянути, зробимо кiлька попереднiх зауважень.

1. Операторна передатна функцiя не залежить вiд вигляду дії, а тiльки вiд параметрiв кола.

2. Оскiльки справедливi закони теорiї кiл в операторнiй формi, можна не складати диференцiйних рiвнянь, а обмежитись алгебраїчними рiвняннями.

Перший спосiб. Визначення операторної функцiї за законами Ома i Кiрхгофа в операторнiй формi.

Знайдемо операторний коефiцiєнт передачi за напругою на прикладi схеми (рис.10.1а). Згiдно з визначенням .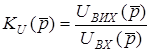

а) б)

Рисунок 10.1

Нехай 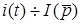; ; 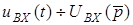. Тодi слушнi спiввiдношення: ; . Вхiдний опiр кола становить: .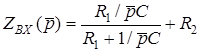

Пiдставивши вирази для зображень напруг до формули , матимемо:

.

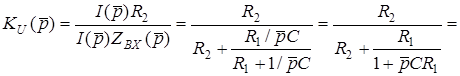
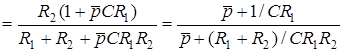Визначимо сталу часу для даного кола. Для цього розглянемо схему в режимi вiльних коливань, тобто коли джерело е.р.с. замкнено. Тодi еквiвалентний опiр кола вiдносно ємностi становить 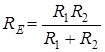(рис.10.1б).

Отже, 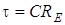. Тодi вираз для матиме вигляд:

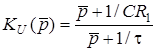. (10.1)

Якщо коло складніше, використовують потужнiші способи, наприклад, метод вузлових напруг.

Другий спосiб. Визначення операторної функцiї за допомогою методу вузлових напруг.

Розглянемо ЛЕК, яку зображено на рис.10.2а. Нехай загальна кiлькiсть вузлiв у колi дорiвнює M. Оскiльки один вузол (M-й) заземлюється, кiлькiсть незалежних вузлiв дорiвнює n = M-1.

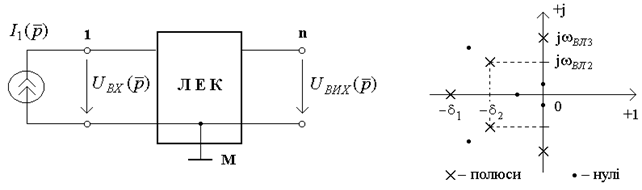
а) б)

Рисунок 10.2

Знайдемо операторний коефiцiєнт передачi за напругою

.

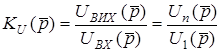За методом вузлових напруг формула для розрахунку вузлової напруги має вигляд

. (10.2)

В операторнiй формi (10.2) можна записати

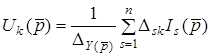, (10.3)

де [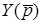] - операторна матриця провiдностей;

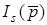- операторнi вузловi струми, s = 1,2, ... k, ... n.

Операторна матриця 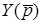складається вiдповiдно до схеми ЛЕК:

.

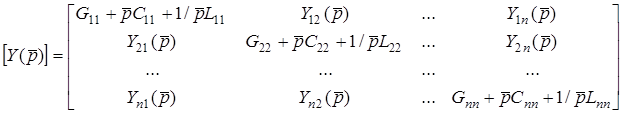Дiагональний елемент - це арифметична сума операторних провiдностей всiх тих елементiв, якi з’єднані з вузлом з номером k. Якщо , то 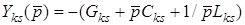- провiднiсть вiтки, яка увiмкнена мiж k-м та s-м вузлами.

Для лiнiйних електричних кiл , тобто матриця операторних провiдностей симетрична вiдносно головної дiагоналi.

Нехай на входi кола дiє джерело струму 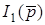, (тобто s = 1). Викори-стовуючи матрицю , за формулою (10.3) розрахуємо вузловi напруги

; . (10.4)

Тодi

. (10.5)

Розрахувавши вiдношення алгебраїчних доповнень матрицi , якi входять до формули (10.5), отримаємо вiдношення полiномiв чисельника 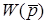та знаменника 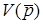, кожний з яких мiстить тiльки цiлi степенi аргументу :

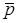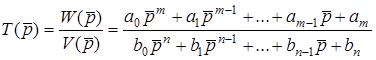. (10.6)

З формули (10.5) виходить, що операторна передатна функцiя є дробовою рацiональною функцiєю (ДРФ) з дiйсними коефiцiєнтами. ДРФ звуться функцiї виду (10.6) комплексної змiнної . ДРФ можна визначити ще, як вiдношення полiномiв i 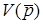з дiйсними коефіцієнтами. Цi коефiцiєнти 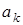i - дiйснi числа, тому що вони є добутком провiдностей.

Функцiя (10.6) зветься правильною, якщо степiнь полiнома чисельника нижчий степеня полiнома знаменника (m < n). Найбiльше з чисел m i n характеризує порядок функцiї.

Якщо винести коефiцiєнти 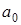i , то полiноми 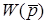i 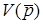можна розкласти на добутки m(n) лiнiйних спiвмножникiв, тобто податити 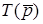у виглядi:

. (10.7)

де 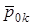- коренi полiнома чисельника, або нулi функцiї ;

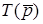- коренi полiнома знаменника, або полюси функцiї .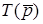

Оскiльки коефiцiєнти 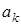i 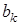- дiйснi числа, то комплекснi коренi полiномiв чисельника i знаменника можуть зустрiчатися лише спряженими парами (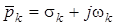i ). Коренi чисельника i знаменника можна показати на комплекснiй площинi. Зображення нулiв та полюсiв операторної функцiї на комплекснiй площинi зветься картою нулiв та полюсiв (рис.10.2б).

10.1 Зв'язок мiж операторною характеристикою i диференцiйним

рiвнянням кола

Електричне коло, як вiдомо, можна описати диференцiйним рiвнянням, яке має вигляд

. (10.8)

Вважатимемо, що 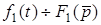; . Тодi, вiдповiдно до теореми диференцiювання, можна записати

;

;

;

.........................................................

.

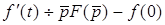Переведемо рiвняння (10.8) до простору зображень. При цьому в останньому рiвняннi позначимо суму похiдних як деякий полiном 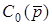; якщо , то ; якщ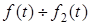о , то 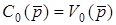. Тодi

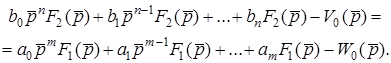(10.9)

Перетворимо рiвняння (10.9)

;

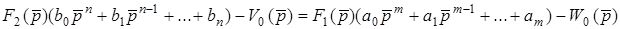або 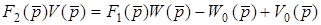, (10.10)

де 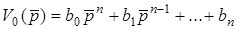- характеристичний полiном.

З (10.10) можна отримати вираз для :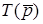

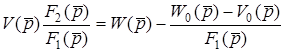, звiдки матимемо

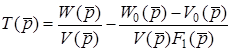. (10.11)

Для реального кола при , 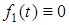(перше лапласiвське обмеження). Отже, при повинна дорiвнювати нулю також функцiя . Щоб в рiвняннi (10.10) при , необхiдно виконати умову

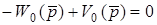. (10.12)

Оскiльки 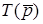визначається за нульових початкових умов, формула (10.12) буде справедлива. Тодi з (10.11) отримуємо

,

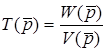де 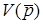- характеристичний полiном (або полiном Гурвiца).

Висновок. Передатна функцiя 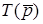однозначно пов'язана з параметрами ЛЕК. До знаменника операторної функцiї будь-якого стiйкого електричного кола входить полiном з дiйсними коефiцiєнтами 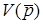, який зветься характеристич-ним полiномом або полiномом Гурвiца. Полюси 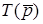знаходяться серед коренiв характеристичного рiвняння, що відповідає диференцiйному рiвнянню (10.8).

Полiном 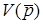має характернi ознаки: 1) 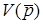вiдповiдає режиму вiльних коливань; 2) всi коренi полiнома Гурвiца повиннi знаходитись у лiвiй пiвплощинi; 3) 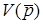мiстить всi степенi 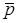, причому коефiцiєнти при степенях 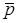або всi додатнi, або всi вiд'ємнi.

Отже, аби отримати характеристичне рiвняння, треба записати 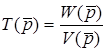та прирiвняти знаменник 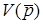до нуля. Наприклад, для кола (рис.10.1а) ; ; .

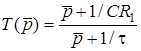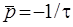Для отримання характеристичного рiвняння можна також скористатись вхiдними операторними функцiями. Якщо вхідною дією є напруга, треба прирiвняти до нуля вхiдний опiр ; якщо дією є струм, то треба розв'язати рiвняння .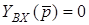

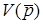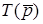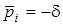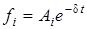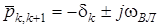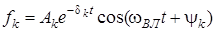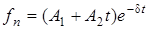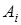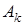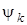
Принагiдно нагадаємо, що характер вiльних коливань у колi залежить вiд вигляду коренiв (полюсiв ). Кожному простому дiйсному кореню (полюсу) вiдповiдає доданок ; кожнiй парi простих комплексно-спряжених полюсiв вiдповiдає доданок . Для кратних полюсiв (наприклад, другого степеня кратностi) можна записати . У цих виразах коефiцiєнти , , , 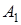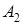- дiйснi константи.

Наприклад, картi полюсiв (рис.10.2б) вiдповiдає коливання, яке описується функцiєю (всi коренi простi):

.

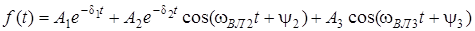Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
7. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
8. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
9. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
10. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
11. Біологічні способи лікування ран.
12. Біостратиграфічні методи визначення віку порід

Переглядів: 1081