• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Афінний шифр k-ro порядку.

Ключ: АGL_k(Z_n) і S GL_k().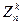

Шифрування. Повідомлення розбивається на k-грами. Кожна k-грама X заміщується k-грамою Е(Х) = АХ + S¹

Дешифрування. Кожна k-грама X’ криптотексту заміщується k-грамою D(X') = А'X’ + S’, де А' = А^-1 і S' = -A'S — дешифруючий ключ.

Приклад 3.6. Хочемо зашифрувати повідомлення завтра за допомогою ключа 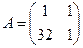i 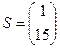на Z₃₃.

Частина роботи вже виконана нами у прикладі 3.4. Після розбиття повідомлення на вектори-біграми і множення їх на матрицю А за модулем 33 ми були отримали 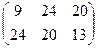додаємо до кожного стовпчика S і отримуємо 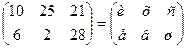тобто криптотекст иехвсш.

Знайдемо також дешифруючий ключ. У прикладі 3.4 була отримана матриця 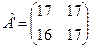. Обчислюємо

3.3. Криптоаналіз. Атака з вибором відкритого тексту. Нескладно зауважити, що афінний шифр нестійкий до цього виду криптоаналізу. Позначимо через Х_і, 1 і k, вектор з k-тою компонентою 1 і з рештою компонент, що дорівнюють 0, а через Х₀ нульовий вектор. Суперникові досить довідатись, в які криптотексти переходять відповідні цим векторам
k-грами. Справді, E(X₀) = S, а образ Е(Х_і) рівний k-тому стовпчику матриці А, що дозволяє повністю визначити ключ.

Атако з відомим відкритим текстом. Спочатку покажемо, що лінійний шифр вразливий від такої атаки. Припустимо суперник знає, що шифруюче відображення Е(Х) = АХ перетворює вектори X1,..., Xk у вектори X’1,..., X’k. Сформуємо із стовпчиків X1,..., Xk матрицю М, а із стовпчиків X’1,..., X’k матрицю С. Як неважко зро зуміти, С = AM і М = А'С'. Якщо матриця С оборотна, то звідси зразу можна визначити дешифруючий ключ А' = МС^-1. Якщо суперникові пощастить менше і матриця С виявиться необоротною, то він не зможе визначити А’

однозначно. Однак кількість можливостей може зменшитись настільки, що А’ вдасться знайти після деякого перебору.

Для афінного шифру Е(Х) = АХ + S необхідно знати на одну пару (Х,Х'), де X’ = Е(Х), більше. Віднявши рівність АХ + S = X’_і від кожної з рівностей АХ_і + S = Х’_і ,i k, ми зведемо задачу визначення дешифруючого ключа до попереднього випадку.

Приклади такого криптоаналізу винесені у вправи 3.8-3.13. Атака лише за криптотекстом. Афінний шифр 2-го порядку піддається частотному аналізу як і будь-який біграмний шифр. Якщо порядок k дещо збільшити, частотний метод перестане працювати.

Розглянемо лінійний шифр k-ro порядку над алфавітом Z_n. Подивимось, які перспективи може мати брутальна атака, іншими словами, наскільки реально влаштувати повний перебір ключів. Очевидно, кількість ключів дорівнює кількості матриць в GL_k(Z_n), для якої в пункті 2.5 було введено позначення ф_к(n). Там же була виведена її формула. З одного боку видно, що ф_к(n) 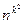З іншого, порівнюючи із формулрю для функції Ойлера ф(п) = ф₁(п), отримуємо ф_к(n) ( ф(п))^к. 3 використанням твердження 2.15 маємо оцінку ф_к(n) 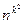/(6lnlnn)^k при п > 4. Асимптотичне, значення ф_к(n) зростає за п як поліном і за k як експоненційна функція. Отримана оцінка дозволяє оцінити розмір простору ключів для будь-яких конкретних k і п (див. також вправу 3.20). Як видно, перебір ключів напевне є нереальним скажімо при
k = 5, п = 32. Платою за збільшення порядку шифру є збільшення часу криптування і декриптування.

ВПРАВИ

3.1. Для монограмного афінного шифру перевірити співвідношення D(E(x)) = х, де х — довільний елемент із Z_n

3.2. а) Зашифрувати за допомогою афінного шифру з ключем а = 4,
s —повідомлення ні, записане українською абеткою із 33 літер.

b) Знайти дешифруючий ключ і розшифрувати криптотекст дкцзьи, отриманий за допомогою того ж шифру з тим же ключем.

3.3. а) Каналом зв'язку передаються повідомлення, закриптовані за допомогою монограмного лінійного шифру, причому використовується 35-символьний алфавіт, у якому під номерами від 0 до 32 йдуть літери української абетки, пропуск має номер 33, а крапка — 34. Частотний аналіз показав, що у потоці криптотекстів найчастіше зустрічається літера Щ. Опираючись на факт що найпоширенішим символом в україномовних текстах є пропуск, знайти дешифруючий ключ і розшифрувати криптотекст

ТЬЕПЩЧАЕОЧИЬЯЩЕ ЛЕАМЮАФ.ҐЮОЩХАЄ ЕЯ

Знайти шифруючий ключ і закриптувати повідомлення

КРЕВЕТКИ ЗАКІНЧИЛИСЬ.

b)Повідомлення криптуються з використанням того ж шифру, але використовується
33-символьний алфавіт, в якому лише літери української абетки. Згідно з результатами частотного аналізу, у потоці криптотекстів найчастіше зустрічається літера Ф. В числі інших перехоплено крипто текст УФЇЄФГШХАЙХФ. Розшифрувати його, опираючись на факт, що найпоширенішою літерою в україномовних текстах є О. Знайти шифруючий ключ і закриптувати повідомлення ЗАВЕРШУЙТЕ.

c)Використовується той же шифр, але над 36-символьним алфавітом. Першими символами алфавіту є крапка, кома та пропуск, які мають номери 0, 1 та 2 відповідно. Номери від 3 до 35 належать літерам української абетки. Відомо, що у потоці криптотекстів найчастіше зустрічаються літери Є і Ь, саме в такому порядку. Виходячи з того, що найпоширенішими в україномовних текстах є пропуск і літера О, знайти дешифруючий ключ і розшифрувати криптотекст ЬЛКШРЄИЄҐЯЇВЖҐЗИЄГФШЬЯЖ.ЄНЇН. Знайти шифруючий ключ і закриптувати повідомлення ЗАБУДЬ УСЕ, БОБЕ.

3.4. а) Каналом зв'язку передаються повідомлення, написані у 33-літерному українському алфавіті без пропусків і знаків пунктуації, і закриптовані за допомогою монограмного афінного шифру. Відомо, що у потоці криптотекстів найчастіше зустрічаються літери У і 0, саме в такому порядку. Виходячи з того, що найпоширенішими літерами української абетки є 0 і Н, знайти дешифруючий ключ і розшифрувати криптотекст ЗУКУОН. Знайти шифруючий ключ і закриптувати повідомлення ЗАГАСИТИ.

b) Повідомлення написані англійською мовою у 26-літерному алфавіті без пропусків і розділових знаків, і закриптовані за допомогою монограмного афінного шифру. Відомо, що у потоці криптотекстів найчастіше зустрічаються літери 0 і Н, саме в такому порядку. Виходячи з того, що найпоширенішими літерами англійської абетки є Е і Т, знайти дешифруючий ключ і розшифрувати криптотекст HSFOSЬPSHHSFO. Знайти шифруючий ключ і закриптувати повідомлення NOQUESTIONS.

3.5. а) Довести, що афінне відображення однозначно представляється у вигляді композиції лінійного відображення та зсуву.

b)Довести, що афінний шифр утворює групу (кількість букв у алфавіті відкритого тексту п фіксована).

3.5. а) До матриці А = знайти обернену Zn

b)Використовуючи матрицю А як ключ, закриптувати за допомогою лінійного шифру
2-го порядку повідомлення ПРОЩАЙ .

c)Використовуючи в якості ключа ту ж матрицю А і вектор S = , закриптувати те ж повідомлення за допомогою афінного шифру.

d) Знайти дешифруючий ключ і дешифрувати криптотекст ЛЩЯЛЧОРХ, отриманий за допомогою афінного шифру з ключем як у попередньому пункті.

3.6. а) Суперник знає, що Аліса та Боб листуються українською мовою і криптують свою кореспонденцію за допомогою лінійного шифру 2-го порядку. При цьому використовується
34-символьний алфавіт, де номери від 0 до 32 належать літерам української абетки, а 33-тім символом є пропуск. Суперникові вдалося підслухати повідомлення Аліси Бобові: ҐТІШГҐРЮІДЖСМАЧДИКЯ ЄЦЖС . Він здогадався, що останнім словом у повідомленні е підпис відправника АЛІСА. Виходячи з цього припущення, знайти дешифруючий ключ і розшифрувати криптотекст. Знайти шифруючий ключ і закриптувати повідомлення ЧЕКАЮ БІЛЯ ФОНТАНУ БОБ

b)У тій же ситуації, що й в попередньому пункті, суперник перехопив криптотекст ДТЛРНІЇРЦДЄЙМЗЧОТШБЕ. Цього разу суперник здогадався, що повідомлення починається звертанням БОБЕ. Розшифрувати криптотекст, виходячи з цього припущення. Знайти шифруючий ключ і закриптувати таке ж, як і в попередньому пункті, повідомлення ЧЕКАЮ БІЛЯ ФОНТАНУ БОБ

3.7. а) Використовується 26-літерний англійський алфавіт, занумерований числами від 0 до 25. Пропуски між словами ігноруються. Статистичний аналіз показав, що в потоці криптотекстів найчастіше зустрічаються біграми VO і IT. Припустимо, що в англомовних текстах на тему, яка обговорюється в повідомленнях, найчастіше зустрічаються біграми ТН і НЕ. Знайти дешифруючий ключ і розшифрувати повідомлення ITEJASVOQOXT

3.10. а) Повідомлення шифруються лінійним біграмним шифром над 30-символьним алфавітом, в якому номери від 0 до 25 займає латинська абетка, а пропуск, апостроф, кома і крапка, саме в такому порядку, мають номери 26-29. Статистичний аналіз великого масиву криптотекстів показав, що найчастіше трапляються біграми ЕІ і QQ. Припустимо, що вони відповідають найпоширенішим в англійській мові біграмам Е_ і S_ цього алфавіту. Встановити дешифруючий ключ і розшифрувати криптотекст LHV,QQQW HESLSEIWYRVGYQ ЬRЬC

b)Відомий розвідник користується біграмним лінійним шифром над 34-символьним алфавітом, у який входять українські літери (0-32) і пропуск (33). Втім, щоб ускладнити криптоаналіз, досвідчений розвідник при шифруванні ігнорує всі пропуски між словами (таким чином, у відкритому тексті немає пропусків, але у криптотексті вони можуть з'явитись. Суперник перехопив повідомлення ОЩРФНААИЗЖЕБ ЗПЗ розвідника в центр і здогадався, що останні п'ять символів криптотексту відповідають підпису відправника ІСАЄВ. Провести дешифрування.

3.11. а) Перехоплено криптотекст ЮВЧРУЗІНДШЛЗТАЬВБЯІТЬГКЇ , отриманий за допомогою лінійного біграмного шифру над 33-літерним алфавітом (пропуски між словами ігноруються). Відомо, що повідомлення закінчується підписом відправника НАТАЛКА. Знайти дешифруючий ключ і прочитати повідомлення.

b) Перехоплено криптотекст ШЩЄВЛОІІЩШАФУАРЇАБННЕЮ , отриманий за допомогою лінійного біграмного шифру над 34-символьним алфавітом, у який входить українська абетка (0-33) і пропуск (33). Відомо, що повідомлення закінчується підписом відправника _ВАНГА. Знайти дешифруючий ключ і прочитати повідомлення

3.13. (За [111]) Перехоплено повідомлення

ЕЬЩИЦЕППІДНПТЛЧТХХИШХКПСҐТНВТУ

отримане за допомогою лінійного шифру 3-го порядку над 33-літерним алфавітом (пропуски між словами ігноруються). Повідомлення закінчується підписом відправника ДЖЕЙМСБОНД, що дає можливість встановити відповідність між трьома триграмами повідомлення і криптотексту. Знайти дешифруючий ключ і прочитати повідомлення.

3.14. а) Для лінійного шифру k-ro порядку над алфавітом Zn довести, що композиція шифруючих відображень з ключами А, В Є M_k(Zn)* (спочатку шифрування з ключем А, а потім з В) також є шифруючим відображенням з ключем В А.

b)Довести, що лінійний шифр k-ro порядку над алфавітом Zn утворює групу, ізоморфну групі Mk(Zn)*

3.15.Виконати вправу 3.5 для афінного шифру k-ro порядку. Чисельні підрахунки у пункті с провести при k = 2.

3.16.Розглянути лінійне шифруюче відображення Е : 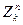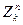, задане формулою
Е(Х) = АХ з А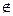Mk(Zn)*. Довести, що

a)кожна біграма з E(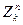) має щонайменше два прaобрази;

b)кожен криптотекст, отриманий шифруванням деякого повідомлення довжини km, можна розшифрувати щонайменше 2^m способами.

3.17.([111]) Нехай неодинична матриця А з M₂(Z_n) використовується як ключ для лінійного біграмного шифру Е в n-символьному алфавіті. Нерухомою біграмою шифруючого відображення Е назвемо таку біграму (вектор) X, що Е(Х) = X.

а) Знайти умову на матрицю А, за якої існує єдина нерухома біграма, а саме аа =

ЛЕКЦІЯ 8

Читайте також:

1. Бінарне відношення порядку.
2. Відбулися кардинальні зміни у світовому порядку. На авансцену виходить Європа1.
3. Гарантії законності - умови суспільного життя і заходи, що приймаються державою для забезпечення режиму законності і стабільного правопорядку.
4. Динамічна інтерпретація диференційного рівняння другого порядку. Консервативні системи.
5. Загальна характеристика нарядів по охороні громадського порядку.
6. Застосування геометричних перетворень для побудови ліній другого порядку.
7. Застосування інваріантів для побудови ліній другого порядку.
8. Злочини проти міжнародного правопорядку.
9. Лекція №18. Лінійні диференціальні рівняння першого порядку. Рівняння в повних диференціалах
10. Ліквідація бюджетних організацій здійснюється ліквідаційною комісією, створеною за рішенням уповноваженого органу в загальноприйнятому порядку.
11. Підстави для скасування і зміни судового рішення у касаційному порядку.

Переглядів: 5805