• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад.Розглянемо відповідність, зображена на мал. 1.7

□ Відповідність f є функціональною, тобто функцією. З того, що вона всюди визначена виходить, що f – відображення. Відповідність не є сюр’єктивною (елемент d не має прообразу в множині Х). Отже, відповідність f є відображенням множини Х у множину Y, тобто .■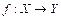

Приклад.Розглянемо відповідності :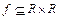

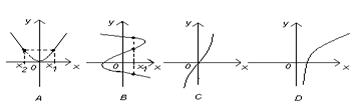
□ Дамо характеристику властивостей відповідностей.

A –відповідність f усюди визначена: ; не сюр’єктивна тому, що , тобто 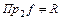; функціональна, тому що образом будь-якого елемента є єдиний елемент ; є відображенням множини R у множину R , тому що вона всюди визначена і функціональна; відображення не є ін’єктивним, тому що існують елементи , для яких f(x₁)=f(x₂)=у; відображення не є бієктивним, тому що воно не є сюр’єктивним і ін’єктивним.

B – відповідність f усюди визначена: ; сюр’єктивна, бо ; не функціональна, оскільки існує 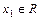, для якого f(x₁)=y₁, f(x₁)=y₂, f(x₁)=y₃.

C – відповідність усюди визначена: ; сюр’єктивна: ; функціональна: образом будь-якого елемента з області визначення є єдиний елемент із області значень відповідності; взаємно однозначна, тому що вона всюди визначена, сюр’єктивна, функціональна й прообразом будь-якого елемента з області значень є єдиний елемент із області визначення відповідності; є відображенням R на R, тому що повністю визначена й сюр’єктивна; відображення ін’єктивно, тому що для будь-яких різних елементів х з області визначення їхні образи y = f(x) також різні; відображення бієктивно, тому що воно є одночасно сюр’єктивним і ін’єктивним, тобто відображення є взаємно однозначним відображенням.

D – відповідність f є частково визначеною, тому що ; сюр’єктивною, тому що ; функціональною, бо образом будь-якого елемента з є єдиний елемент із ; відображенням не є тому, що відповідність не є всюди визначеною.■

Відповідність q^–1=(Y,X,Q ^{– 1}), Q ^{– 1}, називають оберненоюдля відповідності q=(X,Y,Q), Q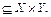

Якщо відповідність, обернена до функції f, є функціональною, то вона називається функцією, оберненою до f, і позначається f ^{– 1} .

Для функції f обернена функція існує тоді й тільки тоді, коли f є взаємно однозначною відповідністю між своєю областю визначення і областю значень.

Приклад.□ Різні види кодування (кодування букв абеткою Морзе, подання чисел у різних системах числення, секретні шифри, вхідні і вихідні номери в діловій переписці й т.д.) є відповідностями між об'єктами, що кодуються, і кодами, що об’єктам привласнюються. Ці відповідності, як правило, мають всі властивості взаємно однозначної відповідності, крім, можливо, одного - сюр’єктивності. Одиничність образа й прообраза в кодуванні гарантує однозначність шифровки й дешифрування. Відсутність сюр’єктивності означає, що не кожний код має сенс. Наприклад, кодування телефонів шестизначними номерами не сюр’єктивне, оскільки деякі номери ніяким телефонам не відповідають. Для кодувальної функції, яка кожному об'єкту зі своєї області значень ставить у відповідність деякий код, зворотною буде декодувальна функція, яка кожному коду ставить у відповідність закодований цим кодом об'єкт. Якщо кодувальна функція не сюр’єктивна, то декодувальна функція не всюди визначена. ■

Композиція функцій (підстановка функції f в g) :, g : - це функція якщо h(x) = g(f (x)), де

Приклад.□ а) Є множина {1,2,3} і її перетворення: , 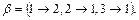Для завдання перетворення кінцевих множин можна використовувати наступний запис: , 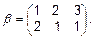Композиція перетворень є нове перетворення: ,

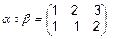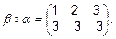
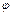
б) Множина K =команд ЕОМ відображається в машинні коди, тобто в натуральні числа. За допомогою суперпозиції кодувальної функції , і арифметичних функцій виявляються можливими арифметичні дії над командами (які самі по собі числами не є), тобто функції , і т.д. ■

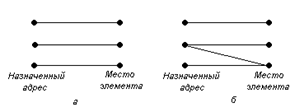
Приклад.□ Граф адресного дешифрування: а – випадок справної схеми; б – випадок з несправністю Рис. 1.8

При діагностуванні мікросхем напівпровідникової пам'яті роботу дешифратора адреси можна представити у вигляді графа адресного дешифрування, що показує відповідність між адресами й елементами пам'яті. При правильній роботі є взаємно однозначна відповідність (мал. 1.8а). При несправності дешифратора спостерігається порушення взаємне однозначної відповідності в графі адресного дешифрування (мал.1.8б). ■

=================== «» ====================

§ 3. Поняття алгебри. Алгебра множин Кантора

Алгеброю А називається сукупність множини М с заданими в ньому операціями S = { f₁, f₂,…,f_п}, тобто

А = <M, S >,

де М – носій алгебри , S – сигнатура алгебри, що містить у собі одномісні, двомісні й інші операції.

Алгебра виду A = <M, f>, де f – двомісна операція, називається групоїдом.

Якщо f – операція типу множення (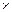), то групоїд називається мультиплікативним. Якщо f – операція типу додавання (+), то групоїд називається адитивним.

Елемент е називається нейтральним елементом групоїда А, якщо для будь-якого елемента 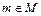виконується рівність

m f е = е f m = m.

Якщо групоїд A = <M ,f > мультиплікативний, то нейтральний елемент називається одиницею й позначається через 1, якщо адитивний, то нейтральний елемент називається нулем і позначається через 0.

Якщо множина М містить нейтральний елемент е щодо операції f , то елемент n називається зворотним елементу m , якщо

m f n = n f m = e.

Запис 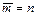означає, що зворотним елементом елементу m є елемент n. При адитивному запису зворотний елемент елементу m позначається через – m, а при мультиплікативному записі – через m ^{– 1} .

Групоїд A = <M, f > називається ідемпотентним, якщо його сигнатура задовольняє закону ідемпотентності, тобто для будь-якого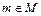

m f m = m.

Групоїд A = <M, f > називається комутативним або абелевим, якщо його сигнатура підкоряється закону комутативності, тобто для будь-яких m,n

m f n = n f m.

Групоїд A = <M, f > називається асоціативним або напівгрупою, якщо його сигнатура задовольняє закону асоціативності, тобто для будь-яких

(m f n) f p = m f (n f p).

Напівгрупа A = <M, f >, у якій здійсненні зворотні операції, називається групою.

Приклад.До якого типу ставиться алгебра A = < Z ,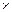>, що є сукупністю множини цілих чисел із заданою в ній операцією множення.

□ У множині цілих чисел виконується комутативний закон. Виходить, заданий мультиплікативний групоїд є комутативним або абелевим. У даній множині також виконується закон асоціативності. Отже, заданий групоїд є асоціативним або напівгрупою. Інакше кажучи, заданий мультиплікативний групоїд є абелевою напівгрупою по множенню.

Нейтральним елементом е є 1, тобто е = 1, тому що для будь-якого цілого числа m виконується умова mּ1=1ּт = m.

Для будь-якого цілого числа m зворотним елементом m ^{– 1} буде 1/m, тому що mּּm = e = 1. Тому що групоїд є напівгрупою і у ній здійсненна зворотна операція, то він є групою. Таким чином, задана алгебра є абелевою групою по множенню. ■

========= «» ========

Переглядів: 788