• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Способи задання бінарних відношень

Теоретичні основи

§ 4. БІНАРНІ ВІДНОШЕННЯ

Бінарне відношення R у множині М - це підмножина його квадрата: 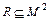, де .

Елементи перебувають у відношенні R, якщо 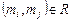, 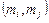- кортеж.

1. Матриця суміжності – це матриця ,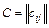

Приклад.Задано блок-схему ЕОМ, запропоновану фон Нейманом, що складається із множини пристроїв М={a,b,c,d,e}, де a – пристрій введення, b – процесор (арифметичний пристрій), c – пристрій керування, d – запам'ятовувальний пристрій, e – пристрій виводу. Якщо із пристрою m_i надходить інформація в пристрій т_j ,то ці пристрої перебувають у відношенні R, під яким розуміється інформаційний обмін між цими пристроями. Задати відношення R у вигляді матриці суміжності.

□ Матриця суміжності має вигляд

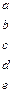
Множина отриманих кортежів визначає відношення

R = {(a,b),(a,c),(a,d ),(b,c),(b,d ),(b,e),(c,a),(c,b),(c,d ),(c,e),(d,b),(d,c),(d,e), (e,c)}.

Відношення R підмножина множини М, тобто , що погоджується з визначенням бінарного відношення.

2. Граф - сукупність множини М з заданим у ньому бінарним відношенням 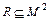, G = <M, R> , де М – носій графа (множина вершин); R – сигнатура графа (множина дуг).

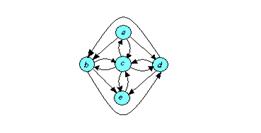Приклад.Побудувати граф G=<M,R>, що задає відношення R з попереднього прикладу.

□ Шуканий граф показаний на мал. 1.9 : Рис. 1.9

Тут вершинами графа (кружки або точки) є елементи множини М={a,b,c,d,e}, тобто пристрою ЕОМ. Дуги (стрілки) указують напрямок потоку інформації. При цьому, як 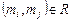, то вершина 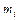- початок дуги, а вершина 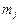- кінець дуги. ■

Читайте також:

1. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
2. Біологічні способи лікування ран.
3. Валютний курс і способи його визначення
4. Варіанти і способи вимірювань характеристик телефонних каналів
5. Вибір кращих альтернатив за допомогою бінарних відношень
6. Види і способи вибіркового спостереження.
7. Види середніх величин та способи їх обрахування.
8. Види середніх величин та способи їх обрахування.
9. Види середніх і способи їх обчислення
10. Види та способи гартування.
11. Види та способи здійснення посягань на територіальну цілісність.
12. Види цивільно-правових договорів в “Руській Правді”, способи їх укладення.

Переглядів: 2100