
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Фактор – множина
Окіл одиничного радіусу елемента 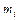
 - множина елементів
- множина елементів 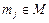
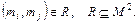
Фактор–множина множини М по відношенню R- множина околів одиничного радіуса, узятих для всіх елементів з М при заданні в ньому відношення  Фактор–множина повністю визначає відношення R.
Фактор–множина повністю визначає відношення R.
Приклад.Задати бінарне відношення з розглянутого приклада у вигляді фактор - множини.
□ Фактор – множина будується у вигляді двох рядків Тоді другий рядок задає фактор – множина М по R:
a b c d e
{b,c,d}{c,d,e}{a,b,d,e} {b,c,e}{c}. ■
4. Перерахування дуг графа ( множина впорядкованих пар )
Приклад.□ Для розглянутого приклада будемо мати: М={a,b,c,d,e}, R={(a,b), 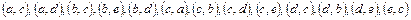 }.
}.
 Властивості бінарних відношень
Властивості бінарних відношень
1. рефлексивне , якщо для 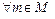 справедливо
справедливо 
У матриці суміжності на головній діагоналі знаходяться одиниці.
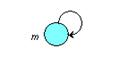
У графі кожний елемент (вершина) має петлю – дугу виду (т,т):
2. анти рефлексивне, якщо для  справедливо
справедливо 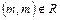 ,
,
 У матриці суміжності на головній діагоналі знаходяться нулі. У графі немає жодної петлі.
У матриці суміжності на головній діагоналі знаходяться нулі. У графі немає жодної петлі.
3. симетричне, якщо для 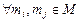 з умови
з умови 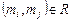 виходить
виходить  ,
,  . Матриця суміжності симетрична щодо головної діагоналі. У графі будь-яка пара вершин зв'язана двома протилежно спрямованими дугами:
. Матриця суміжності симетрична щодо головної діагоналі. У графі будь-яка пара вершин зв'язана двома протилежно спрямованими дугами:
4. антисиметричне: для 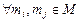 з умов
з умов 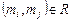 і
і  виходить, що mi=mj або обидва відношення
виходить, що mi=mj або обидва відношення 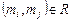 й
й  виконуються одночасно тільки тоді, коли тi=mj. Матриця суміжності несиметрична. У графі можуть бути петлі, але зв'язок між вершинами, якщо він є, відображається тільки одною дугою.
виконуються одночасно тільки тоді, коли тi=mj. Матриця суміжності несиметрична. У графі можуть бути петлі, але зв'язок між вершинами, якщо він є, відображається тільки одною дугою.
5. асиметричне (несиметричне), якщо для 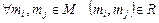 й
й  взаємно виключаються, тобто якщо
взаємно виключаються, тобто якщо 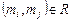 , то
, то 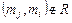 й навпаки.
й навпаки.
Матриця суміжності несиметрична з нульовими елементами на головній діагоналі. У графі петлі відсутні, а вершини можуть бути зв'язані тільки одною дугою. Якщо відношення асиметрично, то воно й антирефлексивне.
 6. транзитивне, якщо для
6. транзитивне, якщо для 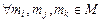 з умов
з умов 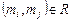 і
і  виходить, що
виходить, що  .
.
У графі для всякої двійки дуг таких, що кінець першої збігається з початком другої, існує третя дуга, яка має загальний початок з першою й загальний кінець із другою дугою. Цю дугу називають транзитивно замикаючою дугою.
§ 5. БІНАРНЕ ВІДНОШЕННЯ ЕКВІВАЛЕНТНОСТІ
Поняття “відношення еквівалентності”, “ фактор-множина“, “класи еквівалентності” використовуються при побудові математичної моделі деякої реально функціонуючої складної системи. З формальної точки зору модель є якась фактор - множина елементів об'єкта моделювання щодо деякого відношення еквівалентності, заданого на вихідній системі. При дослідженні виникає задача вибору істотних властивостей, деталей, ознак об'єкта моделювання. Відношення еквівалентності, з одного боку, ототожнює другорядні, несуттєві ознаки й властивості, і, з іншого боку - виділяє як представників класів еквівалентності основні властивості. Якщо об'єкт моделювання представлений у вигляді композиції елементів деякої базисної множини, то питання про співвідношення моделі і її прообразу дозволяється на основі інформації про елементи, на яких уводиться відношення еквівалентності - або це самі елементи базисної множини, або деякі підмножини елементів, або підмножини множини підмножин елементів.
 Бінарне відношення R у множині М, яке є рефлексивним, симетричним й транзитивним, називають відношенням еквівалентності і позначають ~ , тобто для
Бінарне відношення R у множині М, яке є рефлексивним, симетричним й транзитивним, називають відношенням еквівалентності і позначають ~ , тобто для  має місце:
має місце:
1. кожний елемент еквівалентний сам собі: x ~ x ;
2. якщо х еквівалентний y, то й y еквівалентний х: якщо х ~ y, те y ~ х;
3. якщо х еквівалентний у, а у еквівалентний z , то х еквівалентний z: якщо х ~ y, а y ~ z , то х ~ z .
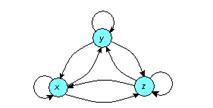
Відношення еквівалентності ілюструється графом з петлями, кожна пара вершин зв'язана двома протилежно спрямованими дугами, які утворюють транзитивно замикаючі дуги :
Клас еквівалентності K (т) елемента т - множина всіх елементів mi , кожний з яких знаходиться із цим елементом у відношенні еквівалентності, тобто
K (m) = {mi / mi ~ m}.
Розбивкою множини М називається сімейство непустих попарно непересічних підмножин (класів), об'єднання яких збігається з М.
Проілюструємо процедуру побудови розбивки множин.
Нехай на множині М задане відношення еквівалентності R . Здійснимо наступну побудову:
- виберемо елемент т1 і утворимо підмножину (клас еквівалентності), що складається з елемента т1 і всіх елементів, еквівалентних т1 : K (т1) ;
і утворимо підмножину (клас еквівалентності), що складається з елемента т1 і всіх елементів, еквівалентних т1 : K (т1) ;
- виберемо елемент 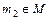 ,
,  і утворимо підмножину (клас еквівалентності) елемента т2 : K (т2) , що складається з елемента т2 і всіх елементів, еквівалентних йому , і т.д. У результаті такої побудови вийде система класів еквівалентності K (т1), K (т2), … (можливо нескінченна) така, що будь-який елемент із множини М входить хоча б в один клас, тобто
і утворимо підмножину (клас еквівалентності) елемента т2 : K (т2) , що складається з елемента т2 і всіх елементів, еквівалентних йому , і т.д. У результаті такої побудови вийде система класів еквівалентності K (т1), K (т2), … (можливо нескінченна) така, що будь-який елемент із множини М входить хоча б в один клас, тобто 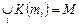 .
.
Дана система має наступні властивості:
1. класи еквівалентності попарно не перетинаються: 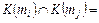 Ø;
Ø;
2. будь-які два елементи з одного класу еквівалентні;
 3. будь-які два елементи з різних класів нееквівалентні.
3. будь-які два елементи з різних класів нееквівалентні.
Побудована розбивка (система класів) називається системою класів еквівалентності по відношенню R .
Якщо бінарне відношення є бінарним відношенням еквівалентності, то його матрицю суміжності можна привести за допомогою перестановок рядків (стовпців) до виду
Тут біля головної діагоналі розташовані підматриці, що складаються з одиниць, інші елементи матриці дорівнюють нулю. Кожна підматриця відповідає класу еквівалентності.
§ 6. БІНАРНЕ ВІДНОШЕННЯ ПОРЯДКУ. УПОРЯДКОВАНІ МНОЖИНИ
Читайте також:
- I визначення впливу окремих факторів
- II. Багатофакторний дискримінантний аналіз.
- Абіотичні та біотичні фактори.
- Агрегування та факторизація
- Адаптація до абіотичних факторів середовища.
- Адаптація організму до зовнішніх факторів середовища.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Анализ влияния факторов на изменения фонда рабочего времени
- Аналіз впливу факторів на зміну сумми гуртової реалізації
- Аналіз факторів впливу на обсяги виробництва суспільного продукту.
- Аналіз факторів і причин відхилень від плану введення виробничих потужностей і основних фондів
- Аналіз факторів, що впливають на цінову політику.
| <== попередня сторінка | | | наступна сторінка ==> |
| Способи задання бінарних відношень | | | Бінарне відношення порядку. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |