• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вибір кращих альтернатив за допомогою бінарних відношень

Основне завдання децидента в процесі прийняття рішення – виділити одну чи кілька найкращих альтернатив. Якщо наше завдання – отримати максимальний дохід, то найкращій альтернативі відповідає поняття максимуму за певним відношенням переваги Р чи побудова множини «найкращих», але непорівняльних між собою альтернатив.

Тоді найдоцільніше використати поняття мажоранти; у разі ж, наприклад, мінімізації збитків, більше підходять поняття мінімуму та міноранти.

Інтуїтивно зрозуміло, що між цими поняттями мають існувати певні взаємні зв’язки. Це справді так, і ці зв’язки відображають наступні твердження.

Позначимо множину максимумів множини А за відношенням Р як A⁺(Р), мажорант – A₊(Р), мінімумів – А^–(Р), мінорант – А_–(Р):

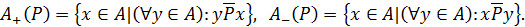
Між ними існують залежності, сформульовані в таких твердженнях.

ТВЕРДЖЕННЯ 2.23. Для максимумів, мінімумів, мажорант і мінорант множини A за відношенням Р виконуються співвідношення

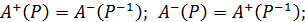
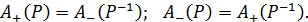
Доведення. Нехай 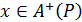, тобто для всіх уÎА виконується співвідношення хРу, або уР^–1х. За означенням мінімуму 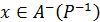, тобто 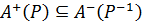. Нехай тепер 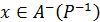. Це означає, що для всіх уÎА виконується співвідношення уР^–1х, або хРу, тобто 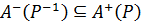. Зіставивши отримані включення, одержимо . Інші співвідношення доводяться аналогічно.¨

ТВЕРДЖЕННЯ 2.24. Для максимумів, мінімумів, мажорант і мінорант множини A за відношенням Р виконуються співвідношення 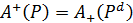, , 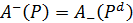де Р^d – двоїсте до Р відношення.

Доведення. Нехай 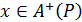, тобто для всіх уÎА виконується співвідношення хРу, або уР^–1х, тому не виконується yP^dx. За означенням мажоранти 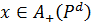, тобто 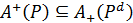. Нехай тепер 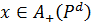. Це означає, що для всіх уÎА виконується співвідношення yP^dx. Оскільки (P^d)^d = Р, то для всіх уÎА виконується хРу, і за означенням максимуму 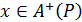, тобто 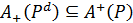. Зіставивши отримані включення, одержимо .

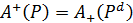Аналогічно доводиться співвідношення .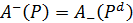

Приклад 2.36. Відношення Р задано матрицею. Його граф подано на рис. 2.15.

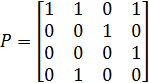
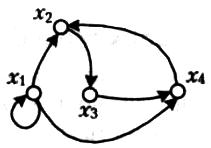Рис. 2.15. Граф відношення P

Відношення Р не має максимумів, мажорант, мінімумів і мінорант.

Розглянемо відношення R. Його граф подано на рис. 2.16.

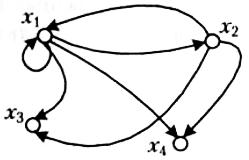Рис. 2.16. Граф відношення R

x₁ – максимум, x₃, x₄ – міноранти. Мажорант та мінімумів відношення R не має.

Відношення Q задано матрицею. Його граф подано на рис. 2.17.

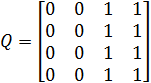
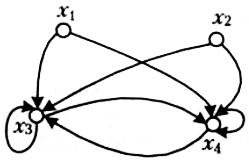Рис. 2.17. Граф відношення Q

x₁, x₂ – мажоранти, x₃, x₄ – мінімуми. Мінорант і максимумів відношення Q не має.

Читайте також:

1. Алгоритм планування податкових платежів. Вибір оптимального варіанту оподаткування та сплати податків.
2. Альтернативи діалектики
3. Альтернативи діалектики. Метафізика, софістика, еклектика, догматизм, релятивізм.
4. Альтернативи діалектики. Метафізика, софістика, еклектика, догматизм, релятивізм.
5. Альтернативна вартість і незворотні витрати
6. Альтернативна вартість та її використання у проектному аналізі
7. Альтернативна реалізація із вільним вихідним кодом – сервер SAMBA
8. Альтернативні варіанти геополітичної орієнтації України
9. Альтернативні варіанти довгострокового фінансування діяльності підприємства
10. Альтернативні джерела формування підприємницького капіталу
11. Альтернативні можливості виробництва масла і тракторів
12. Альтернативні можливості виробництва масла та гармат.

Переглядів: 1672