Функція вибору

Подання переваг децидента

Функції та механізми вибору

Залежно від характеру системи переваг децидента змінюються й альтернативи, обрані з пред’явлених для вибору в певній ситуації. Це зумовлено тим, що в одній і тій самій ситуації уявлення різних осіб про кращі альтернативи можуть суттєво різнитися. При цьому дециденти зазвичай раціонально обґрунтовують вибір. Отже, бінарне відношення порівняльності Р, побудоване для конкретної ситуації, чинне лише для конкретного децидента й лише для цієї ситуації. Це означає, що за відомим вибором у конкретній ситуації неможливо дійти певних висновків щодо причин, що спонукали вибрати саме ці альтернативи, а не інші.

Щоб вийти з цього положення, доцільно розглядати множину можливих альтернатив у, подібних ситуаціях прийняття рішень, і формалізувати поняття вибору для них. У конкретній ситуації розглядають певну підмножину X множини можливих альтернатив А (X Í А), і вибирають з альтернатив, що належать цій множині X. Для формалізації вибору у взаємозалежних (через множину можливих альтернатив А) ситуаціях використовують поняття функції вибору.

ОЗНАЧЕННЯ 2.45. Функцією вибору С називається відображення, яке кожній X Í А ставить у відповідність підмножину Y Í X альтернатив, котрі обирає децидент:

С: X ® Y, або Y = С(Х), С(Х) Í X.

Функція вибору має задовольняти умову

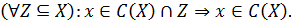
Ця умова відповідає вибору «серед кращих» альтернатив. Інакше кажучи, вибір в конкретній ситуації кращих альтернатив із підмножини Z множини X, для якої задано функцію вибору, дасть у результаті підмножину кращих у множині X альтернатив 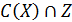, які водночас належать підмножині Z (рис. 2.18). Якщо C(Z) = Æ, то формально можна вважати, що виникає ситуація відмови від вибору.

Функцію вибору можна поставити у відповідність кожному бінарному відношенню R із носієм А. Нехай для вибору пред’явлено довільну підмножину X Í А. Відношення R звужується на множину X і функцію вибору можна визначити двома способами. З одного боку, це всі елементи x Î X, з якими не перебуває у відношенні R жоден елемент у Î X, тобто мажоранти множини X за звуженням відношення R на X. З іншого боку, це ті елементи x Î X, для яких xRy для всіх у Î X, тобто максимуми множини X за звуженням відношення R на X.

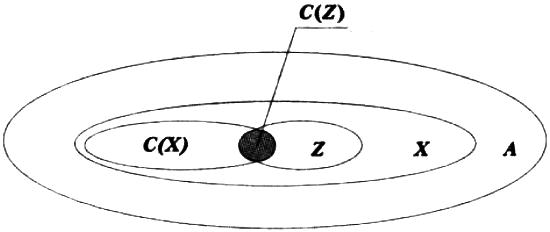
Рис. 2.18. Графічне подання вибору

Отже, на множині А існують дві функції вибору:

Якщо R_X – звуження відношення R на X Í А, то

Множина складається з мажорант 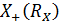, а множина 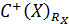– з максимумів .

Функції вибору С₊(Х) і С⁺(Х) пов’язані між собою, про що свідчить таке твердження.

ТВЕРДЖЕННЯ 2.25. Для функцій вибору і виконуються співвідношення

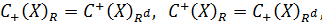
де R^d – відношення, двоїсте до R.

Справедливість цього твердження випливає з того, що

, та .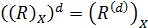

Тому зазвичай розглядають одну функцію вибору і вважають, що її породжує відношення R. Зауважимо, що таке бінарне відношення існує не для будь–якої функції вибору. Функції вибору, породжені бінарними відношеннями, називаються нормальними.

Уважатимемо, що множина–носій бінарного відношення А являє собою універсальну множину альтернатив, тобто А містить у собі всі альтернативи, можливі в певній задачі вибору за різних умов. Множину X Í А альтернатив, пред’явлених для вибору в певній ситуації, будемо називати пред’явленням. За цих умов результат вибору задано функцією вибору Y = С(Х), С(Х) Í X.

Отже, довільну функцію С: 2^A ® 2^A (2^A – множина всіх підмножин множини А), таку, що С(Х) Í X для всіх X Î 2^A, можна розглядати як функцію вибору. Альтернативу х Î А називатимемо прийнятною для С, якщо існує пред’явлення X, у якому її обирають, тобто 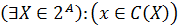. Окрім того, нехай найчастіше виконується умова вибору прийнятних альтернатив – якщо пред’явлення складається з однієї альтернативи, то її обирають, тобто

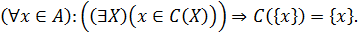
Апарат функцій вибору зручний для формулювання змістовних властивостей, за виконання яких вибір можна вважати «розумним», «несуперечливим», «раціональним», а також дослідження та формалізації різноманітних механізмів і принципів вибору [25].

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Вибір кращих альтернатив за допомогою бінарних відношень	\|	Неповні функції вибору

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.017 сек.