• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Види механізмів вибору

Клас усіх функцій вибору R Î Q позначатимемо надалі як X. Розглянемо важливі на практиці механізми вибору, реалізовані декількома наявними бінарними відношеннями, які належать до множини Р, Р = {Р₁, ..., Р_n). Для визначеності правила вибору R будемо вважати, що його можна реалізувати, знайшовши мажоранти А₊(Q\Е) певного антирефлексивного відношення Q\E, (де Q – довільне задане відношення, Е – діагональне відношення) чи максимуми 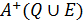відношення 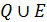, зведеного до рефлексивного вигляду. Є такі основні механізми вибору за декількома відношеннями: вибір за агрегованим відношенням, паралельний вибір, послідовний, узагальнений покроковий.

Вибір за агрегованим відношенням виконують, задавши (побудувавши, синтезувавши) функції F: Р Þ Q, яка множині Р = {Р₁, ..., Р_n} заданих відношень ставить у відповідність деяке відношення Q = F{Р₁, ..., Р_n}, що називається агрегованим. Остаточно альтернативи вибирають за правилом L, якому відповідає функція вибору .

Послідовний вибір провадять упорядкуванням відношень, що є елементами множини Р, з подальшим послідовним вибором в n етапів. На і–му етапі вибирають з альтернатив, що є результатом вибору за допомогою послідовного застосування на попередніх етапах пар , де Р_k, L_k –відношення та конкретне правило, за яким виконується вибір на k–му кроці. Якщо вибір на i–му кроці реалізовано за допомогою функції вибору , а пред’явлення – це множина (X, X Í В, В Í 2^A), то функція послідовного вибору С_– має вигляд

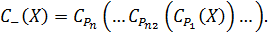
Паралельний вибір за відношеннями {Р₁, ..., Р_n} виконується за допомогою незалежного вибору з пред’явлення X за кожним із цих відношень і відповідним правилом вибору L_i з множини L = {L₁, ..., L_n}, що реалізується множиною функцій вибору . Далі, виходячи з цього сукупного вибору, за допомогою композиції F C_P Þ C (зазвичай для цього застосовують операції над множинами) роблять остаточний вибір

Щоб правило композиції могло бути реалізоване у вигляді функції вибору, функція композиції F має задовільняти умову F(0, 0, ..., 0) = Æ (тобто вибір із порожньої множини має бути порожньою множиною) й умову монотонності (тобто або F = Æ, або цю функцію можна було описати через операції та ).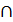

Узагальнений покроковий вибір будують, комбінуючи на різних кроках вищенаведені механізми. Розглянемо достатньо загальний механізм вибору , структуру якого задано антирефлексивним бінарним відношенням Р (якщо є довільне бінарне відношення Q, то воно зводиться до антирефлексивного Р = Q\E, де Е – діагональне відношення) та конкретним правилом вибору мажорант відношення Р з носієм А.

Побудуємо логічну функцію вибору, що відповідає цьому механізму. Альтернативу x_i Î А обирають у пред’явленні тоді, коли b_i(Х) = 1 (b_i(Х) = 1, якщо x_i Î X, і (b_i(Х) = 0, якщо x_i Ï X і в пред’явленні X немає жодної такої альтернативи х_j, що х_jP^–1, тобто , , 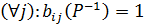і логічна форма функції вибору має вигляд

.

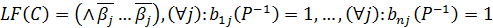Приклад 2.37. Побудуємо логічну форму функції вибору для механізму вибору , якщо задано бінарне відношення

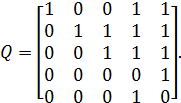
Побудуємо відповідне антирефлексивне відношення Р й обернене P^–1

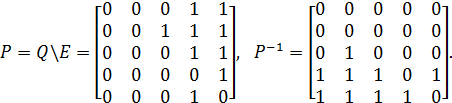
Логічна форма функції вибору буде така: .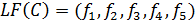

За допомогою вищенаведених формул отримаємо

Нехай b(Х) = (1, 0, 1, 1, 1), тобто пред’явлення має вигляд X = (х₁, х₃, х₄, x₅), а тому в результаті вибору

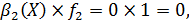
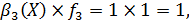
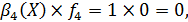
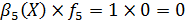
та С(Х) = С({х₁, х₃, х₄, x₅}) = {х₁, х₃}.

Розглянемо механізм вибору , структуру якого задано рефлексивним бінарним відношенням Р (довільне бінарне відношення Q зводиться до рефлексивного за співвідношенням , де Е – діагональне відношення) та конкретним правилом вибору максимумів відношення Р з носієм А. Логічну форму функції вибору для цього механізму можна побудувати, виходячи з того, що альтернативу х_i Î А вибирають у пред’явленні X (X Í В, В Í 2^A) тоді й лише тоді, коли b_i(Х) = 1, і в пред’явленні для всіх х_j Î X справедливе твердження х_iPх_j, тобто . Логічна_форма відповідної функції вибору така:

.

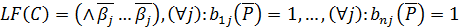Читайте також:

1. E) теорія раціонального вибору.
2. Альтернативність ресурсів і проблема економічного вибору
3. Аспекти вибору системи складування
4. Варіанти вибору ділової їжі (буфет або a la carte).
5. Варіанти вибору ринкових сегментів
6. Вибір будівельних машин, механізмів і технологічного транспорту для комплексної механізації монтажних робіт
7. Види механізмів здійснення міжбанківських переказів
8. Види та критерії вибору заходів медичного характеру
9. Визначення коректних варіантів вибору
10. Вимоги безпеки при експлуатації машин та механізмів.
11. ВИМОГИ ЩОДО ЕКСПЛУАТАЦІЇ МАШИН І МЕХАНІЗМІВ

Переглядів: 1771