• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні задачі дослідження та застосування механізмів вибору

У ході дослідження та застосування механізмів вибору виникають задачі аналізу, синтезу й апроксимації процедур вибору реальних децидентів, а також оцінювання складності реалізації механізму виборів та їх оптимізації.

Розв’язком задачі аналізу є функція вибору C_R, що реалізує механізм 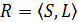. Якщо множина можливих альтернатив А скінченна, то розв’язати цю задачу не важко. Найпростіший метод полягає в тому, що для кожного пред’явлення X за заданою структурою S і конкретним правилом вибору L механізму вибору R визначають множину вибраних альтернатив із подальшим відтворенням за цією інформацією таблиці можливих пред’явлень X = 2^A та побудовою функції вибору C_R. Однак кількість рядків такої таблиці, які описують функцію вибору, дорівнює 2ⁿ, де n – кількість альтернатив, тобто таблиця зростає експоненційно зі зростанням розмірності n = саrd(A) задачі, хоча обсяг інформації, що описує змістовні механізми вибору, зазвичай обмежено поліномом від кількості n можливих альтернатив.

Отже, методи аналізу механізмів вибору, у яких функцію вибору подано таблицею, неефективні, однак табличне подання доцільне, коли потрібно описати результати експериментального вибору, тому що в цьому разі розмір таблиці порівнянний з обсягом спостережень. Апарат алгебри Буля, використовуваний для описання функцій вибору – об’єднувальна основа для побудови та дослідження різноманітних моделей вибору. Часто він дає змогу компактно описати теоретичні результати. Крім того, аналіз потрібен також для дослідження якісних властивостей функцій вибору, реалізовуваних механізмами певного заданого класу, і виявлення деяких кількісних параметрів функції вибору C_R.

Задача синтезу одна з найважливіших у побудові моделі вибору. Вона полягає в синтезі за функцією вибору (зазвичай, неповною) механізму вибору певного класу, що її реалізує. Оскільки функція вибору найчастіше часткова та ґрунтується на експериментальних даних, а механізм вибору має бути придатний у довільних ситуаціях, то він має задовільно прогнозувати вибір і в тих ситуаціях, яких не було в експерименті. Як показує досвід, це краще роблять моделі механізмів вибору з невеликою складністю. У процесі синтезу потрібно вміти використовувати додаткову інформацію, яку можна отримати від децидента, а також певні напівформальні вимоги (рівновага, справедливість, компромісність). Задача синтезу належить до NР–повних, і в загальному вигляді її не можна розв’язати за допомогою ефективних алгоритмів. Якщо клас механізмів вибору повний, то виконується умова

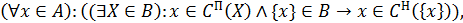
тобто існує довизначення функції С неповного вибору

що задовільняє умову

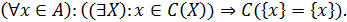
Задача синтезу функції вибору в цьому класі механізмів вибору Q₀ завжди має розв’язок.

Якщо функцію вибору С не можна реалізувати механізмами вибору заданого вигляду, то виникає задача її апроксимації, тобто пошуку в певному розумінні найкращого наближення до неї. Коли вводити певну метрику недоцільно чи це неможливо достатньо обґрунтувати, розглядають якісь абсолютні верхнє та нижнє найкращі наближення – верхню та нижню апроксимації. їх задають через мажоранти й міноранти функцій неповного вибору.

ОЗНАЧЕННЯ 2.48. Мажорантою С₊ функції неповного вибору (С^П, С^Н, В) називається всюди визначена функція, для якої виконується умова

де X – пред’явлення, В Í 2^A – множина можливих пред’явлень, (С^П(Х), С^Н(Х)) – множини вибраних і відкинутих альтернатив відповідно.

ОЗНАЧЕННЯ 2.49. Мінорантою С_– функції неповного вибору (С^П, С^Н, В) називається всюди визначена функція, для якої виконується умова

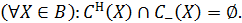
ОЗНАЧЕННЯ 2.50. Функція С_B Î X⁰ називається верхньою апроксимацією функції С в класі механізмів Q (де X⁰ – множина всюди визначених функцій, які реалізуються в М), якщо виконується умова

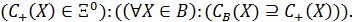
Аналогічно функція С_H Î X⁰ називається нижньою апроксимацією функції С в класі механізмів Q, якщо виконується умова

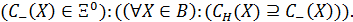
Постановки задач про верхню та нижню апроксимацію природньо виникають тоді, коли вибір С – проміжний етап, за результатами якого буде виконано остаточний вибір. На цьому етапі використовують вибір С, породжений механізмом із певного класу X. Якщо ми хочемо розглянути всі альтернативи, вибрані за допомогою функції С, то потрібно знайти верхню апроксимацію. Коли ж висуното вимогу, щоб жодну з відкинутих за допомогою функціїї С альтернатив не було остаточно вибрано, – шукають нижню апроксимацію.

Аналогічні задачі апроксимації можна ставити й розв’язувати не лише для функцій, а й для механізмів вибору. Велике значення в дослідженні механізмів вибору мають характеристики їх складності. їх знаходження зазвичай зводиться до отримання асимптотичних оцінок для певних суттєвих параметрів механізмів вибору. Ці оцінки отримуються конструктивно, що дозволяє використати їх при розробці та оптимізації конкретних процедур, а також прогнозувати орієнтовну складність реалізації того чи іншого механізму вибору. Задача синтезу може мати багато розв’язків, тому що одній і тій самій функції вибору можуть відповідати багато механізмів, що її реалізують.

Для досягнення певної однозначності до синтезованого механізму пред’являють додаткові вимоги, що стосуються складності. Найпростішими мірами складності можуть бути такі:

v для вибору на грунті відношення – кількість пар, що його складають;

v для механізму послідовного вибору – кількість відношень (глибина вибору);

v для багатокрокових схем – кількість кроків.

Серед проблем оптимізації найважливішою є проблема оптимального синтезу й оптимізації механізмів вибору. Мета оптимального синтезу – побудова механізму вибору з мінімальною складністю. Для більшості випадків не знайдено ефективних рішень, а для деяких задач доведено їх NP–повноту. Тому вимоги до методів синтезу ослаблюють, і найчастіше ставлять задачу розробки методів синтезу, що забезпечують гарантовану оцінку складності реалізації функції із заданими параметрами.

До оптимального синтезу близька задача оптимізації механізмів, що ґрунтується на понятті еквівалентних механізмів вибору. Будемо вважати механізми М₁, М₂, ..., М_k еквівалентними, якщо . Механізм вибору називають мінімальним у класі X, якщо він має мінімальну складність серед усіх еквівалентних до нього механізмів із Q. Задача оптимізації на класі механізмів Q полягає в тому, щоб за заданим конкретним механізмом М Î Q побудувати еквівалентний до нього мінімальний механізм, який належить М. Ця задача теж належить до класу NP–повних, а тому на практиці доцільно застосовувати еквівалентні перетворення механізмів вибору, що дають змоіу спростити її.

Отже, у ході дослідження та застосування механізмів і функцій вибору доводиться розв’язувати такі основні задачі:

v аналізу;

v синтезу;

v апроксимації реального вибору децидента;

v оцінювання складності реалізації механізмів вибору;

v оптимізації механізмів вибору.

Читайте також:

1. E) теорія раціонального вибору.
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. V. Виконання вправ на застосування узагальнювальних правил.
4. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
5. Автомобільні ваги із застосуванням цифрових датчиків
6. Адаптовані й специфічні методи дослідження у журналістикознавстві
7. Адвокатура в Україні: основні завдання і функції
8. Акти застосування норм права в механізмі правового регулювання.
9. Акти застосування юридичних норм: поняття, ознаки, види.
10. Акти правозастосування, їх види
11. Акти правозастосування.
12. Актуальність дослідження

Переглядів: 864