Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Відношення домінування та байдужості

Вивчаючи відношення переваги між реальними об’єктами, можна виокремити в ньому два аспекти: один відображає перевагу (переважання, домінування) одного об’єкта над іншим, а другий – байдужість (індиферентність, толерантність) об’єктів. Тому означають два відношення між об’єктами, які надалі називатимемо відношеннями домінування та байдужості. Наведемо кілька прикладів.

Приклад 2.31. Турнір, де результат зустрічі двох учасників – виграш одного з них або нічия (як у шахах). На множині учасників турніру задають відношення домінування та байдужості: а домінує b означає, що а виграв у b; а та b байдужі означає, що вони зіграли внічию.

Приклад 2.32. Голосування, проведене для групи кандидатів. На множині кандидатів а домінує b, якщо за нього подано більше голосів, ніж за b; а та b байдужі, якщо за них подано однакову кількість голосів (це стосується лише двох кандидитів; інші можливі випадки ми розглянемо в моделях прийняття рішень шляхом голосування).

Приклад 2.33. Відношення переваги за віком. Для двох осіб уважаємо, що а домінує b, якщо а старший за b; а та b байдужі, якщо вони одного віку. У психологічному аналізі прийнятнішими є такі означення відношень домінування та байдужості людей за віком, коли домінування означає істотну перевагу, а байдужість – близькість віку. Наприклад, для двох осіб а та b вважаємо, що а домінує b, якщо він старший за b не менш ніж на 5 років; а та b байдужі, коли різниця їх віку не перевищує 2 років.

Приклад 2.34. Відношення підпорядкування всередині організації. Для двох членів організації один домінує іншого, якщо він керує ним.

За всієї різноманітності ситуацій, у яких розглядають відношення домінування та байдужості, ці відношення мають спільні властивості. Позначимо як a відношення домінування ((а,b)Îa означає, що а домінує b), b – відношення байдужості ((а,b)Îb означає, що а та b байдужі). Ця структура має такі властивості.

v Відношення домінування a асиметричне: не може бути такого, щоб, скажімо, на тенісному турнірі учасник а переміг учасника b й b переміг а; щоб кандидат а зібрав більше голосів, ніж кандидат b, а b – більше, ніж а (в одному й тому самому турі голосування), і т.ін. Отже, .

v Відношення байдужості b симетричне: наприклад, якщо учасник а зіграв унічию з учасником b, то й b зіграв унічию з а; якщо вік особи а близький до віку особи b , то й вік b близький до віку а, тобто .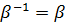

v Жодна пара об’єктів не належить водночас до відношень домінування та байдужості, тобто .

v Уважатимемо, що кожен об’єкт байдужий до самого себе (тобто відношення b рефлексивне). Ця умова має швидше характер угоди, тому що в ситуаціях, аналогічних до наведених вище прикладів, об’єкт не порівнюють із самим собою. Однак вона цілком відповідає змісту, який зазвичай вкладають у поняття байдужості.

Наведеними умовами вичерпуються всі загальні властивості відношень такого типу. Зафіксуємо це в такому формальному означенні.

ОЗНАЧЕННЯ 2.44. Пара відношень (a,b) з множиною носієм А задає на цій множині структуру «домінування–байдужість», де a – відношення домінування, b – байдужості, якщо відношення a асиметричне, b – симетричне та рефлексивне (тобто є відношенням толерантності), а .

Легко перевірити, що коли (a,b) – структура «домінування–байдужість» на множині А, то пара відношень (a^–¹,b) також утворює структуру «домінування–байдужість» на А. У цьому разі a^–¹ називають відношенням домінованості.

Важливими є структури, у яких або будь–які два об’єкти з досліджуваної множини байдужі, або один із них домінує іншого (як у наведених вище прикладах); таку структуру «домінування–байдужість» називатимемо лінійною. Наприклад, структура «домінування–байдужість» лінійна, якщо турнір проводять за коловою системою (кожен грає з кожним). Зручно подати властивість лінійності структури «домінування–байдужість», означивши поняття порівняльності об’єктів. Уважатимемо об’єкти а та b порівняльними, якщо вони байдужі чи один із них домінує іншого, в іншому випадку об’єкти а та b вважають непорівняльними.

Множина пар порівняльних об’єктів утворює відношення порівняльності, а множина пар непорівняльних об’єктів – відношення непорівняльності. Структура «домінування–байдужість» на множині А лінійна тоді й лише тоді, коли будь–яка пара об’єктів порівняльна, тобто коли відношенням порівняльності є А×А.

Для будь–яких двох елементів а та b, довільно взятих із множини, на якій задано структуру «домінування–байдужість», обов’язково виконується точно одна з таких чотирьох умов:

v а домінує b;

v b домінує а;

v а та b байдужі;

v а та b непорівняльні.

У разі лінійної структури обов’язково виконується одна з перших трьох умов.

Структуру «домінування–байдужість» подається за допомогою матриці таким чином; у клітинці, що відповідає рядку елемента а та стовпцю елемента b, ставимо 1, якщо а домінує b; 0, якщо b домінує а; 1/2, якщо а та b байдужі. Тобто, матрицю «домінування–байдужість» будують за тим самим принципом, що й таблиці спортивних турнірів. Структура «домінування–байдужість» лінійна тоді й лише тоді, коли в цій матриці немає порожніх клітинок.

Таке подання є надлишковим (хоча й наочним), тому що структуру «домінування–байдужість» можна задати за допомогою одного відношення. Нехай (a,b) – структура «домінування–байдужість» на множині А. Припустімо, що 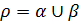. Знайдемо симетричну і асиметричну частину 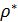відношення .

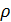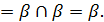
Тут використано те, що .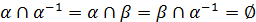

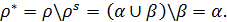
В останньому переході потрібно взяти до уваги, що . У цьому (і лише в цьому) разі операції об’єднання та різниці множин нейтралізують одна одну. Виявилося, що початкові відношення a й b можна «відновити», якщо відоме їх об’єднання: a – асиметрична, а b – симетрична частина відношення . Отже, довільну структуру «домінування–байдужість» можна означити за допомогою одного бінарного відношення – об’єднання відношень домінування та байдужості. Називатимемо його відношенням переваги.

Які ж властивості має відношення переваги? Інакше кажучи, якщо 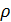– довільне відношення на множині А, то які необхідні та достатні умови того, щоб для структури «домінування – байдужість» (a,b) з носієм А справджувалася рівність 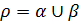? Звичайно, відношення 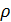має бути рефлексивним (тому що відношення b рефлексивне). Виявляється, що на відношення 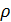не потрібно накладати жодних інших умов, тобто довільне рефлексивне відношення 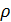може бути відношенням переваги для структури «домінування – байдужість».

Справді, нехай 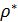– асиметрична, а – симетрична складова рефлексивного відношення 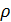. Тоді відношення 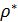асиметричне, – симетричне та рефлексивне, і 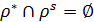, тому пара відношень 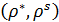утворює на множині А структуру «домінування–байдужість»; відповідне їй відношення переваги – початкове відношення .

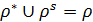Отже, будь–яке відношення може бути відношенням переваги. Потрібно лише перетворити його на рефлексивне, додавши петлі, і взяти як відношення домінування асиметричну складову, а як відношення байдужості – симетричну складову отриманого відношення. При цьому його лінійність рівносильна лінійності відповідної структури «домінування –байдужість».

Транзитивність структури «домінування – байдужість»

Відношення домінування та байдужості, узагалі кажучи, можуть бути нетранзитивними. Тому доцільно виділити такі структури «домінування–байдужість», у яких ці відношення транзитивні (тобто якщо елемент а домінує елемент b, а b домінує с, то а домінує с; якщо елемент а байдужий елементу b, а b байдужий с, то а байдужий с. Сформулюємо ще одну вимогу: для довільної пари об’єктів, що належить відношенню домінування, заміна одного з об’єктів байдужим до нього зберігає домінування, тобто

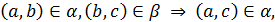
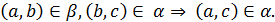
Ці умови відображають транзитивність відношення a стосовно відношення b. Називатимемо структуру «домінування–байдужість» транзитивною, якщо відношення домінування та байдужості транзитивні та відношення домінування транзитивне стосовно відношення байдужості.

З’ясуємо, яку роль відіграє відношення переваги для транзитивних структур «домінування–байдужість». Якщо відношення a й b транзитивні та відношення a транзитивне відносно b, то – транзитивне відношення. Окрім того, відношення рефлексивне як довільне відношення переваги, тому це відношення квазіпорядку. Навпаки, нехай 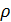– довільне відношення квазіпорядку на множині А. Його асиметрична частина 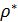та симетрична частина транзитивні і відношення 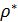транзитивне щодо . Отже, структура «домінування–байдужість» 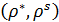, що відповідає відношенню 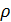, транзитивна. Доходимо висновку, що 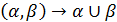є взаємно–однозначною відповідністю між транзитивними структурами «домінування–байдужість» на множині А та відношеннями квазіпорядку на цій множині; задання транзитивної структури «домінування – байдужість» рівносильне заданню лише відношення квазіпорядку. Якщо, крім цього, відношення байдужості тотожне (тобто кожен об’єкт байдужий лише сам до себе), то відповідне відношення квазіпорядку являє собою відношення порядку.

Система переваг децидента – це сукупність формальних і неформальних, статичних і динамічних правил та умов, які дають йому змогу вибрати одну чи кілька альтернатив у певній ситуації прийняття рішень. Отже, система переваг має як статичну складову, що залишається постійною незалежно від умов зовнішнього середовища та відображає сталі, глибинні, у певному розумінні об’єктивні правила, за допомогою яких можна відкинути неперспективні альтернативи, так і динамічну, яка відзеркалює змінність переваг залежно від умов зовнішнього середовища, внутрішню суперечливість і нечіткість уявлень децидента про кращі альтернативи, його суб’єктивність.

При порівнянні альтернатив можуть виникнути ситуації двох типів:

v децидент вирішив, що альтернатива х_i переважає (домінує чи краща за неї) альтернативу х_j,

v децидент не може розрізнити за якістю альтернативи х_i та x_j (альтернативи рівнозначні, подібні, байдужі).

Отже, статичну складову системи переваг децидента можна моделювати за допомогою структури «домінування –байдужість».

Приклад 2.35. Нехай задано рефлексивне відношення P:

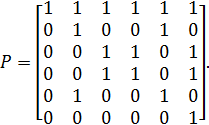
Побудуємо відповідні йому відношення байдужості Р^Е та домінування Р^D:

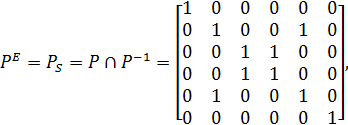
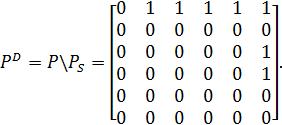
Знайдемо відношення непорівняльності:

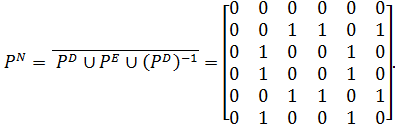
Оскільки P^N ¹ Æ, то відношення Р не є лінійним. Крім того, оскільки відношення Р транзитивне (що можна перевірити, побудувавши транзитивне замикання), то Р – квазіпорядок.

Отже, якщо носій бінарного відношення А = {х₁, х₂, …, х_n} – множина альтернатив, для децидента, то відношення Р рефлексивне, тому є відношенням порівняльності, a P^N – відношенням непорівняльності. Найчастіше відношення порівняльності постулюють як транзитивне. Якщо ж отримане за допомогою експертного опитування відношення виявляється нетранзитивним, то намагаються зробити його транзитивним, додатково опитуючи децидента й корегуючи відношення.

Оскільки відношення Р в цьому разі транзитивне та рефлексивне, то воно є квазіпорядком. Коли ще й P^N ¹ Æ, то цей квазіпорядок лінійний, тому можна однозначно обрати одну чи кілька рівноцінних найкращих альтернатив (зазвичай це малоймовірно). Якщо відношення порівняльності має властивості рефлексивності, транзитивності й антисиметричності, то воно є відношенням порядку.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Упорядковані множини в прийнятті рішень	\|	Вибір кращих альтернатив за допомогою бінарних відношень

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.