• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Упорядковані множини в прийнятті рішень

Подання системи переваг бінарними відношеннями

Основні результати теорії впорядкованих множин дають змогу обґрунтувати процедури перетворення та модифікації системи переваг децидента. Аксіома вибору – одна з найцікавіших аксіом теорії множин, безпосередньо пов’язана з прийняттям рішень [43]. В найпростішому формулюванні ця аксіома стверджує наступне.

Аксіома вибору. Якщо X – об’єднання непорожніх множин Х_i, що не перетинаються, то існує щонайменше одна підмножина 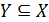, перетини якої з кожною множиною Х_i одноелементні.

У популярних виданнях час від часу стверджують, що аксіома вибору чимось відрізняється за своїм статусом від інших аксіом теорії множин, хоча ще в 1938 – 1940 р. Курт Ґедель довів, що за умови несуперечливості аксіоматичної теорії множин включення цієї аксіоми не веде до суперечливості цієї теорії. У формулюванні, запропонованому Ернестом Цермело, не потрібно, щоб підмножини X_i не перетиналися.

Аксіома вибору Цермело. Для кожної множини X непорожніх множин X_i, іÎІ, існує така функція

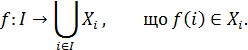
Розглянемо важливі для прийняття рішень поняття максимуму та мінімуму, а також мажоранти і міноранти за певним відношенням R.

ОЗНАЧЕННЯ 2.39. Елемент хÎА, де А – множина–носій відношення R, називається його максимумом, якщо 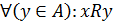, тобто xRy для всіх елементів множини–носія А.

ОЗНАЧЕННЯ 2.40. Елемент хÎА, де А – множина–носій відношення R, називається його мінімумом, якщо 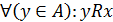, тобто yRx для всіх елементів множини–носія А.

Максимумів і мінімумів за певним відношенням може й не бути. Так, множина всіх дійсних чисел не має ні мінімуму, ані максимуму за відношенням «³». Водночас множина всіх невід’ємних чисел за цим самим відношенням має мінімум – 0, але не має максимуму.

Від максимуму та мінімуму слід відрізняти поняття мажоранти і міноранти.

ОЗНАЧЕННЯ 2.41. Елемент хÎА, де А – множина–носій відношення R, називається його мажорантою, якщо , де 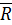– доповнення до відношення R, тобто для всіх елементів множини–носія А.

ОЗНАЧЕННЯ 2.42. Елемент хÎА, де А – множина–носій відношення R, називається його мінорантою, якщо 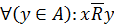, тобто 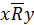для всіх елементів множини–носія А.

Приклад 2.27. Розглянемо відношення R, задане таким графом із двома компонентами зв’язності (рис. 2.10).

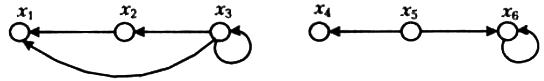
Рис. 2.10. Граф незв’язного бінарного відношення

Для цього бінарного відношення х₁, х₄ – міноранти, х₅ – мажоранта; мінімумів та максимумів немає.

ОЗНАЧЕННЯ 2.43. Множина А називається впорядкованою за відношенням строгого порядку D (транзитивним і асиметричним), якщо вона є носієм цього відношення .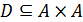

Надалі впорядковану множину будемо позначати двійкою 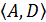. Елемент уÎА називається мажорантою підмножини 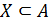, якщо він є мажорантою звуження відношення D на підмножині X. Впорядкована множина називається індуктивною, якщо кожна підмножина X, яка є ланцюгом, має мажоранту.

Індуктивні впорядковані множини мають одну важливу властивість, що формулюється лемою Куратовського – Цорна.

Лема Куратовського – Цорна. В індуктивній упорядкованій множині для кожного елемента існує мажоранта.

Розглянемо властивості впорядкованих множин, що безпосередньо застосовуються в задачах прийняття рішень. Нехай D – відношення строгого порядку з носієм А. Бінарне відношення Р з носієм А називається сумісним зі строгим порядком D, якщо граф відношення 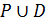––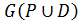 не має контурів і петель.

ТВЕРДЖЕННЯ 2.20. Бінарне відношення Р сумісне зі строгим порядком D, якщо відношення 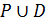міститься в якомусь відношенні строгого порядку з носієм А.

Доведення. Нехай 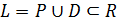, де R — відношення строгого порядку. Тоді граф 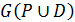не має контурів і петель, бо інакше контур або петля графа 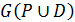були б також контуром або петлею графа G(R), а граф відношення строгого порядку не має контурів. Навпаки, якщо граф 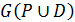не має петель і контурів, то його відношення досяжності L асиметричне, тобто граф цього відношення не має петель або контурів, і за означенням відношення досяжності .¨

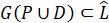Якщо відношення Р сумісне зі строгим порядком D та компоненти всіх пар (х,у)ÎР належать до X (х, у Î X), де X Ì А, то відношення Р сумісне зі строгим порядком, який є звуженням відношення D на підмножину X. Справедливе й обернене твердження.

ТЕОРЕМА 2.1 (про сумісність). Нехай D – відношення строгого порядку, Р – бінарне відношення (обидва з носієм А), й елементи пар (х,у)ÎР належать підмножині XÌА. Якщо відношення Р сумісне зі строгим порядком, що є звуженням відношення D на підмножину X, то відношення Р сумісне зі строгим порядком D.

Позначимо множину всіх відношень строгого порядку з носієм А як W(A). Множина W(A) впорядкована за відношенням теоретико–множинного включення, оскільки елементи відношення є множинами. Більше того, відношення строгого порядку D з носієм А є мажорантою тоді й лише тоді, коли воно не міститься в жодному іншому відношенні порядку з носієм А. Теорема про сумісність має важливий наслідок.

ТВЕРДЖЕННЯ 2.21 (наслідок теореми про сумісність). На впорядкованій множині всіх відношень строгого порядку з носієм А лінійні відношення строгого порядку й лише вони є мажорантами.

Доведення. Припустімо, що для лінійного відношення строгого порядку D з носієм А знайдеться таке відношення строгого порядку R з носієм А, що DÌR. Тоді існують такі х, у Î А, що xRy та (х, у) Ï D. Крім того, оскільки відношення D – лінійне, то yDx, а з DÌR випливає yRx, що суперечить припущенню про те, що xRy. Це означає, що не існує відношення строгого порядку, яке включало б D.

Припустімо, що мажоранта D впорядкованої множини – не лінійне відношення. Тоді знайдуться такі х, у Î А, що (х, у) Ï D й (у, х) Ï D. У цьому разі бінарне відношення Р{(х, у)} сумісне зі строгим порядком, що є звуженням відношення D на підмножину {х, у}. Згідно з теоремою про сумісність відношення Р сумісне зі строгим порядком D, тобто існує таке відношення строгого порядку R із носієм А, що 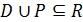. Оскільки хРу, то й xRy та (х, у) Ï D відповідно до початкового припущення про нелінійність D. Тому виконується строге включення D Ì R. Це означає, що нелінійне відношення не може бути мажорантою в .

Наведені теоретичні результати дають змогу довести одну з основних теорем про бінарні відношення.

ТЕОРЕМА 2.2 (теорема Шпільрайна). Для довільного відношення строгого порядку D з носієм А знайдеться таке лінійне відношення строгого порядку R з носієм А, що D Ì R. Інакше кажучи, кожен строгий порядок можна продовжити до лінійного строгого порядку.

Доведення. Застосуємо лему Цорна до впорядкованої множини . Якщо – ланцюг відношень строгого порядку з носієм А (І – множина індексів відношень строгого порядку), то – також відношення строгого порядку з носієм А.

Отже, на впорядкованій множині кожен ланцюг має мажоранту, тобто ця множина індуктивна. За лемою Цорна довільне відношення строгого порядку має мажоранту – максимальне за включенням відношення строгого порядку. Згідно з наслідком теореми про сумісність максимальність відношення строгого порядку означає його лінійність.

Із теорем про сумісність та Шпільрайна випливає таке твердження.

ТВЕРДЖЕННЯ 2.22. Довільне лінійне довпорядкування підмножини впорядкованої множини можна продовжити до лінійного впорядкування всієї впорядкованої множини. Якщо X – дискретна підмножина впорядкованої множини 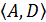і в множині X існують непорівняльні за звуженням відношення D на підмножину X елементи, то довпорядкування множини X до лінійного строгого порядку можна продовжити до лінійного впорядкування всієї множини А.

Наведені теоретичні результати обґрунтовують можливість приймати рішення в декілька етапів. Спочатку, виходячи зі сталої інформації про переваги, без втручання децидента виділяють підмножину наявних альтернатив, які відповідають певному синтезованому принципу вибору. Остаточний вибір (або довпорядкування, якщо розв’язком задачі прийняття рішення має бути лінійний строгий порядок) виконує безпосередньо децидент (якщо потужність отриманої на першому етапі підмножини порівняно невелика) чи це триває декілька етапів з конкретизацією переваг на наявній підмножині.

Зручною є змістовна інтерпретація теореми Шпільрайна за допомогою поняття нумерації.

Нумерацією n–елементної впорядкованої множини А, n = саrd(A), яка є носієм відношення строгого порядку D називається взаємно однозначне (ізоморфне) відображення множини А на множину N = {1, 2, ..., n}, причому «кращому», чи «більшому», ніж уÎА елементу хÎА (xDy) відповідає більше значення іÎN. Отже, нумерацію елементів множини А можна розглядати як розташування їх у вигляді послідовності {х, у, ..., z}, ізоморфним образом якої є послідовність {1, 2, ..., n]. При цьому виконується умова 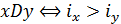, де і_x, і_у – номери елементів х та у у послідовності {1, 2, ..., n).

Для скінченної впорядкованої множини 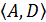нумерація еквівалентна побудові лінійного довпорядкування R порядку D.

Зручний і наочний спосіб подання впорядкованих множин – діаграми Гассе. На них кожен елемент зображено точкою площини. Якщо елемент у домінує над х, то точки х та у сполучають відрізком, причому точка, що відповідає елементу х, має бути нижче за у. Діаграму Гассе будують так. Елементи множини А зображують точками площини, причому для таких елементів х, у Î Р, що хРу, точка, що відповідає елементу х, знаходиться вище, ніж та, що відповідає елементу у, і ці точки треба з’єднати відрізком. Отже, якщо в діаграмі в напрямку руху «вниз» є шлях від х до z, то xPz. Дуг, що відображають транзитивність відношення Р не наводять.

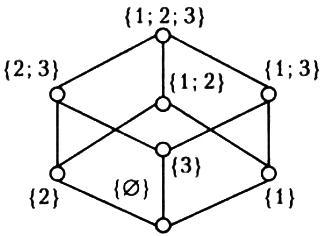
Приклад 2.28. Нехай А = {1, 2, 3}. На множині всіх підмножин множини А розглянемо відношення «бути підмножиною». Діаграму цієї впорядкованої множини наведено на рис. 2.11.

Рис. 2.11. Діаграма Гассе для прикладу 2.28	Рис. 2.12. Діаграма Гассе для прикладу 2.29

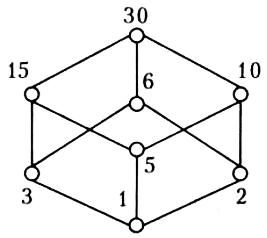
Приклад 2.29. Нехай А = {1, 2, 3, 5, 6, 10, 15, 30}. Задамо на цій множині відношення «ділиться». Діаграму цієї впорядкованої множини наведено на рис. 2.12.

Діаграми Гассе для цих відношень збігаються. Це означає, що ці частково впорядковані множини мають однакову структуру, тобто є ізоморфними.

Приклад 2.30. Нехай відношення строгого порядку D з носієм А = {х₁, х₂, х₃, х₄, х₅, х₆) задано матрицею

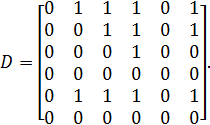
Побудуємо для нього граф (рис. 2.13) і діаграму Гассе (рис. 2.14)/

Рис. 2.13. Граф відношення строгого порядку для прикладу 2.30	Рис. 2.14. Діаграма Гассе для прикладу 2.30

На діаграмі х₁, та х₅ можна розмістити довільно одне відносно іншого, так само як х₆ щодо х₃, х₄,. Відношення Р можна продовжити до строгого порядку кількома способами:

(х₁, х₅, х₂, х₆, х₃, х₄), (х₁, х₅, х₂, х₃, х₆, х₄), (х₁, х₅, х₂, х₃, х₄, х₆),

(х₅, х₁, х₂, х₆, х₃, х₄), (х₅, х₁, х₂, х₃, х₆, х₄), (х₅, х₁, х₂, х₃, х₄, х₆).

Існують алгоритми пошуку всіх довпорядкувань до строгого порядку, однак ця проблема має скоріше теоретичний інтерес, оскільки в ході прийняття рішення нас цікавить таке довпорядкування, яке найкраще б відповідало системі переваг децидента.

Отже, виникає проблема побудови довпорядкування, яке б було в певному сенсі «найближчим» до системи переваг децидента. Для цього призначені спеціальні принципи вибору найкращого рішення. Алгоритм отримання найкращого з погляду децидента рішення може бути багатоетапним: спочатку задають напівпорядок на множині варіантів рішень, а потім, послідовно звужуючи множину варіантів або наближуючи кожне наступне бінарне відношення до строгого порядку, обирають найкращий варіант.

Структури «домінування – байдужість»

Читайте також:

1. IV. Прийняття рішень у полі четвертої інформаційної ситуації
2. V. Прийняття рішень у полі п’ятої інформаційної ситуації
3. VI. Прийняття рішень у полі шостої інформаційної ситуації
4. Аналіз альтернативних рішень
5. Аналіз для прийняття рішень стосовно залучення інвестицій
6. Аналітичні методи та інструменти підтримки прийняття управлінських рішень.
7. Багатоаспектний підхід до прийняття управлінськихрішень
8. Багатоцільова багатокритеріальна модель обґрунтування рішень в полі кількох інформаційних ситуацій
9. База управлінських рішень і закони організації.
10. Бюджетні множини й лінії бюджетного обмеження
11. Вибір місця розташування підприємства як проблема прийняття рішень.
12. Вибір управлінських рішень

Переглядів: 2895