• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Властивості факторизованих відношень

Розглянемо питання про збереження властивостей первісних відношень у разі їх факторизації за довільною еквівалентністю. Зазначену проблему розв’язують такі твердження.

ТВЕРДЖЕННЯ 2.12. Властивість рефлексивності зберігається в разі факторизації.

Доведення. Нехай Р – рефлексивне відношення з носієм A, D – відношення еквівалентності, А_i – довільний клас еквівалентності за відношенням D. Оскільки А_i ¹ Æ, то знайдеться хоча б один елемент хÎ А_i. Унаслідок рефлексивності відношення Р справедливе твердження хРх, і за означенням фактор–відношення А_iP_DA_i. ¨

ТВЕРДЖЕННЯ 2.13. Властивість симетричності зберігається в разі факторизації.

Це твердження можна довести аналогічно до попереднього. Що стосується властивості транзитивності, то, узагалі кажучи, вона не зберігається в разі факторизації. Необхідні та достатні умови її збереження дають наступні твердження.

ТВЕРДЖЕННЯ 2.14 (достатня умова збереження транзитивності фактор–відношення). Властивість транзитивності зберігається в разі факторизації транзитивного відношення за відношенням еквівалентності, що міститься в первісному відношенні.

Доведення. Нехай Р – транзитивне відношення, D – відношення еквівалентності з тим самим носієм A, D Ì Р. Розглянемо три довільні класи еквівалентності A_i, A_j, А_k за відношенням D такі, що A_iР_DA_j, A_jР_DA_k, де P_D – фактор–відношення, отримане факторизацією первісного відношення Р за еквівалентністю D. Тоді знайдуться такі елементи х_lÎA_i, х_m, х_nÎA_j, х_рÎA_k, для яких х_lРх_m, х_nРх_р (за означенням фактор–відношення). Оскільки х_m та х_n належать до одного класу еквівалентності, то х_mDx_n, із D Ì Р випливає х_mРх_n. Отже, x_lPx_m, x_mPx_n, х_nРх_р і, унаслідок транзитивності відношення Р, х_lРх_р (якщо клас A_j складається з одного елемента х_m, то бажаний результат одержимо безпосередньо з умови транзитивності відношення Р). За означенням фактор–відношення маємо A_jР_DA_k.

ТВЕРДЖЕННЯ 2.15. Необхідна та достатня умова транзитивності відношення P_D в разі факторизації довільного бінарного відношення Р за довільною еквівалентністю D, що мають спільний носій А, є виконання умови

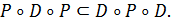
ТВЕРДЖЕННЯ 2.16. Властивість лінійності зберігається в разі факторизації.

Це твердження можна перевірити безпосередньо.

ТВЕРДЖЕННЯ 2.17. Факторизація відношення квазіпорядку за його симетричною складовою є відношенням порядку.

Доведення. Нехай Р – відношення квазіпорядку з носієм 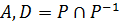– його симетрична складова. Згідно з твердженням 2.9, D – відношення еквівалентності з носієм А. Фактор–відношення P_D рефлексивне відповідно до твердження 2.12. Оскільки D Ì Р та відношення Р транзитивне за означенням квазіпорядку, то відношення P_D транзитивне твердження 2.14. Доведемо, що P_D – антисиметричне відношення. Оскільки відношення Р транзитивне та D Ì Р, то Р транзитивне відносно D, тобто справедливі твердження хРу, yDz, xPz, xDy, yPz, xPz, де x,у,zÎА. Отже, для такої довільної пари х,уÎА, що хРу, належність її до відношення Р не змінюється після заміни її компонентів елементами, еквівалентними за відношенням D. Щоб з’ясувати, чи належить довільна пара класів еквівалентності А_i, A_j до фактор–відношення P_D, обираємо довільні елементи х та у із цих класів: хÎA_i, уÎA_j. У цьому випадку A_iP_DA_j тоді й лише тоді, коли хРу.

Припустімо, що відношення P_D симетричне. Тоді A_iP_DA_j і A_jP_DA_i, тобто згідно з попереднім із хРуÙуРх випливає , що суперечить припущенню про належність елементів х та у до різних класів еквівалентності А_i й А_j. Отже, P_D є антисиметричним відношенням, а також порядком, тому що воно має властивості рефлексивності та транзитивності.

Із твердження 2.17 випливає, що в разі факторизації квазіпорядку за симетричною складовою зберігається лінійність.

Приклад 2.26. Розглянемо відношення Р (рис. 2.7)

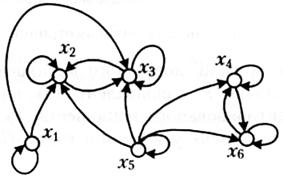Рис. 2.7. Граф відношення Р

Неважко перевірити, що Р² = Р, а тому транзитивне замикання

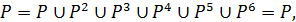
тобто відношення Р транзитивне. Оскільки воно ще й рефлексивне, то є квазіпорядком. Виділимо його симетричну складову:

Відношення D – еквівалентність, а тому розбиває множину–носія А = {х₁, х₂, х₃, х₄, х₅, х₆} на чотири класи A₁ = {х₁}, А₂ = {х₂, х₃}, А₃ = {х₄, х₆}, А₄ = {х₅}. Факторизуємо відношення Р за відношенням D. Носій фактор–відношення P_D – множина А_D = {А₁, А₂, А₃, A₄}. На рис. 2.8 показано граф відношення Р з класами еквівалентності за відношенням D.

Рис. 2.8. Граф відношення Р з класами еквівалентності за відношенням D

Матриця відношення P_D має вигляд

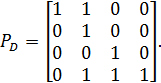
На рис. 2.9 показано його граф.

Рис. 2.9.Граф G(P_D) факторизованого відношення Р_D

Відношення P_D — рефлексивне, транзитивне та антисиметричне, тобто є порядком.

Розглянемо результати факторизації довільного відношення Р за його відношенням взаємної досяжності 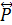. Оскільки 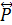– еквівалентність, класи якої є контурами в графі G(P), то граф факторизованого відношення не має контурів. Контури, що були в графі G(P), «стягнулись» у вершини графа . Про це йдеться в наступному твердженні.

ТВЕРДЖЕННЯ 2.18. Факторизація довільного відношення Р за його відношенням взаємної досяжності 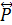дає ациклічне фактор–відношення.

Із цього твердження випливає важливе твердження 2.19.

ТВЕРДЖЕННЯ 2.19. Якщо Р – лінійне відношення з носієм А, то фактор–відношення , отримане з Р шляхом факторизації його за відношенням взаємної досягальності, є лінійним відношенням порядку з носієм .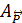

Доведення. Згідно з твердженням 2.18 фактор-відношення ациклічне. Позаяк властивість лінійності зберігається в разі факторизації, то воно лінійне, а відповідно до твердження 2.14 – транзитивне. Оскільки з ациклічності випливає антисиметричність, то відношення саме таке. Крім того, внаслідок лінійності відношення воно також є рефлексивним.¨

Отже, факторизація довільного відношення за відношенням взаємної досяжності дає фактор–відношення без контурів, тобто в процесі такої факторизації відбувається «стягування» контурів первісного бінарного відношення [49]. Факторизація – це, по суті, агрегування системи переваг децидента, що дає змогу досліджувати загальні властивості системи переваг і корегувати отримане відношення.

Читайте також:

1. Аеродинамічні властивості колісної машини
2. Аналізатори людини та їхні властивості.
3. Аналізатори людини та їхні властивості.
4. Атрибутивні ознаки і властивості культури
5. Білки, властивості, роль в життєдіяльності організмів.
6. Біосфера Землі, її характерні властивості
7. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
8. Будова і властивості аналізаторів
9. Векторний добуток і його властивості.
10. Вибір кращих альтернатив за допомогою бінарних відношень
11. Види і властивості радіоактивних випромінювань
12. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).

Переглядів: 2393