• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Відповідності

Відповідність між множинами X і Y - це трійка множин q = ( X,Y,Q ), , де X – множина, елементи якої зіставляються з елементами іншої множини, Y – множина, з елементами якої зіставляються елементи першої множини, (- множина, що визначає закон, відповідно до якого здійснюється відповідність, тобто перераховуються все пари елементів (х, у), що беруть участь у зіставленні).

Часто відповідністю між множинами Х та Y називають тільки множину Q , що є підмножиною декартового добутку , тобто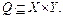

Якщо (х,у), то говорять, що елемент у відповідає елементу х. Геометрично це зображується стрілкою, спрямованою від х до у.

Область визначення ( множина відправлення ) відповідності - множина 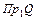. У неї входять елементи множини Х , які беруть участь в зіставленні.

Всюди (повністю ) визначена відповідність: якщо .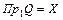

Частково визначена - у противному випадку.

Область значень (множина прибуття) відповідності - множина 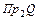(містить елементи множини Y, які беруть участь у зіставленні).

Сюр’єктивною відповідність: якщо .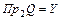

Образ елемента х у множині Y при відповідності q (або Q) - множина всіх елементів , що відповідають елементу .

Прообраз елемента у у множині Х при відповідності q (або Q) - множина всіх елементів , яким відповідає елемент .

Приклад.Нехай дані дві множини : Х = {1, 2, 3} і Y = {e, f, g }.

□ На мал. 1.3 показана відповідність між цими множинами. Q=, що є підмножиною прямого добутку

Область визначення цієї відповідності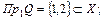область значень . Рис. 1.3

Елемент e–образ елементів 1,2 у множині Y при відповідності Q; елементи 1,2 – прообрази елемента e у множині Х при відповідності Q. Тому що не всі елементи множини Х входять в область визначення, то дана відповідність є частково визначеною.

Приклад усюди визначеної відповідності показаний на мал. 1.4

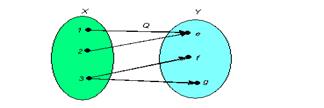
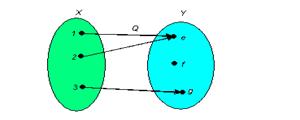
Рис. 1.4 Рис. 1.5

Тут всі елементи множини Х беруть участь у зіставленні.

Приклад сюр’єктивної відповідності показаний на мал. 1.5. Тут всі елементи множини Y беруть участь у зіставленні. Цей малюнок описує відповідність Q = , . ■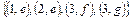

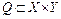Приклад.Нехай Х = {1, 2}, Y = {3, 5}. Розподіл елементів множини Х по елементах множини Y є відповідність. Визначити всі можливі відповідності, їхні області визначення і області значень.

□ Для знаходження відповідностей необхідно визначити декартовий добуток заданих множин:

Одержали множину, що складається із чотирьох двоелементних кортежів. Одним з можливих відповідностей може бути відповідність елемента 3 із множини Y елементу 1 із множини Х , тобто 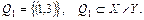Тоді ми одержимо відповідність (трійку множин) 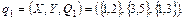Областю визначення відповідності q₁ є , а областю значень q₁ є

Як уже говорилося, за відповідність можна взяти не трійку множин q , а множину Q , що є підмножиною прямого добутку множин X і Y. У цьому випадку запис буде коротше. Вибираючи , ми одержимо всі можливі відповідності і їхні області визначення й області значень :

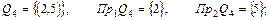
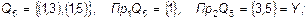
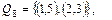
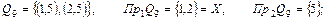
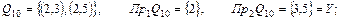
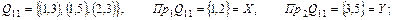
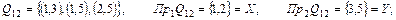
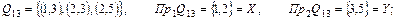
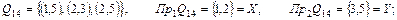
Q₁₆ = {Ø}, Пр₁Q₁₆ = {Ø}, Пр₂Q₁₆ = {Ø} .

У випадках, коли Пр₁Q_I = X, відповідність визначена всюди. Якщо Пр₂Q_I =Y, то відповідність є сюр’єктивною.■

Функціональна (однозначна ) відповідність q (або Q): образом будь-якого елемента з області визначення відповідності є єдиний елемент із області значень.

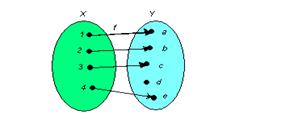
Ввзаємно однозначнавідповідність q (або Q ): всюди визначена, сюр’єктивна, функціональна, і, крім того, прообразом будь-якого елемента з області значень є єдиний елемент із області визначення відповідності. Рис. 1.6

На мал. 1.3 і 1.4 показані функціональні відповідності. При цьому відповідність, зображена на мал. 1.3, є частково визначеною функціональною відповідністю, а відповідність, показана на мал. 1.4, є всюди визначеною функціональною відповідністю. Відповідність, зазначена на мал. 1.5 не є функціональною, тому що елемент 3 з області визначення відповідності має два образи f і g з області значень відповідності. Приклад взаємно однозначної відповідності показаний на рис.1.6.

Нескінченні множини:

Рівнопотужні множини М₁ і М₂ (позначають |М₁|=|М₂|): якщо між елементами встановлена взаємно однозначна відповідність.

Злічена множина: рівно потужна множині натуральних чисел N.

1. будь-яка нескінченна підмножина N є зліченою;

2. об'єднання кінцевого числа злічених множин є зліченим;

3. об'єднання зліченої множини кінцевих множин також злічене.

Множина всіх дійсних чисел відрізка [0, 1] не є зліченою.

Континуальна множина або континуум - незліченна множина. Потужність незліченної множини називають континуумом.

Функція f - це функціональна відповідність 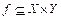(де кожному елементу х з області визначення Х ставиться у відповідність єдиний елемент у з області значень Y). Це можна позначити записом y = f(x). Елемент х – аргумент функції, у – значення функції.

Відображення Х у Y - повністю визначена функція f, позначається

У цьому випадку кожний елемент має тільки один образ y = f(x) з Y.

Відображення Х на Y(сюр’єкція або накриття): якщо будь-який елемент - образ, принаймні, одного елемента (тобто, відповідність повністю визначена і сюр’єктивна).

Ін’єктивне відображення(ін'єкцієя): якщо для будь-яких двох різних елементів х₁ і х₂ з Х їхні образи й також різні.

Бієкція (накладення взаємно однозначне відображення)- відображення, що є одночасно сюр’єктивним і ін’єктивним. У цьому випадку кажуть, що між елементами множин X і Y є взаємно однозначна відповідність.

Тому що відображення є функцією, то функцію можна записати у вигляді

Читайте також:

1. Визначати ступінь відповідності обраної регресії відображуваним на діаграмі даним.
2. Групи та критерії відповідності для права перебувати на спрощеній системі
3. Дуже успішні підприємства скеровують свою діяльність у відповідності з деякими основними цінностями та переконаннями, які знайшли відображення в девізах.
4. Знайдіть помилки у відповідності букв і цифр і виправте їх (А-…,Б-…,): вказати цифру помилкової ідеї
5. Знак відповідності або якості
6. Знаки відповідності ситеми УкрСЕПРО
7. Ідеї народності та природовідповідності Григорія Сковороди.
8. Координування – це встановлення узгодженості дій численних виконавців плану у відповідності до цілей підприємства.
9. Лекція №10. Документування вимог у відповідності зі стандартами
10. Малюнок № 1.20. Граф відповідності.
11. Організація інформаційних систем у відповідності до стандарту МPР II

Переглядів: 2509