
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Мера информации источника непрерывных сообщений
Источник сообщений, имеющих непрерывное вероятностное распределение в дискретизованом виде с шагом дискретизации  имееет энтропию
имееет энтропию
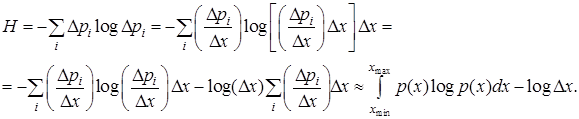
 |
Здесь i – номер интервала дискретизации, под вероятностным распределением понимается плотность вероятностей
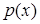 распределения случайной величины, которая является сигналом, или несет информацию.
распределения случайной величины, которая является сигналом, или несет информацию.
Равномерное распределение
характеризуется энтропией
 .
.
Под дифференциальной энтропией понимается величина
 ,
,
или при условии 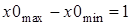
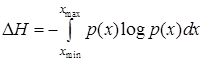 .
.
Таким образом, величина 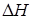 интерпретируется как разность между энтропией анализируемого распределения и энтропией равномерного распределения на единичном интервале и как величина относительная может принимать произвольные значения.
интерпретируется как разность между энтропией анализируемого распределения и энтропией равномерного распределения на единичном интервале и как величина относительная может принимать произвольные значения.
Задача1 Визначити ентропію джерела повідомлень з m літер алфавіта, вважаючи, що загальна кількість літер в алфавіті дорівнює k і всі повідомлення рівноймовірні.
Розв‘язання Загальне число повідомлень складає п=km, таким чином ентропію джерела повідомлень визначаємо, як
Н(Х) =logn= m logk
Задача 2 Колода міститьп = 32 карти. З неї випадковим чином вилучається одна. Яка кількість інформації міститься у відповіді на запитання: “Чи є вилучена карта тузом?” Чому дорівнює середня ентропія закритої карти? За яке мінімальне число запитань, на які дається відповідь “так” чи “ні” можна гарантовано встановити карту? Як потрібно ставити питання, щоб їх кількість була мінімальною?
Розв‘язання Кількість інформації, що міститься у відповіді на запитання: “Чи є вилучена карта тузом?” становить I= – log(4/n) = 3 біт , якщо карта дійсно є тузом таI= – log(1–4/n) = 0.193 біт інакше. Ентропія закритої карти, або інформація яка дається відкриттям карти, дорівнюєН(Х) = logn =.5 біт. Максимальна інформація, що гарантовано дається відповіддю з двома наслідками “так” чи “ні” складає I0 = log2 =1 біт, тобто гарантовано встановити карту можна за q = Н(Х)/I0 = logn/log2 = 5. Щоб кількість запитань була мінімальною і кожна відповідь гарантовано несла інформацію ровно в 1 біт, необхідно, щоб кожне питання відносилося до однієї з двох підгруп однакового об’єму, наприклад: “Чи є карта червоною?”
Задача 3 Ймовірність того, що випадково обраний мешканець міста є студентом, складає Р(А), ймовірність того, що випадково обраний мешканець є юнаком – Р(В). Ймовірність того, що мешканець – юнак при умові, що він студент – Р(В/А).Скількі інформації несе повідомлення, що випадково обраний юнак є студентом?
Розв‘язання Визначимо ймовірність того, випадково обраний мешканець міста є студентом при умові, що він юнак Р(А/В). Ймовірність того, випадково обраний мешканець міста є одночасно студентом і юнаком
Р(АВ) = Р(А/В) Р(В) = Р(B/A) Р(А)
Тоді Р(А/В) =Р(B/A) Р(А)/Р(В). Повідомлення, що випадково обраний юнак є студентом несе інформацію
I= – logР(A/B)= – log[Р(B/A)P(A)/P(B)]
Задача 4 Знайти диференціальну ентропію експоненціального розподілу.
Розв‘язання
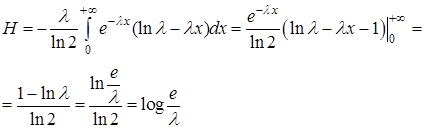
Ентропія складного дискретного повідомлення
Теоретичні положення Найпростіше складне повідомлення {хi уj}i=1,…,п; y=1,..,m складається з двох простих повідомлень {хi}i=1,…,пта {уj} y=1,..,m . Ентропія джерела такого повідомлення визначається як
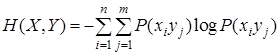
Властивості складної ентропії:
- H(X,Y)=H(Y,X);
- H(X,Y)£ H(X)+H(Y), при чому H(X,Y)= H(X)+H(Y), якщо прості повідомлення, що входять до складного статистично незалежні, тобто Р(хi уj)= Р(хi)Р(yj).
Задача Привести таблицю двовимірного ймовірностного розподілу наслідків кидання двох монетР(хi уj). Знайти ентропію джерела інформації, що характеризується таким розподілом.
Розв‘язання Наслідки кидання першої монети {хi}i=1,…,2={Г,Р} та другої
{уj} y=1,..,2={Г,Р}, деГ – герб, Р– решка. Ці наслідки рівноймовірні і ймовірність будь-якого наслідка складає 0.5. Оскільки ці наслідки статистично незалежні, таблиця двовимірного ймовірностного розподілу наслідків кидання двох монетР(хi уj) має вигляд
| хi | Г | Р |
| уj | ||
| Г | 0.25 | 0.25 |
| Р | 0.25 | 0.25 |
Ентропію джерела інформації, що характеризується таким розподілом складає

Що дорівнює 2 біт.
Умовна ентропія дискретного повідомлення
Теоретичні положення Умовною ентропією джерела Yпри відомому стані джерела X зветься величина

Властивості умовної ентропії
- H(Y/X)=H(X,Y) – H(X);

- H(X/Y)=H(X,Y) – H(Y);
- H(Y/X) ³ 0, при чому H(Y/X) = 0 якщо повідомлення Y та X повністю статистично залежні;
- H(Y/X) £ H(Y), при чому H(Y/X) = H(Y) якщо повідомлення Y та X статистично незалежні.
Таким чином, з останньої властивості з урахуванням властивості простої ентропії випливає, що ентропія джерела інформації максимальна, якщо його повідомлення рівно ймовірні та статистично незалежні.
При наявності кореляційних зв’язків між трьома повідомленнями, умовна ентропія джерела визначається рівнянням
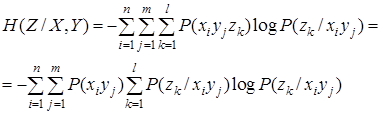
Вважаючи, що російський алфавіт містить 32 символи, при умові рівноймовірності і відсутності статистичної залежності їх появи, кожний символ ніс би 5 біт інформації, але врахування нерівноймовірності знижує цю величину до 4.39 біт, а кореляційних залежностей між двома, трома та восми символами – відповідно до 3.52, 3.05 та 2 бітів.
Задача Сигнал формується у вигляді двійкового кода з рівнями повідомлень x0та x1з умовними ймовірностями появи повідомлень Р(x0/x0), Р(x1/x1), Р(x0/x1), Р(x1/x0). Знайти безумовні ймовірності появи повідомлень, середню ентропію джерела сигналу, якщо його початковий стан невідомий і його умовну ентропію, якщо початковий стан відомий.
Зауваження Умовні ймовірності повинні задовольняти співвідношенням:
Р(x0/x0) + Р(x1/x0) = 1;
Р(x1/x1) + Р(x0/x1) = 1.
Розв‘язання Безумовні ймовірності появи повідомлень Р(x0)та Р(x1) визначаються з системи рівнянь
Р(x0) + Р(x1)=1;
Р(x0) = Р(x0/x0)Р(x0)+Р(x0/x1)Р(x1)/
З другого рівняння випливає, що
[1 – Р(x0/x0)]Р(x0)=Р(x0/x1)Р(x1)
або Р(x1/x0) Р(x0) =Р(x0/x1)Р(x1). Підставляючи це співвідношення в перше рівняння остаточно маємо
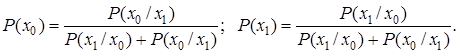
Середня ентропя джерела сигналу, якщо його початковий стан невідомий, становить
і його умовна ентропія, якщо початковий стан відомий

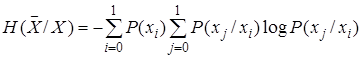
Читайте також:
- Кодирование информации
- ПОНЯТИЕ ИНФОРМАЦИИ. НОСИТЕЛИ ИНФОРМАЦИИ
- Протокол надійної доставки TCP-сообщений
- Требования, предъявляемые к аналитической информации.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Вступ. Загальна рецептура. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |