• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Факторизація

Факторизація

Сформулюємо задачу факторизації або розкладу на прості множники натурального числа.

Задано: п N (п > 1).

Знайти: прості р₁,... ,р_s, і натуральні 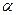₁,..., 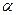_s такі, що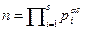

Зазначимо, що факторизація натурального числа, тобто задача пошуку всіх його простих дільників, еквівалентна задачі пошуку хоча б одного простого дільника (див приклад ІІІ,4.3) Слід також відзначити, що ефективні тести простоти із попереднього параграфу хоча й дозволяють швидко розпізнати, складеним чи простим є задане число, але не дають жодної інформації про дільники складеного числа.

На сьогоднішній день задача факторизації є важкою. Найефективніші з відомих алгоритмів факторизації, включно з ймовірнісними, потребують часу

, (1)

причому у найкращому випадку с = 1. Є також алгоритми з оцінкою часу

(2)

яка не доведена, а припускається на основі деяких евристичних міркувань.

На межі сучасних можливостей є факторизація чисел із 150 десятковими цифрами. Розклад на множники чисел, які мають 200 десяткових цифр, на думку експертів, залишається справою майбутнього.

Для зламу деяких криптосистем суперникові досить розкласти на множники число п, про яке відомо, що воно є добутком двох простих. Тобто виникає звужена задача факторизації.

Задано: п — pq, де р і q прості.

Обчислити: р і q.

Для звуженої задачі невідомо нічого кращого, ніж у загальному випадку. Однак деякі алгоритми факторизації досягають успіху, якщо р і q задовольняють певні умови. Сформульовано властивості, які виключають виконання цих небажаних умов. Прості числа, що володіють цими властивостями, називаються сильно простими. Спосіб їх породження запропоновано в [102].

Цікаво також зауважити, що для розпізнавання, чи натуральне число є добутком рівно двох простих, невідомо кращого способу, ніж безпосередня факторизація.

ВПРАВИ

3.1. а) Розробити метод факторизації чисел вигляду п = pq, де р і q — прості числа-близнята, тобто q = р + 2.

b)Розробити метод факторизації чисел вигляду п = pq для простих р і q, ефективний у випадку, коли різниця q — р невелика. (Спосіб, викладений у розділі розв'язків, називається факторизацією Ферма.)

3.2.([1Н]) а) Нехай для п відомо таке х , що п є псевдопростим, але не сильно псевдопростим за основою х. Вказати спосіб швидкого знаходження нетривіального дільника числа п.

b)Пояснити, як слід вибирати прості р і q, щоб число п = pq було важко факторизувати шляхом знаходження х як у пункті ь.

ЛІТЕРАТУРА

За детальнішою інформацією про алгоритми факторизації слід звертатися до оглядів [42, 114, 64], підручника [111] та монографії [32, розділ 4.5.4].

Читайте також:

1. Агрегування та факторизація

Переглядів: 1320