Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розпізнавання квадратичності і добування квадратних коренів

4.1. Квадратичнiсть у випадку простого модуля.Насамперед ми розглянемо задачу

розпізнавання квадратичних лишків за простим модулем

Задано: х, р N, де р > 2 просте і р† х.

Розпізнати: чи існує у таке, що ху² (mod p) ?

Очевидно, що задача еквівалентна обчисленню символа Лежандра (), яке можна виконати двома способами. Перший полягає у використанні критерію Ойлера, за яким

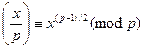
При цьому права частина ефективно обчислюється за допомогою бінарного методу піднесення у

степінь за модулем (пункт III.2.2). Другий спосіб полягає у трактуванні 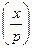як символу Якобі і використанні алгоритму із пункту 1.2 для обчислення останнього.

Нагадаємо, що через Q_p позначається множина зведених квадратичних лишків, тобто множина квадратичних лишків в . Випадковий елемент множини Q_p породжується легко — досить взяти випадковий елемент в і піднести його до квадрату за модулем р. Дещо складніше вибрати в випадковий квадратичний нелишок. Для цього вибираємо випадковий елемент в і перевіряємо одним із двох згаданих вище способів, є він нелишком, чи ні. Якщо нам не пощастило, то ще раз вибираємо елемент в випадково і незалежно від попереднього вибору, і перевіряємо, чи не виявиться нелишком

він. Так продовжуємо, поки не натрапимо на нелишок. Оскільки квадратичних лишків та нелишків в однакова кількість (див. вправу 1.9), то ймовірність вибору нелишка дорівнює 1/2. Отже, ймовірність того, що ми не знайдемо нелишок упродовж k ітерацій, дорівнює 2^-^k. Обчислення, подібні до проведених у пункті III.3.2, показують, що математичне сподівання кількості потрібних ітерацій дорівнює 2.

Тепер сформулюємо задачу знаходження квадратичного нєлишка (не обов'язково випадкового) в явному вигляді.

знаходження квадратичного нелишка за простим модулем

Задано: просте р.

Знайти: х\Q_p.

Ми вже описали для цієї задачі поліноміальний Лас Вегас алгоритм із ймовірністю невдачі 1/2, яку можна зменшити до 2^-^kповторенням алгоритму k разів. Детермінованого поліноміального алгоритму для цієї задачі невідомо.

4.2. Добування квадратного кореня за простим модулем. Наступною ми розглянемо задачу

добування квадратного кореня за простим модулем

Задано: х, рN, де р > 2 просте і р† х.

Знайти: у таке, що хy²(mod ), якщо існує.

Для цієї задачі поліноміальний детермінований алгоритм відомий лише за справедливості РГР. Нижче подається поліноміальний ймовірнісний алгоритм.

Оскільки квадратичність за простим модулем розпізнається ефективно, ми можемо обмежитись випадком, коли х є квадратичним лишком за модулем р. У наступних двох часткових випадках задача легко розв'язується детермінованим чином.

Випадок 1: р = 4т + 3.

За критерієм Ойлера маємо х^2т+1 1 (mod p), звідки (x ^m⁺¹)² x (mod p). Таким чином, можна взяти
y = ± х^т+1 (mod p) (це обидва корені з х в ).

Випадок 2: р = 8т + 5.

За критерієм Ойлера маємо x⁴^m⁺² 1 (mod p), звідки x²^m⁺¹ ±1 (modp) і x²^m⁺² = ± x(mod p). Який саме знак має місце у правій частині останнього порівняння, можна визначити безпосереднім обчисленням x²^m⁺¹ mod р за допомогою бінарного методу. Якщо права частина виявиться рівною +1, то діємо як у випадку 1. Якщо ж у правій частині маємо —1, то використовуємо пункт 2 квадратичного закону взаємності Гауса, за яким (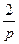) = -1 і, знову за критерієм Ойлера, 2⁴^m⁺² = -l(mod p). Тому маємо _Х^2т+22⁴^т⁺² x (mod p),i y=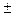x²^m⁺¹2²^m⁺¹mod p. Залишився

Випадок 3: р = 8m + 1.

Опишемо, як у цьому випадку добувати квадратний корінь, якщо додатково відомо квадратичний нелишок а за модулем р. Цим ми зведемо нашу задачу до знаходження квадратичного нeлишка за простим модулем, для чого у попередньому пункті була вказана ймовірнісна процедура. Це єдине місце в алгоритмі, де використовується випадковість.

Нехай р=2^lh + 1,деl3іh непарне. За критерієм Ойлера маємо 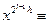1(mod p) , звідки 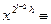±1 (mod p). Застосувавши критерій Ойлера до квадратичного нeлишка а, отримаємо 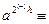-1 (mod p). З останніх двох порівнянь для деякого цілого s₁, рівного 0 або h, випливає

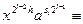1 (mod p) , 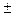1 (mod p)

З останнього порівняння таким же чином для деякого цілого невід'ємного s₂ отримуємо

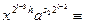1 (mod p) ,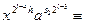 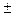1 (mod p)

Повторивши подібну процедуру ще l - 3 рази, приходимо до порівняння 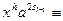1 (mod p) для деякого цілого невід'ємного s_l_-1, звідки остаточно отримуємо

y = ±mod p

4.3. Випадок модуля п = pq. Цей пункт присвячено двом задачам.

розпізнавання квадратичних лишків за модулем n = pq

Задано: х, пN. ri = pq для різних непарних простих р і q, НСД (х, n) = 1.

Розпізнати: чи існує у таке, що хy²(mod n) ?

добування квадратного кореня за модулем п = pq

Задано: х, п N, п = pq для різних непарних простих р і q, НСД (х, п) = 1.

Знайти: у таке, що ху² (mod п), якщо існує.

Слід підкреслити, що співмножники р і q не задаються в умові задачі. За умовою відомо лише, що п єдобутком двох простих чисел, але самі ці числа невідомі, а їх визначення за n є важкою задачею (див. § 3). твердження 4.1. Нехай п = рq є добутком двох різних непарних простих чисел. Припустимо, що число х взаємно просте з п, і позначимо х₁ = х mod p, x₂=x mod q. Тоді мають місце такі факти.

1) Якщо у задовольняв конгруенцію

у² = х (mod n), (1)

то лишки

y₁ = х mod p, y= mod q (2)

задовольняють конгруенці

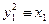(mod p), 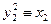(mod q) (3)

Навпаки, якщо у₁ та у₂ задовольняють конгруенції (3), то кожне у, що задовольняє (2), задовольняє також (1).

2) х є квадратичним лишком за модулем п тоді і лише тоді, коли х є квадратичним лишком за кожним iз модулів р і q.

3) Якщо х е квадратичним лишком за модулем п, то конгруенція (1) має в рівно 4 різних розв'язки: у з лишками (y₁, y₂), —у з лишками (p — y₁ ,q — y₂), y^’ лишками (y₁,q — y₂), та -у' з лишками (p-y₁, y_{2 )}

доведення. Пункт 1 випливає безпосередньо із наслідку II.2.13.

Пункт 2 е наслідком пункту 1.

Залишилось обгрунтувати пункт 3. За пунктом 1 конгруенція (1) має стільки ж розв'язків, скільки їх має система (3). Кожна із конгруенцій (3) має рівно 2 взаємно протилежні розв'язки, а відтак саму систему (3) задовольняють рівно 4 різні пари лишків: (y₁ , y₂.), (p — y₁ ,q — y₂), ( y₁ ,q — y₂ ), (p — y₁ , y₂ ).

Як показує твердження 4.1, щоб розв'язати конгруенцію (1) (або розпізнати її розв'язність), досить зробити це для кожної із конгруенцій (3). Тобто, від модуля п = pq ми переходимо до простих модулів р і q. А для простих модулів задачі, що розглядаються, мають ефективні алгоритми, описані у попередніх пунктах. Слід підкреслити, що перехід від модуля п до модулів р і q можливий лише за умови, що ми здатні розкласти число п = pq на співмножники. Таким чином, задачі розпізнавання квадратичності та добування квадратного кореня за модулем n = pq зводяться до факторизації чисел вигляду п = pq.

Зупинимось на цих зведеннях дещо детальніше. Припустимо, що нам відомі обидва дільники р і q модуля п. За пунктом 2 твердження 4.1 число х є квадратичним лишком за модулем п тоді і лише тоді, коли х

є квадратичним лишком за кожним із модулів р і q, що перевіряється якимось із двох способів, згаданих у пункті 4.1.

Для того ж, щоб добути з х квадратний корінь за модулем п, тобто розв'язати конгруенцію (1), можна діяти наступним чином. Слід розв'язати обидві конгруенції (3) за допомогою алгоритму із пункту 4.2, отримавши в результаті y₁ i y₂ Після цього квадратний корінь у визначається з умов (2), як описано у пункті II. 2. 4 (приклад II. 2. 11).

зауваження 4.2. Описане зведення добування кореня за модулем п = pq до факторизації числа п є ймовірнісним, оскільки таким є алгоритм добування коренів y₁ i y₂ за простими модулями р і q. Однак у частковому випадку, коли рq 3 (mod 4) для добування квадратного кореня за модулями р і q є ефективна детермінована процедура (див. випадок 1 алгоритму із пункту 4.2), яка в цьому випадку дає ефективну детерміновану процедуру добування кореня і за модулем п.

приклад 4.3. Обчислимо квадратні корені з х = 58 за модулем п = 77 (р = 7 і q = 11). Спершу обчислюємо х₁ = 58 mod 7 = 2 і х₂ = 58 mod 11 = 3. Використовуємо алгоритм добування коренів за простим модулем з пункту 4.2, причому маємо справу з випадком 1. Знаходимо у₁ =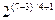mod 7 = 4 і у₂-= 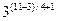mod 11 = 5. За алгоритмом, що міститься в доведенні Китайської теореми про остачі (див. приклад II. 2. 11), отримуємо у = 60. Для пари y₁ i y₂ = (3,5) таким же чином знаходимо ще один корінь у' = 38. Ще два корені 17 і 39 протилежні до вже знайдених.

Виявляється, що й, навпаки, факторизацію чисел вигляду п = pq можна звести до задачі знаходження (хоча б одного) квадратного кореня за модулем п = pq за допомогою ефективної ймовірнісної процедури. Таким чином, задачі добування хоча б одного кореня, знаходження всіх

коренів, і факторизації є попарно еквівалентними відносно поліноміаль-ної ймовірнісної звідності. Зведення, яке ми опишемо, грунтується на такому спостереженні.

твердження 4.4. Нехай у та у' -- два квадратні корені із числа х за модулем п=pq, де р і q різні непарні прості, жодне з яких не ділить х. Припустимо також, що

(mod n) (4)

Тоді НСД (у + у' , п) в одним із дільників р або q числа п.

доведення За умовою маємо у² (у¹)² x (mod n), звідки y² –(y’)²0(mod n)і

(y+y’)(y-y’)0 (mod n). (5)

З умови (4) випливає, що ні у + у', щ у - у' не діляться націло на n. З врахуванням цього, співвідношення (5) дає, що НСД (у + у' ,п) не дорівнює ні 1, ні п. Відтак НСД (у + у', п) дорівнює або р, або q.

Припустімо тепер, що оракул О, отримавши квадратичний лишок за модулем п= qр, видає якийсь квадратний корінь з х за модулем п. Надступний Лас Вегас алгоритм з доступом до оракула О знаходить нетривіальний дільник числа п.

Вхід: п =pq, де р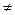q непарні прості.

· Вибрати випадковий елемент у в . Обчислити х = у² mod п

· Зробити оракулу О запит х. Нехай у' = О(х) - відповідь оракула, (y’)² x (mod n)

· Якщо виконується умова (4), то обчислити за допомогою алгоритму Евікліда НСД (у + у’, п) i результат подати на вихід.

Якщо справджується умова (4), то описаний алгоритм згідно із 4.4 справді дає нетривіальний дільник числа п Оскільки y вибирається випадково, то за пунктом 3 твердження 4 1 умова (4) виконується з імовірністю 1/2. Якщо виконувати алгоритм k разів, то ймовірність того, що подія (4) не відбудеться жодного разу, стане 2^-к. зауваження 4.5. Як зазначалось у пункті 1.2, якщо х — квадратичниіі лише за модулем п, то (x/n) ₌ 1, хоча обернене твердження справедливе не завжди. Оскільки символ Якобі легко обчислюється, то задача розпізнавання квадратичних лишків за модулем п = pq еквівалентна такому свому звуженню.

Задано: х, п N, п = pq — добуток непарних простих р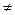q, НСД (х, п) = 1, (x,n) = І.

Розпізнати (чи існує y таке, що ху² (mod n) ?.

Як було показано, ця задача не важча, ніж факторизація модуля n=pq. Однак ніякого ефективного алгоритму на сьогоднішній день для цієєї задачі невідомо.

ВПРАВИ

4.1.а) Довести, що якщо у євипадковим елементом в , де п просте, то х =у² (mod n) є випадковим елементом із Q_n.)

b)Те ж саме для n= pq, де р і q різні прості.

с) Те ж саме для довільного п.

4.2. Чи є квадратичним лишком за модулем 37 число а) 15, ь) 30?

4.3. Знайти якийсь квадратичний нелишок за модулем 83.

4.4. Застосовуючи алгоритм добування квадратного кореня за простим модулем, знайти а) 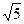(mod 19); b)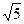mod 29; с) 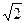mod 41. В останньому пункті використати факт, що 6 є квадратичним нелишком за модулем 29.

4.5. Знайти всі квадратні корені з 60 за модулем 77.

4.6. Нехай п = pq, де р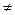q прості. Згідно з пунктом 3 твердження 4.1 кожен квадратичний лишок за модулем п має рівно 4 квадратні корені за цим модулем. Довести, що задача знаходження всіх коренів з числа за заданим одним із них еквівалентна факторизації модуля п відносно ймовірнісної поліноміальної звідності.

4.7. Число п = pq називається цілим Блюма, якщо ріq — різні прості з властивістю рq 3 (mod 4). Розглядаємо звуження задачі розпізнавання квадратичних лишків на множину модулів п, які є цілими Блюма. Припустимо, що існує поліноміальний ймовірнісний алгоритм А, який, отримавши на вхід випадковий елемент х множини J_n = Q_n 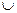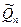, розпізнає, чи х Qn, з ймовірністю щонайменше 1/2 + l/(log n)^c для деякої константи с, де ймовірність визначається як випадковим вибором х, так і випадковою послідовністю алгоритму. Довести, що тоді квадратичні лишки (за модулями, які є цілими Блюма) розпізнаються за поліноміальний час деяким ймовірнісним алгоритмом А'.

ЛІТЕРАТУРА

Опис поліноміального ймовірнісного алгоритму для добування квадратного кореня за простим модулем можна знайти в [111, стор. 47-48], [3, стор. 215-217] або [75]. Першим такий алгоритм опублікував Тонеллі [147]. Ми притримувались викладу цього питання в [13, питання 2 до розділу V].

Звідність факторизації до добування квадратного кореня помічена в [130]. Співвідношення між задачами розпізнавання квадратичності і добування кореня з одного боку, та факторизацією з іншого, переносяться із випадку п = pq на випадок довільного складеного п. При цьому, як і у випадку п = pq, використовується в один бік Китайська теорема про остачі, а в інший - нескладне узагальнення твердження 4.4. Випадок модуля р^α зводиться до випадку простого модуля р (див. [13, §4 розділу V]).

Інші посилання на літературу з цих питань можна знайти в [64].

ЛЕКЦІЯ 15

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Факторизація	\|	Обчислення функції Ойлера

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.