• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Обчислення функції Ойлера

5.1. Випадок аргументу п = pq. Ми почнемо з аналізу задачі

обчислення функції ойлера від п = pq

Задано: п = pq, де р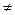q непарні прості.

Обчислити: ф(п).

Слід зазначити, що співмножники р і q не входять в умову задачі. Однак якщо вони, відомі, то ф(п) легко обчислюється за формулою Ф(pq) = (p- 1)(q-1). Таким чином обчислення функції Ойлера від аргументів виду n= pq зводиться до факторизації таких чисел.

Має місце й обернене зведення. Припустимо, що для числа п = pq відоме значення ф(п). Зауважимо, що

ф(п)= п- р- q + 1. Тому співмножники р і q визначаються із системи

тобто є розв'язками квадратного рівняння

X² - Х(п + 1 - ф(п)) + п = 0.

5.2. Деякі узагальнення. Для п = pq позначимо ψ(n) = НСК (р - 1,q- 1). Очевидно, що значення ф(п) є кратним до ψ (п). В попередньому пункті ми бачили, що п легко розкладається на співмножники у випадку, коли відомо значення ф(п). Виявляється, для факторизації числа п досить мати довільне число, кратне ψ (n).

Точніше, факторизація чисел вигляду п = pq, які є добутком двох простих, зводиться за допомогою поліноміального ймовірнісного алгоритму до такої задачі.

Задано: п = pq — добуток двох простих.

Знайти: т таке, що ψ (п) ׀ т і т < .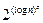

У другій умові на m, c служить позначенням для довільно фіксованої додатної константи. Таким чином, ця умова означає, що довжина запису т повинна обмежуватись деяким поліномом від довжини запису п. Опис зведення, що пропонується нижче, супроводжується коментарями, які допоможуть зрозуміти, чому зведення влаштоване так, а не інакше. При аналізі зведення нам буде зручно на підставі наслідку II.2.13 утотожнювати мультиплікативну групу 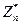з ізоморфною їй групою ×, а елемент х із парою (у, z) ×, де

у = x mod р і z = х mod q. Нагадаємо, що х отримується з (у, z) ефективним чином, як і навпаки.

Перейдемо до опису зведення, тобто деякого алгоритму факторизації чисел п = pq, який має змогу отримувати від оракула певну підказку у вигляді числа m із зазначеними вище властивостями.

Вхід: п = pq, де р 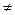q непарні прості.

· Отримати від оракула значення т.

Коментар. Оскільки (р— 1) | і (q — 1) | m, то для кожного хза малою теоремою Ферма

х^т 1 (mod p) і х^т 1 (mod q), звідки

x^m l(mod n). (1)

· Якщо (1) виконується для всіх х, то m має бути парним. Щоб пересвідчитись у цьому, досить взяти х =- 1.

· Зменшити значення т вдвічі.

· Незалежним чином вибрати k випадкових елементів х₁,..., х_k і, використовуючи бінарний метод, піднести їх до степеня т за модулем п.

· Якщо для всіх х =x_і з і k справджується конгруенція (1), то ще раз виконати два попередні пункти. Якщо хоча б в одному випадку (1) порушується, то перейти до наступного пункту.

Коментар. Перед виконанням наступного пункту маємо значення т, для якого (1) виконується не для всіх х . Крім того, з імовірністю щонайменше 1-2^kдля всіх хмаємо

x^2m l(mod n). (2)

(де ймовірність вимірюється за всіма випадковими виборами, що робилися на попередніх кроках, і від яких власне й залежить значення параметру т в поточний момент роботи алгоритму). Справді, множина елементів х, для яких виконується конгруенція (2), утворює підгрупу в . Якщо ця підгрупа власна, то з теореми Лагранжа випливає, що вона містить не більш як половину всіх елементів із . Тому ймовірність того, що всі k випадкових елементів x₁,..., х_k виявились із цієї підгрупи, не перевищує 2^-k.

За допомогою алгоритму Евкліда обчислити значення НСД (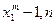),...НСД (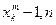) і перше з них, не рівне ні 1, ні п, подати на вихід.

Оцінимо, з якою ймовірністю описаний алгоритм подає на вихід якийсь із нетривіальних дільників р або q числа п. Як зазначалось, із ймовірністю принаймні 1 -2^k для останнього значення параметру m порівняння (2) має місце для всіх х в той час, коли порівняння (1) виконується не для всіх х . Припустимо, що обидва ці факти справді мають місце. Звідси робимо такі висновки. По-перше, m не ділиться на

ф(п)=(р- 1)(q- 1). По-друге, для кожного х степінь х^т є квадратним коренем з1в. Далі розглянемо три випадки.

Випадок 1: (р- 1) | m, (q- 1) | т.

Для х = (y,z) маємо х^т = (у^т,г^т), де піднесення до степеня відбувається в групах , та , відповідно. Для всіх у в маємо за малою теоремою Ферма y^m = 1. Оскільки для всіх х в виконується x^2m=1, то маємо z^2m=1 для всіх z в , зокрема для z, що є твірним елементом групи . Звідси отримуємо, що 2m=d(q-1), для деякого цілого d, i 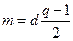. Оскільки хт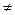1 для деяких х, то z^m =- 1 для деяких z. Тому d повинно бути непарним. Використовуючи критерій Ойлера, отримуємо z^m=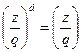для всіх z. Відтак рівно для половини z із маємо z^m = -1, а для іншої половини z^m = -1 (див. пункт ь вправи 1.9). Таким чином, для випадкового х = (y,z) з ймовірністю 1/2 виконується х^т= (1,1), і з такою ж ймовірністю х^т = (1, -1). Іншими словами, завжди х^т 1(mod р), але з ймовірністю 1/2 для випадкового х маємо х^т =- 1 (mod q).

Випадок 2: (q — 1) | m, (р — 1) | т.

Цей випадок симетричний до попереднього. Ті ж міркування показують, що завжди х^т = 1 (mod q), але у половині випадків х^т = -1 (mod p).

Випадок 3: (р — 1) | т, (q — 1)† m.

Такими ж міркуваннями, як у випадку 1, встановлюємо, що для випадкового (у, z) ×степінь (y^m, z^m) з однаковою ймовірністю 1/4 рівний одному з елементів (1,1), (1,-1), (-1,1), (-1,-1). Отже, для випадкового х з ймовірністю 1/2 виконуються конгруенції х^т 1 за одним із модулів р або q та х^т = - 1 за іншим із цих модулів.

Як бачимо, в усіх випадках з імовірністю 1/2 для випадкового х число х^т -1ділиться рівно на одне із чисел р або q, тобто НСД (х^т -1,п) є нетривіальним дільником числа п = pq. Ймовірність того, що цього не трапиться для жодного з k випадкових х₁,.., ,x_k, дорівнює 2^-k.

У підсумку, ймовірність того, що алгоритм не видасть нетривіального дільника числа п, не перевищує 2^-k + 2^-k, де один доданок береться із щойно отриманої оцінки, а другий обмежує ймовірність того, що порушується зроблене на початку наших міркувань припущення про параметр т. Таким чином, алгоритм досягає мети з імовірністю щонайменше 1 -2^-k+1 .

ВПРАВИ

5.1.Число 9991 є добутком двох простих і ф(9991) = 9792. Розкласти його на множники.

5.2.Прослідкувати роботу алгоритму із пункту 5.2 на вході п = 35, припустивши, що оракул робить підказку

т = 48.

ЛІТЕРАТУРА

Зробимо кілька зауважень про зв'язок між задачами обчислення функції Ойлера від довільного аргументу та факторизації. Обчислення ф(п) в загальному випадку зводиться до факторизації аргументу п безпосередньо за формулою для функції Ойлера, встановленою в пункті II.2.4. Існування оберненої звідності доведено за РГР в [45]. У [64] зауважується, що із [45] випливає ймовірнісна звідність факторизації до обчислення функції Ойлера. Зокрема, з [45] виводиться звідність, представлена нами в пункті 5.2 (див. також [111, §2.2 розділу IV]).

Читайте також:

1. Автододавання та автообчислення.
2. Адвокатура в Україні: основні завдання і функції
3. Алг W2 (ОБЧИСЛЕННЯ Y)
4. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
5. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
6. Аналіз коефіцієнтів цільової функції
7. Аналітичні показники динаміки та прийоми їх обчислення
8. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
9. Асимптоти графіка функції
10. База оподаткування, ставки податку та порядок обчислення.
11. Базальні ядра, їх функції, симптоми ураження
12. Базові функції, логічні функції

Переглядів: 969