• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Первісні корені за простим модулем

6.1. Розпізнавання. Тепер розглянемо задачу

Розпізнавання первісного кореня за простим модулем:

Задано: р, g N, де р просте.

Розпізнати: чи g mod р породжує?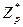

Для цієї задачі невідомо ні детермінованих, ані ймовірнісних поліноміальних алгоритмів. Ситуація змінюється, якщо задано розклад на прості множники числа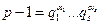. В цьому разі можна застосувати пункт 2 твердження 1.2, згідно з яким g є первісним коренем за модулем р тоді і лише тоді, коли 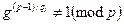для всіх і ≤ s. Останні умови перевіряються ефективно, адже ліва частина легко обчислюється за модулем р за допомогою бінарного методу піднесення до степеня.

Зауважимо, що тим самим встановлено поліноміальну звідність розпізнавання первісного кореня за простим модулем до факторизації.

7.2. Алгоритм Сільвера-Поліга-Гелмана. Для криптоаналізу важливо знати ті часткові випадки, коли дискретне логарифмування можна провести ефективно. Таким є випадок, що p - 1 має лише невеликі прості дільники. Точніше, натуральне число назвемо s-гладким, якщо жоден його простий дільник не перевищує s. У подальшому для модуля р через s будемо позначати найбільший простий дільник числа р - 1. Таким чином, р - 1 є s-гладким. Є алгоритм для знаходження ind(x,g,p), час роботи якого обмежений поліномом від max{s, log p}.

АЛГОРИТМ СІЛЬВЕРА-ПОЛІГА-ГЕЛМАНА

Вхід: х, g, р N, де р просте, р | х, g первісний корінь за модулем р.

Вихід: у = ind(x,g,p).

Робота алгоритму відбувається так. Спочатку факторизуємо число р - 1 безпосереднім діленням його на числа, що не перевищують s. Це займе не більше від s log p операцій ділення. Нехай 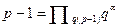- розклад р - 1 на прості множники. Для кожного члена розкладу q ми збираємось знайти лишок у mod q^α. Після того, як це буде зроблено, у легко реконструюється за Китайською теоремою про остачі, точніше, за допомогою алгоритму, що випливає з її доведення.

Отже, розглянемо число q, яке входить у розклад числа р - 1 в степені α. Запишемо

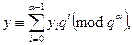де 0 ≤ y_i ≤ q-1

Нашим завданням є визначення послідовності у₀,…,у_α-1 Зауважимо, що

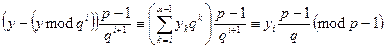
для і = 0, 1,..., α-1. Звідси, з використанням малої теореми Ферма для модуля р і числа g, маємо .

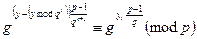
що переписуємо як

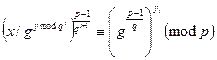(1)

Ділення в основі лівої частини є операцією в

Покажемо, як з останньої конгруенції визначити у_i. При і = 0 отримуємо умову

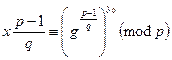(2)

За допомогою бінарного методу піднесення до степеня обчислюємо послідовність чисел

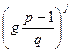для j =0,1,…,q-1 (3)

(яка буде потрібна і для всіх інших і > 0). Зауважимо, що всі елементи послідовності різні, бо g — первісний корінь. Обчислюємо також степінь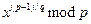, який з огляду на (2) мусить бути рівним одному із членів послідовності (3). Коефіцієнт y₀ дорівнює відповідному показнику j.

Припустимо, що вже знайдено y₀,…,y_i-1 Тоді ми в стані обчислити ліву частину конгруенції (1) за модулем р, оскільки 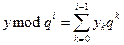Порівнюючи результат з елементами послідовності (3), знаходимо y_i.

Це завершує опис алгоритму.

ВПРАВИ

7.1.а) Довести очікуване для логарифму співвідношення: якщо g і g' —два первісні корені за простим модулем р, і число х не ділиться на р, то ind_gх = ind_gg' ind_g'x.

b) Показати, що логарифмування за всіма можливими основами зводиться до логарифмування за будь-якою одною основою.

7.2. За допомогою алгоритму Сільвера-Поліга-Гелмана обчислити а) ind(11,2,13); ь) ind(25,2,37); c) ind(6,5,97).

ЛІТЕРАТУРА

Огляд відомих алгоритмів дискретного логарифмування зроблено в [64, 114, 111]. Алгоритм Сільвера-Поліга-Гелмана описано в [126] (див. також [111, стор. 98], [42, стор. 17] або [3, стор. 217]).

Поняття логарифму можна розглядати для будь-якої алгебраїчної структури із множенням. Про стан справ із логарифмуванням у скінченних полях дивись [64] і цитовану там літературу. Там же згадане ймовірнісне зведення факторизації до дискретного логарифмування, поширеного на будь-який натуральний модуль. Логарифмування за модулем р^α зводиться до логарифмування за простим модулем р (див. [111, стор. 103]).

Читайте також:

1. В Україні акції можуть бути іменними та на пред'явника, привілейованими і простими.
2. Взаємодія металів з простими та складними речовинами.
3. Відділення коренів
4. Господарська діяльність в первісній історії України
5. Господарська діяльність у первісній історії України
6. Діюче, середнє та середнє за модулем значення струмів і напруг.
7. Історичні корені педагогічної професії.
8. Корені поліномів та їх властивості.
9. Лекція 1. Причини виникнення релігії, її корені. Класифікація релігій
10. Первісні вірування.
11. Первісні музичні інструменти

Переглядів: 1893