Визначники квадратних матриць

Модель оцінки ймовірності банкрутства українських підприємств

Для оцінки ймовірності банкрутства вітчизняних підприємств рекомендується до використання дискримінантна функція із шістьома змінними:

Z = 1,04*X₁+0,75*X₂+0,15*X₃+0,42*X₄+1,8*X₅ -0,06*X₆ - 2,16

Модель розроблена на основі аналізу фінансових показників 850 українських підприємств усіх видів економічної діяльності.

Розшифровка незалежних змінних пропонованої дискримінантної функції наведена в таблиці:

Незалежна змінна	Економічна інтерпретація
Х₁	Коефіцієнт покриття (ліквідність третього ступеня)
Х₂	Коефіцієнт фінансової автономії
Х₃	Коефіцієнт оборотності вкладеного капіталу (активів)
Х₄	Коефіцієнт рентабельності операційних продажів по Cash-flow1
Х₅	Коефіцієнт рентабельності активів по Cash-flow2
Х₆	Коефіцієнт оборотності позичкового капіталу

Використання цієї моделі дозволяє з високим рівнем ймовірності спрогнозувати майбутній фінансовий стан підприємства, а отже, оцінити ймовірність його банкрутства. Точність оцінювання за використання пропонованої моделі є дещо нижчою, ніж у разі застосування відповідних галузевих алгоритмів. Для наведеної дискримінантної моделі рекомендується наступний "ключ інтерпретації" значень інтегрального показника:

· Zi <= -0,55 – фінансовий стан підприємства є незадовільним (знаходиться у фінансовій кризі або вона йому загрожує);

· -0,55 <= Zi <= 0,55 – однозначних висновків щодо якості фінансового стану підприємства зробити неможливо, необхідний додатковий експертний аналіз;

· Zi > 0,55 – фінансовий стан підприємства є задовільним.

У разі, якщо значення показника Zi знаходиться в межах, для яких однозначні висновки щодо якості фінансового стану зробити неможливо, рекомендується додатково застосувати експертні методи аналізу. В рамках чого аналізується динаміка основних абсолютних показників фінансового стану підприємства за два-три роки: валюта балансу; робочий капітал; обсяг виручки від реалізації; величина чистого прибутку (збитку); чистий грошовий потік від операційної діяльності. За результатами додаткового аналізу базовий показник Zi коригується на коефіцієнт (DZ) зміни основних абсолютних показників. Для визначення вагомості впливу окремих абсолютних показників на коефіцієнт коригування можна застосувати загальну методологію дискримінантного аналізу. Скоригований за результатами додаткового експертного аналізу інтегральний показник слід інтерпретувати таким же чином, як це рекомендується вище.

Визначник є числовою характеристикою квадратної матриці, яка використовується при розв’язанні систем лінійних рівнянь, знаходженні обернених матриць тощо. Визначник квадратної матриці А позначається або detA.

Визначником матриці першого порядку називається елемент .

Визначником матриці другого порядку називається число, яке розраховується за формулою .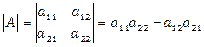

Визначником матриці третього порядку називається число, яке обчислюється за формулою:

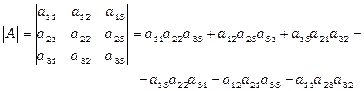За допомогою схеми можна запам’ятати формулу обчислення визначника третього порядку: визначник складається із шести доданків, кожен доданок формули являє собою добуток трьох елементів матриці, вибраних по одному з кожного рядка та кожного стовпчика та позначених на схемі однаковим кольором. Зі знаком «+» беруться три добутки, отримані з лівого малюнку, зі знаком «–» - отримані з правого малюнку. Таке правило обчислення визначників третього порядку називається правилом трикутників.

Приклад 4. Обчислити визначник: .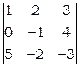

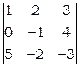=66.

Наведені вище означення визначників є частинними випадками означення визначника n-го порядку. Перед тим, як навести це означення, введемо наступні поняття.

Перестановкою з n елементівназивається впорядкований набір перших n натуральних чисел. Кількість перестановок з n елементів дорівнює .

Два елементи перестановки утворюють інверсію, якщо більший елемент розташований в перестановці перед меншим.

Перестановка називається парною, якщо містить парну кількість інверсій, та непарною, якщо містить непарну кількість інверсій.

Визначником квадратної матриці Аназивається число, що дорівнює сумі всіх можливих добутків елементів матриці А, взятих по одному з кожного її рядка та кожного стовпчика, причому доданок береться із знаком “плюс”, якщо перестановка других індексів елементів, що входять в цей добуток, парна, та із знаком “мінус”, якщо ця перестановка непарна, за умови, що перші індекси цих елементів впорядковані за зростанням. Очевидно, кількість доданків при обчисленні визначника n-го порядку дорівнює n!

Із зростанням розмірності визначника кількість доданків сильно збільшується, тому на практиці при обчисленні визначників вищих порядків загальне означення не використовується. Основним методом обчислення таких визначників є метод пониження порядку.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Модель Беермана	\|	Метод пониження порядку визначника

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.