• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод пониження порядку визначника

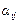Додатковим мінором до елемента квадратної матриціназивається визначник матриці, яка утворюється з даної викресленням того рядка і того стовпчика, де знаходиться цей елемент.

Алгебраїчним доповненням до елемента 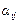квадратної матриціназивається число .

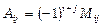Теорема Лапласа.Визначник квадратної матриці дорівнює сумі добутків елементів будь-якого її рядка (стовпчика) на їх алгебраїчні доповнення.

Значення теореми Лапласа полягає в тому, що вона дозволяє звести обчислення визначника n-го порядку до обчислення визначників (n–1)-го порядку.

Приклад 5. Обчислити визначник: .

Розкладемо визначник, користуючись теоремою Лапласа, за першим стовпчиком.

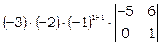== === –30.

Зауваження. З розв’язку видно, що визначник верхньо- або нижньотрикутної матриці дорівнює добутку елементів її головної діагоналі.

Якщо б серед елементів матриці не було б нульових, то використання теореми Лапласа привело б до обчислення чотирьох ненульових доданків з визначниками третього порядку. Отже, в таких випадках перед використанням теореми необхідно спростити елементи визначника, користуючись властивостями визначників.

1.7. Властивості визначників

2. Визначник не змінюється при транспонуванні матриці. Отже, при обчисленні визначника його рядки та стовпчики є рівноправними.

3. Якщо визначник містить нульовий рядок (стовпчик), то він дорівнює нулю.

4. Якщо всі елементи рядка (стовпчика) визначника мають спільний множник, то цей множник можна винести за знак визначника.

5. При перестановці двох довільних рядків (стовпчиків) визначника, визначник змінює знак на протилежний.

6. Якщо визначник містить два однакових рядки (стовпчики), то він дорівнює нулю.

7. Якщо визначник містить два пропорційних рядки (стовпчики), то він дорівнює нулю.

8. Сума добутків елементів одного рядка (стовпчика) визначника на алгебраїчні доповнення до елементів іншого рядка (стовпчика) цього визначника, дорівнює нулю.

9. Визначник добутку матриць дорівнює добутку визначників цих матриць: . З цієї властивості слідує, що хоча 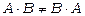, але .

10. Визначник не зміниться, якщо до елементів довільного його рядка (стовпчика) додати відповідні елементи іншого його рядка (стовпчика), помножені на довільне число.

Зауваження. Остання властивість використовується для спрощення елементів визначника перед використанням теореми Лапласа.

Приклад 6. Обчислити визначник: .

Користуючись властивістю 3, винесемо спільний множник з першого стовпчика: =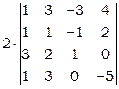. Користуючись властивістю 9, перетворимо визначник так, щоб всі елементи третього стовпчика обертались в нуль, крім одного елементу. Цей елемент називається ведучим. Нехай ведучим елементом, наприклад, буде одиниця, розташована у третьому рядку та третьому стовпчику. Додамо до елементів першого рядка відповідні елементи третього рядка, помножені на 3; до елементів другого рядка додамо відповідні елементи третього рядка. Після цього розкладемо отриманий визначник за третім стовпчиком, користуючись теоремою Лапласа.

==.

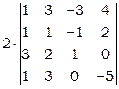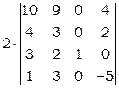Останній визначник можна порахувати за правилом трикутників або продовжити його спрощення. Винесемо спільний множник елементів другого стовпчика за знак визначника та зробимо нульовими елементи цього стовпчика, вибираючи за ведучий його елемент з третього рядка. Після чого розкладемо отриманий визначник за цим стовпчиком.

==

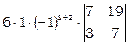===48.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. RLC-фільтр четвертого порядку
6. VII. Нахождение общего решения методом характеристик
7. А. науковий факт, b. гіпотеза, с. метод
8. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
9. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
10. АгротехнІЧНИЙ метод
11. Адаптовані й специфічні методи дослідження у журналістикознавстві
12. Адміністративні (прямі) методи регулювання.

Переглядів: 3729