• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Види матриць

Матрицею-рядкомназивається матриця розмірності .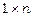

Матрицею-стовпчикомназивається матриця розмірності .

Нульовою називається матриця, всі елементи якої дорівнюють нулю.

Головною діагоналлю матриціназивається множина її елементів з однаковими індексами.

Квадратною матрицеюназивається матриця, яка має однакову кількість рядків та стовпчиків.

Порядком квадратної матриціназивається кількість її рядків (стовпчиків).

Верхньотрикутноюназивається квадратна матриця, всі елементи якої, що знаходяться під головною діагоналлю, дорівнюють нулю.

Нижньотрикутноюназивається квадратна матриця, всі елементи якої, що знаходяться над головною діагоналлю, дорівнюють нулю.

Діагональноюназивається квадратна матриця, у якій ненульовими можуть бути лише елементи головної діагоналі.

Одиничноюназивається діагональна матриця, всі елементи головної діагоналі якої дорівнюють одиниці. Одинична матриця довільного порядку позначається літерою Е.

1.3. Операції над матрицями

Очевидно, що матриця є узагальненням поняття числа (число можна розглядати як матрицю розмірності 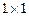), отже для матриць можна визначити операції аналогічні операціям над числами., але деякі з них мають специфічні властивості по відношенню до відповідних операцій над числами.

1. Множення матриці А на число . Добутком матриці А на число називається матриця В=А, елементи якої розраховуються за формулою .

2. Додавання матриць. Сумою двох матриць А та В однакової розмірності називається матриця С=А+В, елементи якої розраховуються за формулою .

3. Транспонування матриць. Транспонованою до матриці А називається матриця , елементи якої розраховуються за формулою .

4. Множення матриць. Операція множення матриці А на матрицю В визначена, якщо кількість стовпчиків першої матриці дорівнює кількості рядків другої матриці, тобто , . За цієї умови добутком матриць А та В називається матриця С розмірності 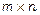, елементи якої розраховуються за формулою .

Приклад 1. Обчислити добуток матриць 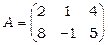та .

Очевидно, що 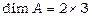, , отже .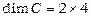

= == =.

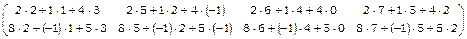Зауваження. Операція множення матриць має специфічні властивості порівняно з операцією множення чисел.

a) З того, що існує добуток 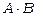, не випливає, що існує добуток . Зокрема, для матриць з прикладу 1 не існує добутку .

b) Якщо навіть добутки 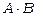та існують, то вони можуть мати різні розмірності. Очевидно, що розмірності цих добутків рівні, якщо А, В є квадратними матрицями однакової розмірності.

c) У випадку, коли добутки 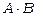та існують та мають однакову розмірність, взагалі кажучи, , тобто порушується комутативний (перестановочний) закон.

Приклад 2. , .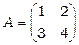

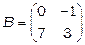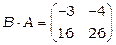, , тобто .

В частинному випадку комутативному закону задовольняє добуток довільної квадратної матриці А на одиничну матрицю відповідної розмірності, тобто 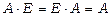. З цього випливає, що одинична матриця при множенні матриць відіграє ту ж роль, що й число 1 при множенні чисел.

d) Добуток двох ненульових матриць може бути нульовою матрицею.

5. Піднесення матриці А до цілого додатного степеня sпозначається та визначається як добуток s матриць рівних А, тобто . Очевидно, ця операція визначена лише для квадратних матриць.

6. Ділення матриць.Введемо цю операцію по аналогії з діленням чисел: частку можна розглядати як добуток числа b на обернене до числа a, тобто , де обернене число 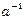визначається із співвідношення .

Оберненою до матриці Аназивається матриця 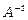, що задовольняє співвідношення , де Е – одинична матриця. Очевидно, що обернену можна визначати лише для квадратних матриць (оскільки інакше розмірності добутків будуть різними).

Оскільки закон комутативності для матричного множення на виконується, то можна визначити два різних ділення матриці B на матрицю A: ділення зліва та ділення справа за умови, що обернена матриця 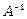існує.

1.4. Елементарні перетворення над матрицями

До елементарних перетворень над матрицями відносяться:

1) перестановки місцями двох рядків (стовпчиків) матриці;

2) множення рядка (стовпчика) матриці на ненульове число;

3) додавання до рядка (стовпчика) матриці іншого її рядка (стовпчика), помноженого на довільне число;

4) викреслення нульового рядка (стовпчика) матриці.

Читайте також:

1. Визначники квадратних матриць
2. Диференціювання та інтегрування матриць.
3. Додавання матриць.
4. Існує багато способів зберігання розріджених матриць.
5. Множення матриць на число.
6. Множення матриць.
7. Операція множення матриць.
8. Подання розріджених матриць
9. Пряма сума квадратних матриць.
10. Транспонування матриць
11. Транспонування матриць.

Переглядів: 2655