• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Транспонування матриць.

Добутки з діагональною матрицею.

D·A =

A·D =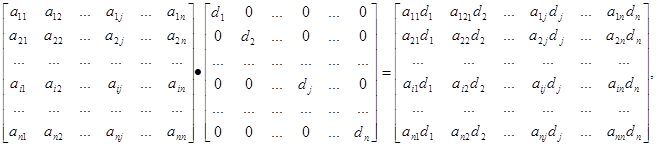

D·K =

=

Діагональна матриця, всі не нульові елементи якої рівні між собою, називається скалярною. Її можна представити як одиничну, помножену на скаляр, тобто

Означення. Транспонування матриці А називається операція заміни рядків цієї матриці її стовпцями із збереженням їхніх номерів.

Матриця, отримана таким чином з матриці А, називається транспонованою відносно матриці А та позначається A^T або A^t.

Отже, нехай задано матрицю А розміром (m ´ n):

.

Переставимо в ній рядки зі стовпцями із збереженням їхніх номерів.

A^t =

Таким чином отримаємо транспоновану матрицю відносно матриці А. Зазначимо, якщо вихідна матриця А має розміри (m ´ n), то транспонована відносно матриці А (А^t) буде мати розміри (n ´ m). У частковому випадку для вектора-рядка транспонованою матрицею буде вектор-стовпець.

Транспонована матриця має такі властивості.

1. Двічі транспонована матриця є вихідною.

A^tt = (A^t)^t = A.

2. Транспонована матриця суми дорівнює сумі транспонованих матриць доданків, тобто

(A + B)^t = A^t + B^t.

3. Транспонована матриця добутку дорівнює добутку транспонованих матриць-співмножників, взятих у зворотному порядку, тобто

(A·B)^t = B^t · A^t.

Читайте також:

1. Диференціювання та інтегрування матриць.
2. Додавання матриць.
3. Існує багато способів зберігання розріджених матриць.
4. Множення матриць.
5. Операція множення матриць.
6. Пряма сума квадратних матриць.
7. Транспонування матриць

Переглядів: 3544