
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Решение
На рис.9.4 построены исходные данные по десяти поездкам.
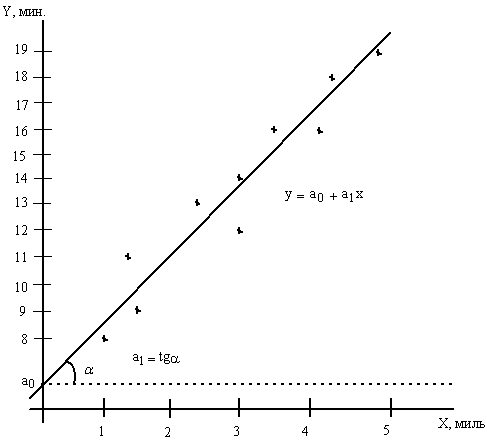
Рис.9.4. График исходных данных задачи №9.01
Помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Построенные точки не находятся точно на линии, что обусловлено описанными выше факторами. Но эти точки собраны вокруг прямой линии, поэтому можно предположить линейную связь между параметрами. Все исходные точки равномерно распределены вдоль предполагаемой прямой линии, что позволяет применить метод наименьших квадратов.
Вычислим суммы, необходимые для расчета коэффициентов линейной регрессии, коэффициента детерминации с помощью табл.9.3.
Таблица 9.3
Вспомогательная таблица задачи №9.01
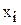
| 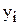
| 
| 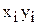
| 
| 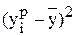
| 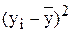
|
| 3,5 | 12,25 | 56,00 | 15,223 | 2,634129 | 5,76 | |
| 2,4 | 5,76 | 31,2 | 12,297 | 1,697809 | 0,36 | |
| 4,9 | 24,01 | 93,1 | 18,947 | 28,59041 | 29,16 | |
| 4,2 | 17,64 | 75,60 | 17,085 | 12,14523 | 19,36 | |
| 3,0 | 9,00 | 36,00 | 13,893 | 0,085849 | 2,56 | |
| 1,3 | 1,69 | 14,30 | 9,371 | 17,88444 | 6,76 | |
| 1,0 | 1,00 | 8,00 | 8,573 | 25,27073 | 31,36 | |
| 3,0 | 9,00 | 42,00 | 13,893 | 0,085849 | 0,16 | |
| 1,5 | 2,25 | 13,50 | 9,903 | 13,66781 | 21,16 | |
| 4,1 | 16,81 | 65,60 | 16,819 | 10,36196 | 5,76 | |
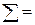 28,9 28,9
| 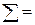 136 136
| 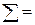 99,41 99,41
| 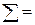 435,30 435,30
| – | 112,4242 | 122,4 |
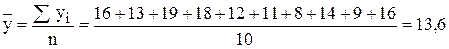 .
.
По формулам (9.3) вычислим коэффициенты линейной регрессии
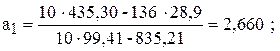
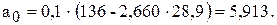
Таким образом, искомая регрессионная зависимость имеет вид

| (9.4) |
Наклон линии регрессии 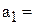 2,66 минут на милю – это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью Y
2,66 минут на милю – это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью Y 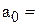 5,913 минут – это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
5,913 минут – это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
По формуле (9.2) вычислим коэффициент детерминации
 или 91,8%.
или 91,8%.
Таким образом, линейная модель объясняет 91,8% вариации времени доставки. Не объясняется 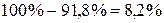 вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
Поскольку коэффициент детерминации имеет достаточно высокое значение и расстояние 2 мили, для которого надо сделать прогноз, находится в пределах диапазона исходных данных (см. табл.9.2), то мы можем использовать полученное уравнение линейной регрессии (9.4) для прогнозирования
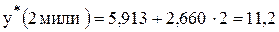 минут.
минут.
При прогнозах на расстояния, не входящие в диапазон исходных данных, нельзя гарантировать справедливость модели (9.4). Это объясняется тем, что связь между временем и расстоянием может изменяться по мере увеличения расстояния. На время дальних перевозок могут влиять новые факторы такие, как использование скоростных шоссе, остановки на отдых, обед и т.п.
Приблизительным, но самым простым и наглядным способом проверки удовлетворительности регрессионной модели является графическое представление отклонений (рис.9.5).

Рис.9.5. График отклонений в задаче №9.01
Отложим отклонения 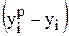 по оси Y, для каждого значения
по оси Y, для каждого значения 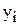 . Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере
. Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере 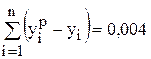 .
.
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Задача №9.01 | | | Нелинейная регрессия |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |