• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Моделі атомних ядер

Спроби побудувати теорію ядра наштовхувалися на труднощі, які були викликані недостатніми знаннями природи ядерних сил, складністю рівняння квантової задачі, тому виникла необхідність йти по шляху створення ядерних моделей. Жодна з існуючих моделей ядра на сьогоднішній день не може повністю описати ядро. Моделей існує дуже багато, і кожна з них описує окремі властивості ядра.

Розглянемо найбільш досконалі з них – краплинну і оболонкову.

1. Краплинну модельядра вперше запропонував Я.І.Френкель у 1936 p., розвинули її Н.Бор і К.Вейцзекер. За цією моделлю ядро уподібнюється краплині рідини. Насправді, подібно до рідини енергія зв'язку і об'єм ядра пропорційні кількості його складових частинок – нуклонів. Подібно до молекул рідини, які взаємодіють з обмеженою кількістю інших молекул, взаємодіям нуклонів властиве насичення. В ядрі, як і в рідині, є поверхневий натяг, зумовлений тим, що поверхневі нуклони взаємодіють з меншою кількістю сусідів, ніж внутрішні. Цей фактор є причиною зменшення енергії зв'язку, яка пропорційна площі поверхні ядра і спостерігається у важких ядрах.

Кількісну основу краплинної моделі ядра становить напівемпірична формула Вейцзекера для повної енергії атомного ядра:

(3.7)

де А – кількість нуклонів; Z – заряд ядра (кількість протонів); a_і, d – константи.

Формулу називають напівемпіричною тому, що в ній тільки перші три члени випливають з краплинної моделі, два останні, а також значення констант знаходять експериментально. Перший член формули показує, що енергія зв'язку ядра пропорційна числу нуклонів; другий, що зменшення енергії зв'язку зумовлюється поверхневим натягом. Ця енергія пропорційна площі поверхні; оскільки радіус ядра R ~ А^1/3, то поверхня 4pR² ~ А^2/3. Третій член визначає зменшення енергії зв'язку, зумовлене силами кулонівського відштовхування. Четвертий член відображує залежність стійкості ядра від співвідношення протонів і нейтронів. Стійкість ядра як системи, за загальною тенденцією, тим більша, чим менша її енергія. Найбільшу стійкість проявляють ядра, в яких кількість протонів і нейтронів однакова N_Р = N_П, або при А = 2Z. Тому відносну кількість протонів і нейтронів виражають 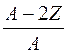. Точний вигляд функції від цього аргументу невідомий. Її вважають незалежною від знака аргументу, тобто від того, що переважає в ядрі, кількість протонів чи нейтронів, тому надають їй квадратичного вигляду. Нарешті, останній член відображує залежність енергії зв'язку від орієнтації спінів нуклонів. Завдяки цьому енергія зв'язку у парно-парних ядер максимальна, а в непарно-непарних – мінімальна. Цей член може набувати додатних і від'ємних значень, що корелюються множником d, а саме:

d = – 1, якщо А – парне, Z – парне;

d = 0, якщо А – непарне;

d = + 1, якщо А – парне, Z – непарне.

Константи a_і мають такі значення в МеВ: a₁ = 15,75; a₂ = 17,8; a₃ = 0,71; a₄ = 23,7; a₅ = 34.

Краплинна модель ядра успішно пояснює основний і збуджений стани ядра. Основний стан ядра, якому відповідає найменша енергія, зображається сфероподібним; збуджений стан – здеформованим (за формою, а не за об'ємом, оскільки йдеться про модель нестисливої краплини). Такі деформації звичайно супроводжуються коливаннями поверхні ядра, отже, відповідні збуджені стани ядра можна характеризувати енергією цих коливань.

Краплинна модель ядра все ж має обмежений зміст. Вона не дає змоги визначити такі важливі характеристики ядра, як спін і магнітний момент.

2. Оболонкова модель.Моделі ядерних оболонок запропонували у 1948 - 1949 pоках М.Гепперт-Майєр та О.Гаксел, І.Ієнсен і Г.Зюсс. Модель передбачає існування в ядрі системи нуклоних оболонок, подібних до електронних в атомах.

Насправді спостерігається аналогія в періодичності властивостей ядер і атомів. Подібно до того, як при відповідних заповненнях електронних оболонок появляються хімічно стійкі атоми – інертні гази, так при певних числах нуклонів спостерігаються особливо стійкі ядра. Експериментально це виявляють у дослідах з бомбардування ядер нейтронами: одні ядра мають більшу ймовірність захоплення нейтрона, інші меншу (ймовірність захоплення інакше називають нейтронним перерізом ядра).

Встановлено, що дуже малі нейтронні перерізи і найбільшу стійкість мають ті ядра, в яких Z a6o (А – Z) дорівнюють так званим магічним числам – 2, 8, 20, 28, 40, 50, 82, 126. Особливо стійкими є двічі магічні ядра: , , , .

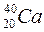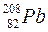Отже, є підстави вважати, що нуклони в ядрі групуються по оболонкам і що магічні числа відповідають до кінця заповненим оболонкам. Оскільки магічні числа належать як до протонів, так і до нейтронів, то напевно вони утворюють окремі системи оболонок; напевно нуклони ядра поступово займають рівні з найменшими енергіями. Формула Вейцзекера дає тільки середнє значення енергії зв'язку, що припадає на нуклон.

Зауважимо, що, як і в електронах, спін нуклонів дорівнює ± 1/2 в одиницях 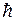, отже, вони підлягають статистиці Фермі - Дірака. Згідно з принципом Паулі, енергії всіх нуклонів ядра повинні бути різними. На енергії нуклона позначається величина його моменту імпульсу.

З погляду оболонкової моделі момент імпульсу нуклона, як і електрона, складається зі спінового і орбітального моментів імпульсу. Величину і напрям останнього визначають за аналогічними умовами квантування.

Можна припустити, що кількість станів нуклона в ядрі дорівнює кількості станів електрона в атомі, а оболонкова модель є копією електронної оболонки. Проте насправді це не так, магічні числа ядер не збігаються з кількістю електронів до кінця заповнених шарів. Ці розбіжності зумовлені особливостями ядерних сил. По-перше, йдеться про сильні взаємодії, з якими важко погодити незалежний рух окремих нуклонів на орбітах; по-друге, в ядрі немає центрального тіла – центра притягання.

Правда, вказані фактори можна спростувати тим, що ядерні сили короткодіючі і тому довжина вільного пробігу нуклона в ядрі може перевищувати радіус ядра. Крім того, ядерні взаємодії нормуються принципом Паулі, який забороняє перехід нуклона з одного стану в інший, якщо всі стани зайняті. Нарешті, для пояснення оболонкової структури ядра можна прийняти, що зовнішні нуклони переміщую­ться у центрально-симетричному полі. Потенціал такого поля можна задати у вигляді:

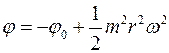. (3.8)

Цю формулу використовували у томсонівській моделі атома, де також немає центрального тіла, але проявляються сили притягання до центра.

Величина j₀ у виразі (3.8) має зміст глибини потенціальної ями в центрі ядра і по суті не накладає обмеження на оболонку, оскільки потенціальна енергія завжди визначається з точністю до довільної сталої. Згідно з цією концепцією, нуклони в середині ядра фактично рухаються вільно, а на поверхні ядра зазнають впливу значних центральних сил притягання і групуються в шарові оболонки.

Крім розглянутих краплинної і оболонкової моделей ядра є ще й інші моделі. Вони свідчать про те, що теорія ядра ще не завершена.

Читайте також:

1. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
2. Алгоритм реалізації моделі
3. Алгоритм реалізації моделі
4. Алгоритм реалізації моделі
5. Алгоритм реалізації моделі
6. Алгоритм реалізації моделі
7. Алгоритм реалізації моделі
8. Алгоритм реалізації моделі
9. Алгоритм реалізації моделі
10. Алгоритм реалізації моделі
11. Аналіз економічноїї політики за допомогою моделі Мандела-Флемінга. Випадки вільного та фіксованого валютного курсів.
12. Аналітичний підбір математичної моделі.

Переглядів: 2916