
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
СОДЕРЖАНИЕ
1. Физические основы механики.. 4
1.1. Основные формулы.. 5
1.2. Примеры решения задач к разделу «Механика». 14
1.3. Базовые задачи для самостоятельного решения. 20
1.4. Контрольные вопросы.. 25
2. Основы молекулярной физики и термодинамики.. 29
2.1. Основные формулы.. 30
2.2. Примеры решения задач к разделу «Молекулярная физика и термодинамика» 35
2.3. Базовые задачи для самостоятельного решения. 38
2.4. Контрольные вопросы.. 43
Библиографический список.. 45
Приложения.. 46
1. Физические основы механики
Физика, наряду с другими естественными науками, изучает объективные свойства окружающего нас материального мира. Физика исследует наиболее общие формы движения материи. Простейшей и наиболее общей формой движения является механическое движение. Механическим движением называется процесс изменения взаимного расположения тел или их частей в пространстве с течением времени.
Классическая механика изучает движение макроскопических тел со скоростями, малыми по сравнению со скоростью света в вакууме. Законы классической механики были сформулированы И. Ньютоном в 1687 году, но не утратили своего значения в наши дни. Движение частиц со скоростями порядка скорости света рассматривается в релятивистской механике, основанной на специальной теории относительности, а движения микрочастиц изучается в квантовой механике. Поэтому законы классической механики имеют определенные границы применения.
Механика включает в себя три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость и ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
В основе классической динамики лежат три закона Ньютона. Здесь необходимо обратить внимание на векторный характер действующих на тела сил, входящих в эти законы.
Динамика охватывает такие вопросы, как закон сохранения импульса, закон сохранения полной механической энергии, работа силы.
При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса.
При изучении раздела «Колебания и волны» следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебаний.
Важно представлять себе, что периодические процессы иной формы, чем гармонические, могут быть представлены в виде суперпозиции гармонических колебаний с различными частотами, амплитудами и начальными фазами.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивление среды, что ведет к диссипации энергии, поэтому колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания, логарифмический декремент и добротность.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы и параметров системы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется механическим резонансом.
При изучении темы "Волны" следует обратить внимание на картину мгновенного распределения смещений и скоростей частиц среды в бегущей волне. Здесь вводится понятие длины волны, скорости распространения волны, волнового числа.
1.1. Основные формулы
Средняя скорость и среднее ускорение:  ;
; 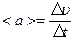 .
. 
где DS – путь, пройденный точкой за интервал времени Dt.
Путь DS в отличие от разности координат Dx = x2 – x1 не может убывать и принимать отрицательные значения, т.е. DS³0.
Величина мгновенной скорости и мгновенного ускорения при прямолинейном движении соответственно:
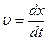 или
или  ;
; 
Тангенциальная и нормальная составляющая ускорения при криволинейном движении:
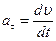 ;
; 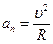 , где R – радиус кривизны траектории.
, где R – радиус кривизны траектории.
Полное ускорение 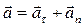 ;
; 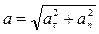
Кинематическое уравнение равнопеременного движения материальной точки (центра масс твердого тела) вдоль оси X:
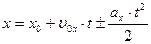 ,
,
где хо – начальная координата движущейся точки в момент времени t = 0;
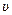 o – скорость точки в данный момент времени;
o – скорость точки в данный момент времени;
а – мгновенное ускорение.
Скорость и путь равнопеременного поступательного движения:
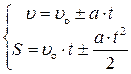 .
.
Угловая скорость и угловое ускорение при вращательном движении:
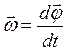 ;
; 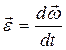 .
.
Кинематические уравнения равнопеременного вращательного движения:
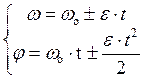
Связь между линейными и угловыми величинами при вращательном движении: длина дуги, пройденная точкой:
 ,
,
где j – угол поворота точки, R – радиус вращения точки;
 ;
; 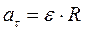 ;
;  .
.
Импульс (количество движения) материальной точки массой m, движущейся со скоростью 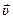 :
:
 .
.
Основное уравнение динамики поступательного движения:
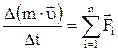 .
.
Силы, рассматриваемые в механике:
а) сила упругости:
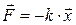 ,
,
где k – коэффициент упругости;
x – абсолютная деформация;
б) сила трения скольжения:
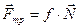 ,
,
где f – коэффициент трения;
N – сила нормального давления;
в) сила гравитационного взаимодействия (сила тяготения):
 ,
,
где G – гравитационная постоянная;
m1 и m2 – массы взаимодействующих тел;
r – расстояние между телами (тела рассматриваются как материальные точки);
г) сила, действующая на тело, движущееся по дуге окружности радиуса R:
 .
.
Закон сохранения импульса (количества движения) для замкнутой (изолированной) системы:
 ,
,
или для двух тел (i = 2):
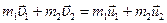 ,
,
где 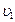 и
и 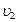 – скорости тел в начальный момент времени (до взаимодействия);
– скорости тел в начальный момент времени (до взаимодействия);
 и
и  – скорости тех же тел после их взаимодействия.
– скорости тех же тел после их взаимодействия.
Кинетическая энергия тела, движущегося поступательно:
 , или
, или  .
.
Потенциальная энергия:
а) упруго деформированного тела:
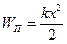 ,
,
где k – коэффициент упругости (жесткость) тела;
x – абсолютная деформация;
б) гравитационного взаимодействия тел:
 ;
;
в) тела, поднятого над поверхностью Земли:
 ,
,
где g – ускорение свободного падения;
h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<RЗ , где RЗ – радиус Земли).
Закон сохранения полной механической энергии (для замкнутой системы, где действуют консервативные силы):
W = Wк+WП = const.
Работа А, совершаемая внешними силами, определяется как мера изменения энергии системы (тела): A = DW = W2 - W1
Работа:
а) постоянной силы F:
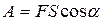 ,
,
где a - угол между направлениями силы  и перемещения
и перемещения  ;
;
б) переменной силы F:
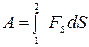
в) упругой силы
 .
.
Мощность:
а) средняя за время Dt
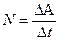 ;
;
б) мгновенная
 , или
, или  .
.
Момент инерции материальной точки
 ,
,
где r – расстояние от точки до оси вращения.
Момент инерции системы (тела):
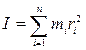 , или
, или  ,
,
где dm – элементарная масса тела;
dV – элементарный объем тела;
r – плотность вещества тела.
Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс (центр симметрии):
а) полого (тонкостенного) и сплошного цилиндров (или диска) радиуса R:
 ;
; 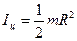 ;
;
б) шара радиуса R:
 ;
;
в) тонкого стержня длиной l, если ось вращения перпендикулярна стержню:
 ;
;
то же, но ось вращения проходит через один из концов стержня:
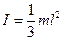 ;
;
г) тела относительно произвольной оси (теорема Штейнера):
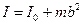 ,
,
где I0 – момент инерции тела относительно оси, параллельной данной и проходящей через его центр инерции;
b – расстояние между параллельными осями.
Момент силы относительно неподвижной точки вращения:
 , или M = F× d,
, или M = F× d,
где  – радиус-вектор точки приложения силы;
– радиус-вектор точки приложения силы;
d – плечо силы F.
Момент импульса материальной точки относительно неподвижной точки:
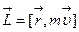 , или
, или 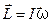 .
.
Основное уравнение динамики вращательного движения твердого тела:
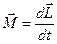 .
.
Проекция на ось Z момента импульса тела, вращающегося относительно неподвижной оси Z:
Lz = Izw, или  ,
,
где w - угловая скорость тела.
Закон сохранения момента импульса (количества движения) для изолированной системы:
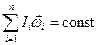 ,
,
где Ii – момент инерции тел относительно оси Zi;
wi – угловая скорость вращения тел системы вокруг оси Z.
Кинетическая энергия вращающегося тела относительно неподвижной оси
 , или
, или 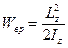 .
.
Работа силы при вращательном движении:
dA = M×dj,
где dj – угол поворота тела.
Кинематическое уравнение гармонических колебаний материальной точки:
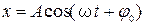 ,
,
где х – смещение колеблющейся точки от положения равновесия;
А – амплитуда колебаний;
w – круговая или циклическая частота;
j0 – начальная фаза колебаний;
t – время.
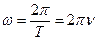 ,
,
где Т – период колебаний точки; v – частота колебаний.
Скорость и ускорение материальной точки, совершающей гармонические колебания согласно уравнения 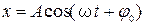 :
:
 –Awsin(wt+j0);
–Awsin(wt+j0);
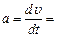 –Aw2cos(wt+j0) = –w2x.
–Aw2cos(wt+j0) = –w2x.
Сила, под действием которой точка массой m совершает гармоническое колебание (возвращающая сила):
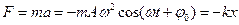 ,
,
где  (m – масса точки).
(m – масса точки).
Кинетическая и потенциальная энергии колеблющейся точки согласно уравнения  :
:
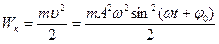 ;
;  .
.
Полная энергия колеблющейся точки:
Е = Wк+WП =  .
.
Период собственных колебаний:
а) математического маятника
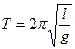 ,
,
где l – длина маятника; g – ускорение свободного падения;
б) пружинного маятника

где m – масса колеблющегося тела; k – жесткость пружины;
в) физического маятника
 ,
,
где I – момент инерции колеблющегося тела относительно оси колебаний;
а – расстояние от центра тяжести маятника до оси колебаний;
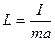 – приведенная длина физического маятника.
– приведенная длина физического маятника.
Уравнение затухающих колебаний (в среде, где сила сопротивления прямо пропорциональна первой степени скорости,  )
)
x = Aoe-β tsin(wt+j1) или x = Aoe-β tcos(wt+j2),
где А – амплитуда в момент времени t = 0; е – основание натурального логарифма; β = 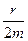 – коэффициент затухания.
– коэффициент затухания.
Логарифмический декремент затухания

где Аt = Aoe-β t– амплитуда в момент времени t.
При сложении гармонических колебаний одного направления с одинаковой частотой (периодом), но разными амплитудами и начальными фазами  ,
,  результирующее колебание описывается уравнением:
результирующее колебание описывается уравнением:
 ,
,
где  – амплитуда результирующего колебания;
– амплитуда результирующего колебания;
 – его начальная фаза.
– его начальная фаза.
При сложении двух взаимно перпендикулярных колебаний одинакового периода, но разных амплитуд и начальных фаз  ,
,  , траектория результирующего колебания задается уравнением:
, траектория результирующего колебания задается уравнением:
 .
.
В зависимости от разности фаз и амплитуд это будет либо прямая, либо эллипс, либо окружность.
Длина волны
 ,
,
где Т – период колебания;
 – скорость распространения волны;
– скорость распространения волны;
v – частота колебаний.
Уравнение плоской бегущей волны:
y = Acosw(t – 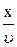 ); у= Acos(wt – kx),
); у= Acos(wt – kx),
где y – смещение любой точки среды, x – расстояние точки от источника колебаний (рис. 1);
 – скорость распространения колебаний в среде;
– скорость распространения колебаний в среде;
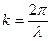 – волновое число;
– волновое число;
 | 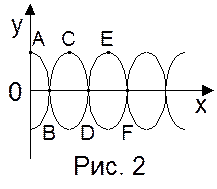 |
l – длина волны.
|
|
 .
.
При падении плоской волны y1 = Asin(wt – kx) на границу раздела двух сред возникает отраженная волна, y2 = Asin(wt + kx) которая, складываясь с падающей волной, образует стоячую волну.
Уравнение стоячей волны у=у1 + у2:
y = 2A cos kx sin wt,
где A(x) = 2A cos kx – амплитуда стоячей волны.
1.2. Примеры решения задач к разделу «Механика»
Пример№ 1. Движение тела массой 2 кг задано уравнением:  , где путь выражен в метрах, время – в секундах. Найти зависимость ускорения от времени. Вычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.
, где путь выражен в метрах, время – в секундах. Найти зависимость ускорения от времени. Вычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.
Дано:

| Решение: Закон изменения мгновенной скорости находим, продифференцировав уравнение движения:
 (1) (1)
|
 – ? – ?
|
Мгновенное ускорение определяется как производная от модуля скорости по времени:
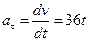 (2)
(2)
Среднее ускорение определяется выражением:
 (3)
(3)
где υ2 – мгновенная скорость в момент времени t2, а  1 – в момент времени t1. Из уравнения (1) находим:
1 – в момент времени t1. Из уравнения (1) находим:  ;
; 
После подстановки:
 (4)
(4)
Равнодействующая сила, действующая на тело, определяется по второму закону Ньютона:
 или
или 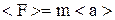
Подставив в эти формулы значения мгновенного и среднего ускорения (формулы (2) и (4)), получим формулы для вычисления искомых значений сил:
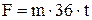 ,
,  (Н)
(Н)
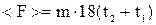 ;
;  (H).
(H).
Ответ: 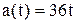 ,
,  ,
,  .
.
Пример№ 2. По наклонной плоскости, составляющей с горизонтом угол 30º, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.
Дано:

| 
|
 - ? - ?
|
Решение: Покажем на рисунке силы, действующие на каждое тело. Запишем для каждого из тел уравнение движения (второй закон Ньютона):
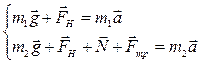
В проекциях на выбранные оси координат:
 на ось (z)
на ось (z)
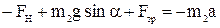 на ось (x)
на ось (x)
 на ось (y)
на ось (y)
Учитывая, что 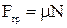 , где
, где  , получим систему уравнений:
, получим систему уравнений:
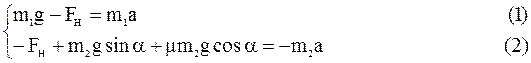
Вычтем из первого уравнения второе:

Отсюда искомое ускорение равно:
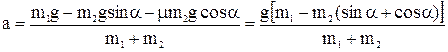
Подставим числовые данные и вычислим значение ускорения а:

Силу натяжения найдем из уравнения (1) системы:
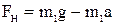 ;
;

Ответ: 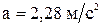 ,
, 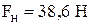 .
.
Пример№ 3. Найти линейные ускорения движения центров тяжести шара и диска, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30º. Начальная скорость тел равна нулю.
Дано:

| 
|
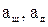 - ? - ?
|
Решение: При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:
 (1)
(1)
где I - момент инерции относительно центра масс тела, m – масса тела; u, ω – соответственно линейная и угловая скорости тел.
Длина наклонной плоскости l связана с высотой соотношением (рис. 1):
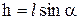 (2)
(2)
Линейная скорость связана с угловой:
 (3)
(3)
После подстановки формул (2) и (3) в формулу (1), получим:
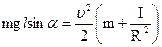 (4)
(4)
Так как движение происходит под действием постоянной силы (силы тяжести), то движение тел – равноускоренное. Начальная скорость 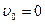 , по условию, поэтому:
, по условию, поэтому:
 (5) и
(5) и 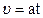 (6)
(6)
Подставляя формулы (5), (6) в формулу (4), получим:
 (7)
(7)
Моменты инерции тел относительно оси, проходящей через центр масс соответственно равны:
| для шара: |  , ,
|
| для диска: | 
|
Подставляя выражение для момента инерции в формулу (7), получим:
| для шара: |  ; ;
|
| для диска: | 
|
Ответ:  ,
, 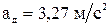 .
.
Пример№ 4. Материальная точка массой 10 г совершает гармоническое колебание с периодом Т=1 с. Определить амплитуду колебаний, максимальную скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.
| Дано: m = 10 г = 10-2кг T = 1 с W = 0,02 Дж | Решение: Уравнение гармонического колебания запишем в виде:  (1), где х - смещение материальной точки из положения равновесия; А - амплитуда; ω - циклическая (круговая) частота; t - время; α - начальная фаза. (1), где х - смещение материальной точки из положения равновесия; А - амплитуда; ω - циклическая (круговая) частота; t - время; α - начальная фаза.
|
A,  max, amax - ? max, amax - ?
|
Скорость колеблющейся точки среды определяется как первая производная от смещения по времени:

Максимальное значение скорости:  . Ускорение точки определяется как производная от скорости по времени:
. Ускорение точки определяется как производная от скорости по времени: 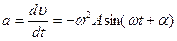 .
.
Максимальное значение ускорения: 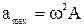 .
.
Полная энергия складывается из кинетической и потенциальной энергии и равна максимальной потенциальной или максимальной кинетической энергии:
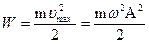
Круговая частота связана с периодом  : . Тогда:
: . Тогда: 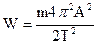
Из этого выражения найдем амплитуду: 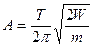 .
.
Проверим размерность:
 .
.
Произведем вычисления:
 ,
,
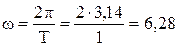 (с-1),
(с-1),
 ,
,

Ответ:  ,
,  ,
,  .
.
Пример№5. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных гармонических колебаний, данных уравнениями: x1 = 0,02cos (5πt + π/2) м и x2 = 0,03cos (5πt + π/4) м. Построить векторную диаграмму сложения амплитуд.
| Дано: x1 = 0,02cos (5πt + π/2) м x2 = 0,03cos (5πt + π/4) м | Решение: Построить векторную диаграмму – это значит представить колебание в виде вектора, длина которого равна амплитуде колебаний, а его угол наклона к оси абсцисс равен начальной фазе колебаний. |
| А, α - ? Дать векторную диаграмму. |
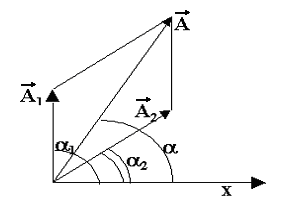 При вращении вектора с угловой скоростью ω проекция его конца на ось будет совершать гармонические колебания.
При вращении вектора с угловой скоростью ω проекция его конца на ось будет совершать гармонические колебания.
Из условия задачи А1=0,02 м = 2 см, α1= π/2, А2=0,03 м = 3 см, α2 = π/4.
Векторная диаграмма изображена на рисунке.
Результирующую амплитуду найдем по теореме косинусов:

Начальная фаза результирующего колебания находится по формуле:

Вычисления: 
 ;
; 
Ответ: А = 4,6 м; α=62о 46′.
Пример№ 6. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания δ = 1,6; начальная фаза равна нулю. Смещение точки в начальный момент времени равно 4,5 см. Написать уравнение колебаний и найти смещение точки в момент времени спустя период Т.
Дано:

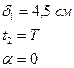
| Решение: Уравнение затухающих колебаний имеет вид:  (1), где β - коэффициент затухания, ω – циклическая частота затухающих колебаний. Найдем ω: (1), где β - коэффициент затухания, ω – циклическая частота затухающих колебаний. Найдем ω: 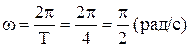 . Логарифмический декремент затухания связан с коэффициентом затухания соотношением: . Логарифмический декремент затухания связан с коэффициентом затухания соотношением:  . Отсюда: . Отсюда:  Подставим ω, β, α в (1) и найдем уравнение затухающих колебаний:
Подставим ω, β, α в (1) и найдем уравнение затухающих колебаний: 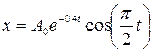 . .
|
 - ? - ?
|
Для начального момента времени при t = 0:
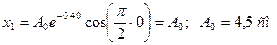
Уравнение колебаний имеет вид: 
Смещение в момент: 

Ответ: 

1.3. Базовые задачи для самостоятельного решения
1. 1. Первую половину времени своего движения автомобиль двигался со скоростью  1 = 80 км/ч, а вторую половину времени – со скоростью
1 = 80 км/ч, а вторую половину времени – со скоростью  2= 40 км/ч. Какова средняя скорость v движения автомобиля?
2= 40 км/ч. Какова средняя скорость v движения автомобиля?
Ответ:  = 60 км/ч.
= 60 км/ч.
2. Тело падает с высоты h= 19,6 м с начальной скоростью  0 = 0. Какой путь пройдет тело за первую и последнюю 0,1 с своего движения?
0 = 0. Какой путь пройдет тело за первую и последнюю 0,1 с своего движения?
Ответ:h1=0,049 м, h2=1,9 м.
3. Зависимость пройденного телом пути s от времени t дается уравнением  , где С = 0,14 м/с2 и D = 0,01m/c3. Через какое время t тело будет иметь ускорение а = 1 м/с2? Найти среднее ускорение а тела за этот промежуток времени.
, где С = 0,14 м/с2 и D = 0,01m/c3. Через какое время t тело будет иметь ускорение а = 1 м/с2? Найти среднее ускорение а тела за этот промежуток времени.
Ответ: t = 12 c; a = 0,64 м/с2.
4. Найти угловую скорость: а) суточного вращения Земли; б) часовой стрелки на часах.
Ответ: а) ω = 72,7∙10-6 рад/с; б) ω = 145,4∙10-6 рад/с.
5. Найти угловую скорость: а) минутной стрелки на часах; б) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин.
Ответ: а) ω = 1,74∙10-6 рад/с; б) ω = 1,19∙10-3 рад/с.
6. Какова линейная скорость  движения искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин., если известно, что его орбита расположена на расстоянии h= 200 км от поверхности Земли?
движения искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин., если известно, что его орбита расположена на расстоянии h= 200 км от поверхности Земли?
Ответ:  = 7,83 км/с.
= 7,83 км/с.
7. Во сколько раз угловая скорость часовой стрелки меньше угловой скорости минутной стрелки?
Ответ: 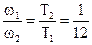 .
.
8. Волчок, вращаясь с частотой 360 об/мин, свободно падает с высоты h = 19,6 м. Сколько оборотов он сделает за время падения?
Ответ:n=12 оборотов.
9. Волчок свободно падает с высоты 4,9 м, вращаясь с периодом 0,02 с. Сколько оборотов сделает волчок за время падения?
Ответ:n=50 оборотов.
10. Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени задается уравнением 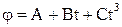 , где В = 2рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую скорость ω; б) линейную скорость
, где В = 2рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловую скорость ω; б) линейную скорость  .
.
Ответ:а) ω = 14 рад/с; б)  = 1,4 м/с.
= 1,4 м/с.
11. Колесо радиусом R = 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени задается уравнением 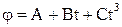 , где В= 2рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловое ускорение ε; б) тангенциальное аτ и нормальное ап ускорения.
, где В= 2рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через время t = 2 с после начала движения: а) угловое ускорение ε; б) тангенциальное аτ и нормальное ап ускорения.
Ответ:а) ε = 12 рад/с2; б) аn = 19,6 м/с2; аτ = 1,2 м/с2.
12. Тело массой 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути s от времени t дается уравнением 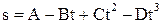 , где С= 5 м/с2 и D = 1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
, где С= 5 м/с2 и D = 1 м/с3. Найти силу F, действующую на тело в конце первой секунды движения.
Ответ:F = 2 H.
13. Молекула массой т = 4,65·10-26 кг, летящая по нормали к стенке сосуда со скоростью  = 600 м/с, ударяется о стенку и упруго отскакивает от нее без потери скорости. Найти импульс силы FΔt, полученный стенкой во время удара.
= 600 м/с, ударяется о стенку и упруго отскакивает от нее без потери скорости. Найти импульс силы FΔt, полученный стенкой во время удара.
Ответ:FΔt = 5,6·10-23 Н∙с.
14. Тело лежит на наклонной плоскости, составляющей с горизонтом угол а = 4. При каком предельном коэффициенте трения μ тело начнет скользить по наклонной плоскости? С каким ускорением а будет скользить тело по плоскости, если коэффициент трения μ = 0,03? Какое время tпотребуется для прохождения при этих условиях пути s = 100 м? Какую скорость u будет иметь тело в конце пути?
Ответ:μ = 0.06993; а = -3,12·10-5 м/с2; t = 22,6 c; u = 8,8 м/с.
15. При подъеме груза массой т = 2 кг на высоту h= 1 м сила F совершает работу А= 78,5 Дж. С каким ускорением а поднимается груз?
Ответ:a = 29,4 м/с2.
16. Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью u0 = 54 км/ч, под действием силы трения Fтр = 6 кН через некоторое время останавливается. Найти работу Асил трения и расстояние s, которое вагон пройдет до остановки.
Ответ:A = –2,25 МДж; s = 375 м.
17. Камень падает с некоторой высоты в течение времени t = 1,43 с. Найти кинетическую Wк и потенциальную Wп энергии камня в средней точке пути. Масса камня т=2 кг.
Ответ:Wк = Wп = 98 Дж.
18. Тело массой m = 2 кг движется навстречу второму телу массой m2 = 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были u1 = 1 м/с и u2 = 2 м/с. Какое время t будут двигаться эти тела после удара, если коэффициент трения μ =0,05?
Ответ:t = 0,58 c.
19. Найти момент инерции Іи момент импульса Lземного шара относительно оси вращения.
Ответ:І = 97,36·1036 кг∙м2; L = 7·1033 кг∙м2 /с
20. Однородный стержень длиной l = 1 м и массой т = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением ε вращается стержень, если на него действует момент сил М= 98,1 мН∙м?
Ответ:ε = 2,35 рад /с2.
21. Однородный диск радиусом R = 0,2 м и массой m = 0,5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости ω вращения диска от времени t дается уравнением  , где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
, где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
Ответ:ε = 2,35 рад /с2.
22.Диск массой m = 2 кг катится без скольжения по горизонтальной плоскости со скоростью u = 4 м/с. Найти кинетическую энергию Wк диска.
Ответ:Wк = 24 Дж.
21. Горизонтальная платформа массой т = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν1=10 об/мин. Человек массой т0 =60 кг стоит при этом на краю платформы. С какой частотой ν2начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека – точечной массой.
Ответ:ν2 = 22 об/мин.
22. Горизонтальная платформа массой т = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ω1= 10 об/мин. Человек массой т0 =60 кг стоит при этом на краю платформы. Какую работу Асовершает человек при переходе от края платформы к ее центру? Радиус платформы R= 1,5 м. Считать платформу однородным диском, а человека — точечной массой.
Ответ:A ≈ 162 Дж.
23. Горизонтальная платформа массой m = 80 кг и радиусом R= 1 м вращается с частотой ν1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой ν2будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от І1 = 2,94 до І2 = 0,98 кг∙м2? Считать платформу однородным диском.
Ответ:ν2 = 21 об/мин.
24. Горизонтальная платформа массой m = 80 кг и радиусом R= 1 м вращается с частотой ω1 = 20 об/мин. В центре стоит человек и держит в расставленных руках гири. Во сколько раз увеличилась кинетическая энергия Wк платформы с человеком, если человек, опустив руки, уменьшит свой момент инерции от І1= 2,94 до І2 = 0,98 кг∙м2? Считать платформу однородным диском.
Ответ:  .
.
25. Однородный стержень длиной l = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальный оси, проходящей через его верхний конец. Найти период колебаний Tстержня.
Ответ:T = 1,16 с.
26. Обруч диаметром D = 56,5 cм висит на гвозде, вбитом в стенку, и совершает малые колебания в плоскости, параллельной стене. Найти период колебаний Тобруча.
Ответ:T = 1,5 с.
27. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится из положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ = 0.
Ответ:t = 2 с.
28. Начальная фаза гармонического колебания φ = 0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?
Ответ: 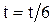 с.
с.
29. Через какое время от начала движения точка, совершающая колебательное движение по уравнению  , проходит путь от положения равновесия до максимального смещения?
, проходит путь от положения равновесия до максимального смещения?
Ответ:t = 1 с.
30.Точка совершает гармоническое колебание. Период колебаний Т= 2 с, амплитуда A = 50 мм, начальная фаза φ = 0. Найти скорость v точки в момент времени, когда смешение точки от положения равновесия х = 25 мм.
Ответ:  = 13,6 см/с.
= 13,6 см/с.
31.Амплитуда гармонических колебаний материальной точки А = 2см, полная энергия колебаний W = 0,3 мкДж. При каком смещении x от положения равновесия на колеблющуюся точку действует сила F= 22,5 мкН?
Ответ:x = 1,5 см.
32. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного шарика алюминиевый такого же радиуса?
Ответ:  .
.
33. Логарифмический декремент затухания математического маятника δ= 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
Ответ: 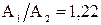 .
.
34. Найти длину волны λ колебания, период которого Т = 10-14 с. Скорость распространения колебаний с = 3∙105 м/с.
Ответ:λ = 3 мкм.
35. Найти смещение x от положения равновесия точки, отстоящей от источника колебаний на расстоянии 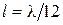 в момент времени
в момент времени 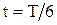 . Амплитуда колебаний А= 0,05 м.
. Амплитуда колебаний А= 0,05 м.
Ответ:x = 2,5 cм.
36. К пружине подвешен груз массой т = 10кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на l = 1,5 см, найти период Твертикальных колебаний груза.
Ответ:T = 0,78 c.
37. Амплитуда гармонических колебаний материальной точки А = 2см, полная энергия колебаний W= 0,3 мкДж. При каком смещении x из положения равновесия на колеблющуюся точку действует сила F= 22,5 мкН?
Ответ:x = 1,5 cм.
38. Найти скорость u течения углекислого газа по трубе, если известно, что за время t = 30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа ρ = 7,5 кг/м3. Диаметр трубы D = 2 см.
Ответ:u = 0,12 м/с.
39. Какое давление Pсоздает компрессор в краскопульте, если струя жидкой краски вылетает из него со скоростью u = 25 м/с? Плотность краски р = 0,8 ∙ 103 кг/м3.
Ответ:P = 250 кПа.
40. Шарик всплывает с постоянной скоростью υ в жидкости, плотность ρ которой в 4раза больше плотности материала шарика. Во сколько раз сила трения Fтр, действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот шарик?
Ответ:  .
.
1.4. Контрольные вопросы
Читайте також:
- Основные направления анализа текста. Методика работы над содержанием прочитанного.
- Предмет и содержание курса «ОХТ»
- СОДЕРЖАНИЕ
- СОДЕРЖАНИЕ
- СОДЕРЖАНИЕ
- Содержание взаимодействия консультанта с клиентом
- Содержание и место самостоятельной работы
- Содержание и особенности маркетингового исследования внешней среды предприятия
- Содержание и форма художественного произведения.
- СОДЕРЖАНИЕ ИТОГОВОГО
- ТЕМА №3. ЗАКОНОМЕРНОСТИ РАЗВИТИЯ ЗЕМЛЕУСТРОЙСТВА. СОДЕРЖАНИЕ ЗЕМЛЕУСТРОЙСТВА-2 ЧАСА
| <== попередня сторінка | | | наступна сторінка ==> |
| К решению задач по физике | | | Элементы кинематики |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |