
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
СОДЕРЖАНИЕ
Авторська редакція
Підписано до друку 5.04.2011. Формат 60×84 1/16. Папір офс. Спосіб друку офс.
Обл.-вид. арк. 9,47. Зам. №298. Наклад 100 прим.
Поліграфічний центр ПолтНТУ
Свідоцтво про реєстрацію ДК № 3130 від 06.03.2000
Лабораторія офсетного друку ПолтНТУ
36011, м. Полтава, просп. Першотравневий, 24
ПолтНТУ
[1] Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде – 12 массой 0.012 кг
* Молярный объем идеального газа при нормальных условиях.
Учебное пособие
К решению задач по физике
Для иностранных студентов
Часть ІI
Полтава – 2011
Навчальний посібник до розв’язання задач з фізики для іноземних студентів. Частина II / Полтава: Полтавський національний технічний університет імені Юрія Кондратюка, 2011. – 63 с. – рос. мовою.
Навчальний посібник призначений для методичного забезпечення аудиторної і самостійної роботи з фізики іноземних студентів інженерно-технічних спеціальностей ПолтНТУ та містить задачі, домашні завдання у вигляді завдань, питання для самоперевірки, перелік завдань до кожного розділу курсу загальної фізики.
Укладачі: Л.О. Черненко, кандидат хімічних наук, доцент кафедри фізики, Р.І. Шматкова, кандидат технічних наук, доцент кафедри фізики
Відповідальний за випуск: завідувач кафедри фізики, д.х.н., проф. В.В. Соловйов
Рецензент: В. П. Якубенко, кандидат фізико-математичних наук, доцент кафедри фізики Полтавського національного технічного університету імені Юрія Кондратюка
Затверджено Вченою радою університету
Протокол № 7 від 30 грудня 2010 р.
Авторська редакція
СОДЕРЖАНИЕ
1. Электричество и магнетизм.. 4
1.1. Основные формулы по электричеству и магнетизму. 4
1.2. Примеры решения задач к разделу «Электричество и магнетизм». 14
1.3. Базовые задачи для самостоятельного решения. 24
1.4. Контрольные вопросы.. 26
2. Оптика.. 30
2.1. Основные формулы.. 31
2.2. Примеры решения задач к разделу «Оптика». 35
2.3. Базовые задачи для самостоятельного решения. 39
2.4. Контрольные вопросы.. 43
3. Квантовая физика.. 45
3.1. Основные понятия и формулы к разделу «Квантовая физика ». 46
3.2. Примеры решения задач к разделу «Физика атома и атомного ядра». 50
3.3. Базовые задачи для самостоятельного решения. 54
3.4. Контрольные вопросы.. 56
Библиографический список.. 58
ПРИЛОЖЕНИЯ.. 59
1. Электричество и магнетизм
Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Силовой характеристикой электрического поля является напряженность 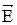 , энергетический - потенциал φ. Следует обратить внимание на связь между
, энергетический - потенциал φ. Следует обратить внимание на связь между 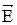 и φ. Для вычисления силы взаимодействия между двумя точечными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона; для вычисления напряженности электрических полей, созданных системой электрических зарядов необходимо применять принцип суперпозиции. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса.
и φ. Для вычисления силы взаимодействия между двумя точечными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона; для вычисления напряженности электрических полей, созданных системой электрических зарядов необходимо применять принцип суперпозиции. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса.
При изучении темы "Постоянный ток" необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца. При изучении "Магнетизма" необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Нужно знать этот закон и уметь применять его для расчета вектора магнитной индукции - основной характеристики магнитного поля. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
При изучении явления электромагнитной индукции необходимо усвоить, что механизм возникновения ЭДС индукции имеет электронный характер. Основной закон электромагнитной индукции - это закон Фарадея-Ленца. Согласно этому закону, ЭДС индукции в замкнутом контуре возникает при изменении магнитного потока, сцепленного с контуром. Необходимо знать, как вычисляется магнитный поток, ЭДС индукции, как рассчитывается работа по перемещению замкнутого контура с током в магнитном поле и энергия магнитного поля.
Электрические и магнитные явления связаны особой формой существования материи - электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
1.1. Основные формулы по электричеству и магнетизму
Закон Кулона: 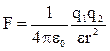 ,
,
где F — сила взаимодействия двух точечных зарядов q1, и q2; r – расстояние между зарядами; e — диэлектрическая проницаемость среды; (для вакуума e = 1); e0 — электрическая постоянная:
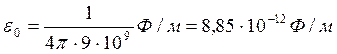 ;
; 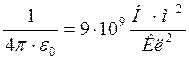 .
.
Напряженность электрического поля в данной точке: E=F/q0, где F — сила, действующая на точечный положительный заряд q0, помещенный в данную точку поля.
Напряженность электрического поля, создаваемого точечным зарядом q0 на расстоянии r от заряда: 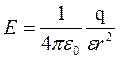 .
.
Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
а) внутри сферы (r<R), E=0;
б) на поверхности сферы (r=R), 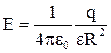 ;
;
в) вне сферы (r>R), 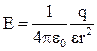 .
.
Принцип суперпозиции электрических полей, согласно которому напряженность 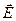 результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:
результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей: 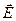 =
= 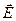 1+
1+ 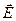 2+...+
2+...+ 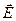 n.
n.
В случае двух электрических полей с напряженностями 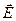 1 и
1 и 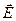 2 модуль вектора напряженности
2 модуль вектора напряженности 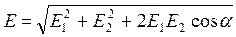 , где a — угол между векторами
, где a — угол между векторами 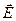 1 и
1 и 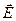 2.
2.
Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянии r от ее оси, 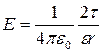 , где
, где 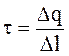 — линейная плотность заряда.
— линейная плотность заряда.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, 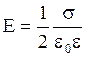 , где
, где 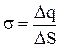 — поверхностная плотность заряда.
— поверхностная плотность заряда.
Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью заряда σ (поле плоского конденсатора)
 .
.
Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенного в данную точку поля, к величине заряда: j=WП/q, или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду: j=A/q.
Потенциал электрического поля в бесконечности условно принят равным нулю.
Отметим, что при перемещении заряда в электрическом поле работа Aв.с внешних сил равна по модулю работе Aс.п сил поля и противоположна ей по знаку: Aв.с= – Aс.п.
Потенциал электрического поля, создаваемый точечным зарядом q0 на расстоянии r от заряда: 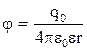 .
.
Потенциал электрического поля, создаваемого металлической, несущей заряд q сферой радиусом R, на расстоянии r от центра сферы:
внутри сферы (r<R): 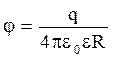 ;
;
на поверхности сферы (r=R): 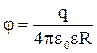 ;
;
вне сферы (r>R):  .
.
Во всех приведенных для потенциала заряженной сферы формулах e –диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, созданного системой п точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраическойсуммепотенциалов j1, j2, ... , jn, создаваемых отдельными точечными зарядами q1, q2, ..., qn: 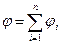 .
.
Энергия W взаимодействия системы точечных зарядов q1, q2, ..., qn определяется работой, которую эта система зарядов может совершить при удаленииих относительно друг друга в бесконечность, и выражается формулой: 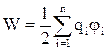 , где ji — потенциал поля, создаваемого всеми n–1 зарядами (за исключением 1-го) в точке, где расположен заряд qi.
, где ji — потенциал поля, создаваемого всеми n–1 зарядами (за исключением 1-го) в точке, где расположен заряд qi.
Потенциал связан с напряженностью электрического поля соотношением:
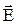 = –gradj.
= –gradj.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой: 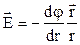 , или в скалярной форме:
, или в скалярной форме: 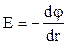 , а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению, E=(j1–j2,)/d, где j1 и j2 — потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
, а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению, E=(j1–j2,)/d, где j1 и j2 — потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал j1, в другую, имеющую потенциал j2, A=q(j1—j2), или 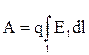 , где El — проекция вектора напряженности
, где El — проекция вектора напряженности  на направление перемещения; dl — перемещение.
на направление перемещения; dl — перемещение.
В случае однородного поля последняя формула принимает вид: A=qElcosa, где l — перемещение; a — угол между направлениями вектора  и перемещения
и перемещения  .
.
Электроемкость:
а) уединенного проводника
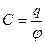 ,
,
где j – потенциал проводника (при условии, что в бесконечности потенциал проводника равен нулю);
б) плоского конденсатора
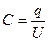 , или
, или 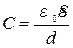 ,
,
где U – разность потенциалов пластин конденсатора;
S – площадь пластины (одной) конденсатора;
d – расстояние между пластинами;
в) уединенной проводящей сферы (шара) радиуса R
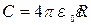 .
.
Электроемкость батареи конденсаторов:
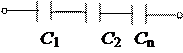 а) при последовательном соединении
а) при последовательном соединении
 ,
,
 б) при параллельном соединении:
б) при параллельном соединении:
С = С1 + С2 + …….+ Сn ,
где n – число конденсаторов в батарее.
Энергия заряженного уединенного проводника
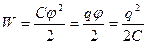 .
.
Энергия заряженного конденсатора
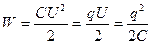 .
.
Объемная плотность энергии электрического поля
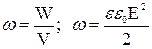 .
.
Сила тока: 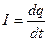 ; для постоянного тока:
; для постоянного тока: 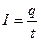 , где dq, q – заряд, прошедший через поперечное сечение проводника за время dt, или t.
, где dq, q – заряд, прошедший через поперечное сечение проводника за время dt, или t.
Плотность тока
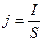 ,
,
где S – площадь поперечного сечения проводника, перпендикулярного току.
Связь плотности тока со средней скоростью  направленного движения заряженных частиц
направленного движения заряженных частиц
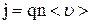 ,
,
где q – заряд частицы; n – концентрация заряженных частиц.
Закон Ома:
а) для однородного участка цепи, не содержащего ЭДС
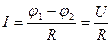 ,
,
где 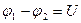 – разность потенциалов (напряжение) на концах однородного участка цепи; R – сопротивление участка;
– разность потенциалов (напряжение) на концах однородного участка цепи; R – сопротивление участка;
б) для участка цепи, содержащего ЭДС
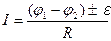 ,
,
где e – ЭДС источника тока на данном участке; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) для замкнутой (полной) цепи
 ,
,
где R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника тока с ЭДС e;
г) в дифференциальной форме
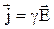 ,
,
где j – плотность тока;
g – удельная проводимость;
Е – напряженность электрического поля.
Сопротивление R и электрическая проводимость s однородного проводника длиной l и площадью поперечного сечения S:
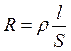 ;
; 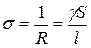 ,
,
где r – удельное сопротивление проводника;
 – удельная электрическая проводимость проводника.
– удельная электрическая проводимость проводника.
Сопротивление проводника с переменным сечением вычисляется путем интегрирования выражения
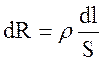 .
.
Общее сопротивление системы проводников:
а) 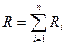 – при последовательном соединении;
– при последовательном соединении;
б) 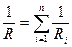 – при параллельном соединении,
– при параллельном соединении,
где Ri – сопротивление i-го проводника.
Законы Кирхгофа:
а) первый закон: 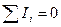 ,
,
где 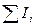 – алгебраическая сумма токов, сходящихся в узле;
– алгебраическая сумма токов, сходящихся в узле;
б) второй закон: 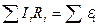 ,
,
где 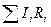 – алгебраическая сумма произведений силы тока на соответствующее сопротивление участка цепи;
– алгебраическая сумма произведений силы тока на соответствующее сопротивление участка цепи;
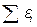 – алгебраическая сумма ЭДС, входящих в рассматриваемый замкнутый контур.
– алгебраическая сумма ЭДС, входящих в рассматриваемый замкнутый контур.
Работа тока:
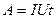 ;
; 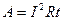 ;
; 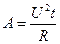 .
.
Мощность тока: 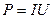 ;
; 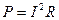 ;
; 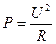 .
.
Закон Джоуля-Ленца (тепловое действие тока в проводнике сопротивлением R за время прохождения тока t)
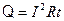 .
.
Полная мощность, выделяющаяся в замкнутой цепи
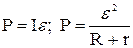 ,
,
где e – ЭДС источника тока.
Закон Био-Савара-Лапласа для элемента проводника с током
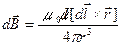 , или
, или 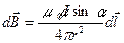 ,
,
где m – магнитная проницаемость изотропной среды;
m0 – магнитная постоянная (m0 = 4p×10-7 Гн/м);
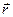 – радиус-вектор, направленный от элемента проводника
– радиус-вектор, направленный от элемента проводника 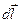 к точке, в которой определяется магнитная индукция
к точке, в которой определяется магнитная индукция 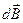 поля;
поля;
α – угол между радиусом-вектором и направлением тока в элементе провода.
Магнитная индукция поля, созданного:
а) бесконечно длинным прямым проводником с током
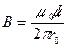 ,
,
где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция;
б) в центре кругового витка с током:
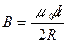 ,
,
где R – радиус витка;
в) отрезком проводника с током:
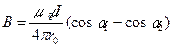 .
.
Обозначения ясны из рисунка.
|
|
|
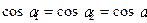 , тогда
, тогда
|
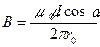 .
.
г) бесконечно длинным соленоидом на его оси (внутри соленоида)

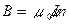 ,
,
где n – отношение числа витков соленоида к его длине.
Связь магнитной индукции 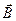 с напряженностью
с напряженностью 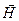 магнитного поля
магнитного поля
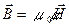 .
.
|
|
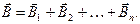
Сила, действующая на прямой провод с током в однородном магнитном поле, называется силой Ампера:
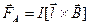 , или
, или 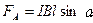 ,
,
где l – длина провода;
α – угол между направлением тока в проводе и вектором магнитной индукции 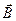 .
.
Если поле неоднородно и провод не является прямым, то:
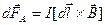
где 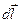 – элемент провода с током I.
– элемент провода с током I.
Магнитный момент плоского контура с током I:
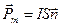 ,
,
где 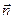 – единичный вектор нормали к плоскости контура, направление которой определяется в соответствии с правилом буравчика;
– единичный вектор нормали к плоскости контура, направление которой определяется в соответствии с правилом буравчика;
S – площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле
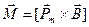 , или
, или 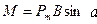 ,
,
где α – угол между векторами 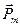 и
и 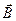 .
.
Сила Лоренца
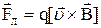 , или
, или 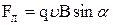 ,
,
где 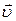 – скорость заряженной частицы; α – угол между векторами
– скорость заряженной частицы; α – угол между векторами 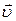 и
и 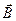 .
.
Если заряженная частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение:
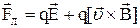 .
.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности
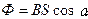 , или
, или 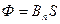 ,
,
где S – площадь контура; α – угол между нормалью 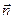 к плоскости контура и вектором магнитной индукции
к плоскости контура и вектором магнитной индукции 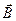 ;
;
б) в случае неоднородного поля и произвольной поверхности:
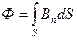 ,
,
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток)
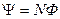 .
.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура с током в магнитном поле
 .
.
Основной закон электромагнитной индукции (закон Фарадея)
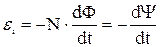 .
.
ЭДС самоиндукции
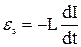 .
.
Индуктивность контура
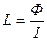 .
.
Индуктивность соленоида, имеющего N витков
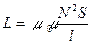 , или
, или 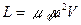 ,
,
где 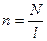 – отношение числа витков соленоида к его длине;
– отношение числа витков соленоида к его длине; 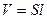 – объем соленоида.
– объем соленоида.
Разность потенциалов на концах провода длиной l, движущегося со скоростью 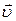 в магнитном поле
в магнитном поле
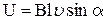 ,
,
где α - угол между векторами 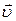 и
и 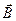 .
.
Заряд, протекающий по замкнутому контуру при изменении магнитного потока ΔΦ, пронизывающего этот контур
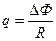 , или
, или  ,
,
где R – сопротивление контура.
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
а) при замыкании цепи
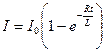 ,
,
где 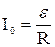 – сила тока в цепи при t = 0;
– сила тока в цепи при t = 0;
t – время, прошедшее после замыкания цепи.
б) при размыкании цепи
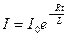 ,
,
где t – время, прошедшее с момента размыкания цепи.
Энергия магнитного поля
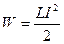 .
.
Объемная плотность энергии магнитного поля
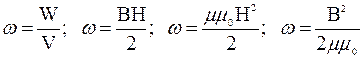 ,
,
где B – магнитная индукция;
H – напряженность магнитного поля;
V – объем магнитного поля.
1.2. Примеры решения задач к разделу «Электричество и магнетизм»
Пример №1. Два одинаковых соприкасающихся шарика подвешены на нитях длиной по 100 см. После сообщения шарикам общего заряда 5  10-7 Кл они разошлись на 100 см друг от друга. Определить массу каждого шарика.
10-7 Кл они разошлись на 100 см друг от друга. Определить массу каждого шарика.
 Дано:
Дано:
l =100см = 1м
q =5  10-7 Kл
10-7 Kл
r = 100 cм = 0,1м
 m-?
m-?
Читайте також:
- Основные направления анализа текста. Методика работы над содержанием прочитанного.
- Предмет и содержание курса «ОХТ»
- СОДЕРЖАНИЕ
- СОДЕРЖАНИЕ
- СОДЕРЖАНИЕ
- Содержание взаимодействия консультанта с клиентом
- Содержание и место самостоятельной работы
- Содержание и особенности маркетингового исследования внешней среды предприятия
- Содержание и форма художественного произведения.
- СОДЕРЖАНИЕ ИТОГОВОГО
- ТЕМА №3. ЗАКОНОМЕРНОСТИ РАЗВИТИЯ ЗЕМЛЕУСТРОЙСТВА. СОДЕРЖАНИЕ ЗЕМЛЕУСТРОЙСТВА-2 ЧАСА
| <== попередня сторінка | | | наступна сторінка ==> |
| Частина І | | | Решение |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |