Четверта позиційна задача

В загальному випадку ця задача формулюється так: визначити проекції точок перетину лінії (кривої або прямої) з поверхнею. Розглянемо алгоритми розв’язання задачі, коли необхідно визначити проекції точок перетину прямих ліній різного положення з поверхнями.

Алгоритм 1- Пряма займає проекціювальне положення.

При такому розташуванні прямої відносно системи площин проекцій одна проекція шуканих точок збігається з виродженою проекцією самої прямої, а дві інші визначають за умови належності поверхні, яку перетинає пряма. Тобто, алгоритм реалізовує принцип одночасної належності шуканих точок двом геометричним фігурам - проекціювальній прямій та поверхні. На рис.6.3 показано циліндричну поверхню і пряму ℓ, яка займає фронтально-проекціювальне положення та перетинає циліндр в точках K і L. Тому фронтальні проекції K2 і L2 шуканих точок перетину лінії ℓ з циліндричною поверхнею збігаються з фронтальною проекцією заданої прямої лінії ℓ2. Горизонтальні проекції K1 і L1 визначені за умови належності точок відповідним твірним циліндра.

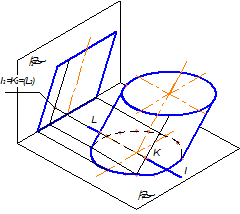
Рисунок 6.3 - Перетин прямої лінії з циліндром

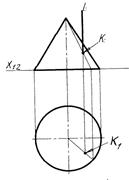
На рис. 6.4 проілюстровано алгоритм визначення проекцій точки перетину прямої ℓ, яка займає горизонтально-проекціювальне положення, з конусом.

Рисунок 6.4 - Перетин прямої лінії з конусом обертання

Алгоритм 2 – Пряма займає загальне положення або положення рівня.

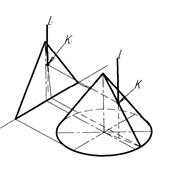
При такому розташуванні прямої лінії визначення проекцій точок її перетину з поверхнею передбачає виконання таких геометричних операцій:

- проведення через пряму допоміжної січної площини (частіше за все – проекціювальної ) – на рис.6.5, а така площина позначена «Т»;

- побудова лінії перерізу поверхні допоміжною площиною – на рис.6.5,б лінія перерізу позначена «а»;

- визначення шуканих точок як точок перетину побудованої лінії перерізу та заданої прямої, на рис. 6.5 такими точками є точки К і L.

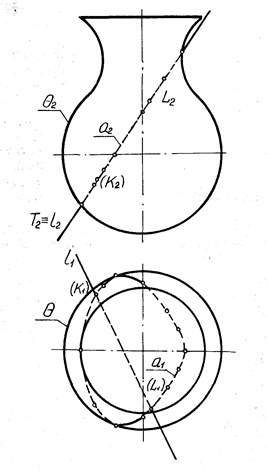
На рис. 6.5,в показано реалізацію наведеного алгоритму для визначення прямокутних проекцій точок перетину лінії загального положення ℓ з поверхнею обертання θ, використовуючи допоміжну січну фронтально-проекціювальну площину Т.

а)

б) в)

Рисунок 6. 5 - Перетин прямої загального положення з поверхнею обертання

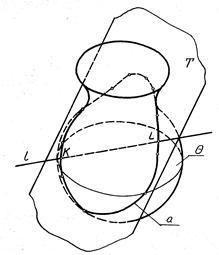
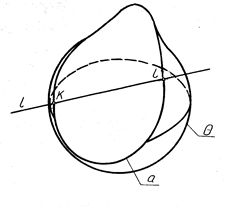
В деяких випадках, особливо для визначення точок перетину прямих з лінійчатими поверхнями, найбільш ефективним є використання допоміжних січних площин - площин загального положення. Доцільність їх використання - отримати переріз поверхні площиною якомога простіший за формою. На рис. 6.6 показано використання допоміжної січної площини загального положення для визначення точок перетину прямої ℓ з еліптичним конусом. Така площина утворена прямими a і ℓ, які перетинаються в точці А, проходить через вершину S і перерізає конус по твірних S1 і S2. Фігуру перерізу знайдено за допомогою попередньо визначеного сліду січної площини на Π1 (пряма MN). Шукані точки K і L є точками перетину побудованого перерізу і заданої прямої.

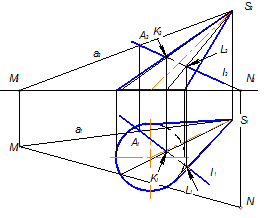
Рисунок 6.6 - Визначення точок перетину прямої з еліптичним конусом

Окремим випадком можна вважати визначення точок перетину прямої з проекціювальним циліндром (циліндром, у якого твірні займають проекціювальне положення), оскільки шукані точки визначають як точки, що одночасно належать циліндричній поверхні та прямій (рис. 6.7 ).

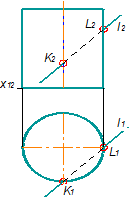
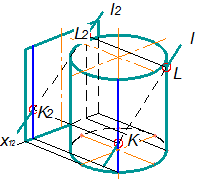
Рисунок 6.7 – Визначення точок перетину прямої з циліндром

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Задача № 58	\|	Задачі для самостійного розв’язування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.