
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Дисконтування при застосуванні механізму простого нарахування процентів
При простому дисконтуванніформула розрахунку приведеної вартості з використанням процентної ставки та при простому механізмі нарахування процентів, має вигляд:
 , (3.1)
позначки PV, FV, і, n мають такі ж значення, що і в формулі (2.2);
де FV – майбутня вартість у грошових одиницях;
PV – початкова вартість у грошових одиницях;
i– процентна ставка у кожному з періодів дисконтування процентівn (у формулі (3.1) процентна ставка i стає показником, що не має розмірності, тобто у формулі показник i використовується не у відсотках, а в частках, в долях, «як темп»);
n – кількість періодів дисконтування процентів впродовж часу (строку) приведення за ставкою і; також, у кожному з цих періодів процентні ставки відповідні періодам та рівні між собою. , (3.1)
позначки PV, FV, і, n мають такі ж значення, що і в формулі (2.2);
де FV – майбутня вартість у грошових одиницях;
PV – початкова вартість у грошових одиницях;
i– процентна ставка у кожному з періодів дисконтування процентівn (у формулі (3.1) процентна ставка i стає показником, що не має розмірності, тобто у формулі показник i використовується не у відсотках, а в частках, в долях, «як темп»);
n – кількість періодів дисконтування процентів впродовж часу (строку) приведення за ставкою і; також, у кожному з цих періодів процентні ставки відповідні періодам та рівні між собою.
|
Дріб 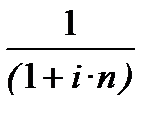 називають дисконтним або дисконтуючим множником (discount factor).
Назвемо його ─ простий дисконтний множник.
Іноді, в літературі, його називають дисконт або коефіцієнт дисконтування.
Цей множник показує, у скільки разів PV менше від FV і є показником, оберненим множнику нарощення. називають дисконтним або дисконтуючим множником (discount factor).
Назвемо його ─ простий дисконтний множник.
Іноді, в літературі, його називають дисконт або коефіцієнт дисконтування.
Цей множник показує, у скільки разів PV менше від FV і є показником, оберненим множнику нарощення.
|
Коли процентні ставки в кожному з періодів нарахування різняться, тобто, якщо процентна ставка змінюється, то формула простого дисконтування приймає вигляд:
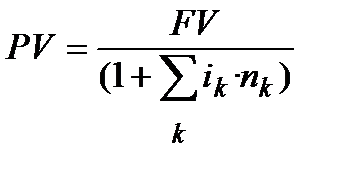 . (3.2)
де і . (3.2)
де і 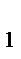 , і , і 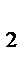 ,…і ,…і  ─ процентні ставки за періоди n ─ процентні ставки за періоди n 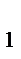 , n , n 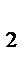 , … …, n , … …, n 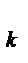 ,відповідно. ,відповідно.
|
Просте дисконтування,яке маєдробову кількість періодів дисконтування (нарахування) процентів.
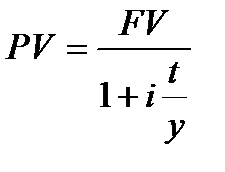 ; (3.3)
де t (time) ─ строк фінансової операції;
у (year) ─ тривалість року, виражена в тих же одиницях, що і t. ; (3.3)
де t (time) ─ строк фінансової операції;
у (year) ─ тривалість року, виражена в тих же одиницях, що і t.
|
Різницю ( 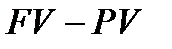 ) можемо розглядати не тільки, як нарощення, не тільки як процент, нарахований на PV, а і як дисконт з суми FV. Показник ─ «дисконт з суми FV» при використанні простої процентної ставки наділимо позначкою ) можемо розглядати не тільки, як нарощення, не тільки як процент, нарахований на PV, а і як дисконт з суми FV. Показник ─ «дисконт з суми FV» при використанні простої процентної ставки наділимо позначкою 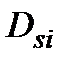 (Discount of simple interest): (Discount of simple interest):
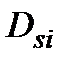 = FV ─ PV = FV ─ = FV ─ PV = FV ─  (3.4) (3.4)
|
Читайте також:
- Адвокатура — неодмінний складовий елемент механізму забезпечення прав людини.
- Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
- Амортизація основних фондів підприємства. Методи нарахування амортизації
- Амортизація основних фондів підприємства. Методи нарахування амортизації.
- Амортизація основних фондів, методи її нарахування.
- Амортизація. Методи нарахування амортизації.
- Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
- Ануїтети з безперервним нарахуванням процентів
- Апарат держави. Орган держави. Інститут держави Апарат держави - частина механізму держави.
- Безперервне нарощення та дисконтування
- Бухгалтерський облік номіналу депозиту та нарахування процентів за депозитом
- Вертикальне наведення.Вертикальне наведення виконується за допомогою прицілу, бічного рівня і підйомного механізму.
| <== попередня сторінка | | | наступна сторінка ==> |
| СТИСЛО ПРО ГОЛОВНЕ В РОЗДІЛІ 3 | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |