
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Безперервне нарощення та дисконтування
Всі нарахування процентів, що розглядалися до цього, мали назву ─ дискретні, тому, що їх нарахування здійснювалося за фіксовані проміжки часу (рік, квартал, місяць, день). Зменшуючи цей проміжок (період нарахування) і, таким чином, збільшуючи частоту нарахування процентів (наприклад m), в результаті можна перейти до так званих безперервних процентів.
Вже згадувалось, що в залежності від частоти нарахування процентів нарощення суми здійснюється змінним темпом, причому, при зростанні частоти нарощена сума (FV) при використанні процентної ставки збільшується. Максимально можливе нарощення здійснюється за умови нескінченного зменшення річного періоду нарахування. Із формули (6.2) при m →+  походить:
походить:
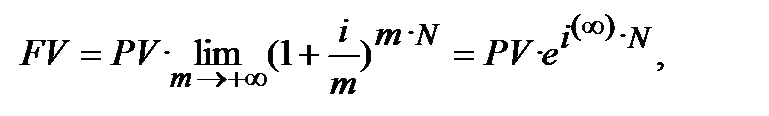 (6.5)
(6.5)
тому, що множник нарощування за номінальною ставкою складних процентів має граничне значення:
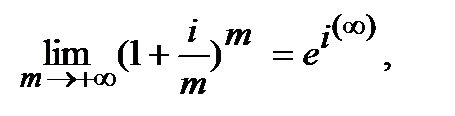 (6.6)
(6.6)
де е ─ ірраціональне число, е = 2,718281… (термін «ірраціональне» означає, що це число точно, без залишку вирахувати не можливо, розрахунок можливий при наперед заданій точності, наприклад, шість знаків після коми…);
е ─ трансцендентне число, тобто не є коренем ніякого алгебраїчного рівняння з цілими коефіцієнтами, його ще називають числом Ейлера;
 ─ безперервна процентна ставка, річна.
─ безперервна процентна ставка, річна.
Щоб відрізняти безперервну ставку від звичайної (дискретної), застосовують особливу позначку безперервної процентної ставки ─ 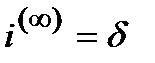 , яка має назву сила росту (force of interest).
, яка має назву сила росту (force of interest).
Сила росту характеризує відносний приріст нарощеної суми за нескінченно малий проміжок часу. Вона може бути незмінною, або змінюватись у часі.
Незмінна сила росту. З урахуванням властивості (6.6) формула (6.2) набуває вигляду:
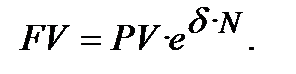 (6.7)
(6.7)
Отже, при безперервному нарощенні процентів нарощена сума (FV) залежить від початкової суми (PV), строку нарощення (N) і сили росту ( 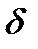 ). Сила росту є номінальною (річною) ставкою складних процентів при m →+
). Сила росту є номінальною (річною) ставкою складних процентів при m →+  , а N ─ кількість років, при чому, N може не бути цілим числом, або може бути цілим числом з дробом.
, а N ─ кількість років, при чому, N може не бути цілим числом, або може бути цілим числом з дробом.
Дискретні складні процентні ставки та безперервні ставки нарощення функціонально залежать одна від одної. Цю взаємозалежність можна вивести із прирівнювання множників нарощення 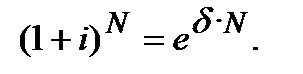 Тоді:
Тоді:
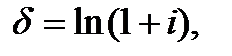 (6.8)
(6.8)
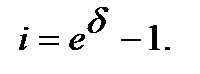 (6.9)
(6.9)
При безперервному складному дисконтуванні із формули (6.4) при m →+  одержуємо:
одержуємо:
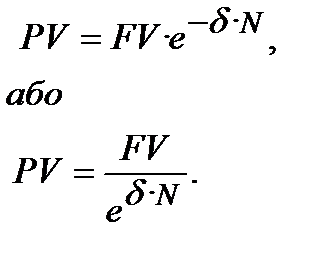 (6.10)
(6.10)
В формулі (6.10)  має назвусила обліку(force of discount) і показує швидкість відносного зменшення суми, що обліковується (все це при механізмі безперервного дисконтування). Формулу (6.10) можемо одержати і з формули (6.7), якщо перетворимо (6.7) відносно PV. Виникає цікавий висновок: сила росту дорівнює силі обліку.В формулах (6.7) та (6.10) множники (коефіцієнти) нарощення ─ це одні і ті ж коефіцієнти кількісно і якісно, тому зникають відмінності між процентним нарощенням і дисконтним обліком при умові безперервного нарощення або дисконтування. І це цілком слушно, тому що в такій ситуації початок періоду та кінець періоду співпадають.
має назвусила обліку(force of discount) і показує швидкість відносного зменшення суми, що обліковується (все це при механізмі безперервного дисконтування). Формулу (6.10) можемо одержати і з формули (6.7), якщо перетворимо (6.7) відносно PV. Виникає цікавий висновок: сила росту дорівнює силі обліку.В формулах (6.7) та (6.10) множники (коефіцієнти) нарощення ─ це одні і ті ж коефіцієнти кількісно і якісно, тому зникають відмінності між процентним нарощенням і дисконтним обліком при умові безперервного нарощення або дисконтування. І це цілком слушно, тому що в такій ситуації початок періоду та кінець періоду співпадають.
Далі, прирівнюючи множники нарощення в формулах (4.5) та (6.10), одержимо зв’язок між силою обліку (силою росту) і річною обліковою ставкою:
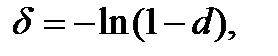 (6.11)
(6.11)
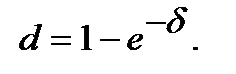 (6.12)
(6.12)
Змінна сила росту.Хай сила росту змінюється у часі відповідно закону, який має вигляд безперервної функції часу: 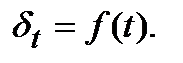 Тоді нарощена сума і теперішня вартість розраховуються так:
Тоді нарощена сума і теперішня вартість розраховуються так:
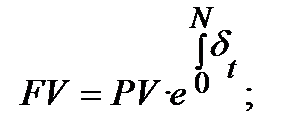

Безперервна функція часу може мати будь-який вид. Розглянемо лише два її варіанти ─ лінійну та експоненціальну.
Лінійна функція:  де ─
де ─ 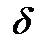 початкове значення сили росту, а ─ приростання сили росту за одиницю часу.
початкове значення сили росту, а ─ приростання сили росту за одиницю часу.
Інтегрування лінійної функції приводить до такого результату:
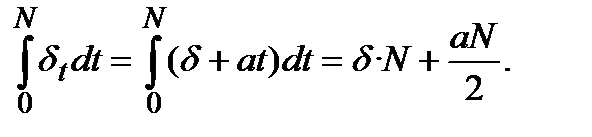
Таким чином, множник нарощення розраховується так: 
_Приклад 6.3___________________________________
Початкове значення сили росту дорівнює 8%, процентна ставка безперервна та лінійно змінюється, приріст за рік складає 2% (а = 0,02). Строк нарощення 5 років. Для розрахунку множника нарощення знайдемо його ступінь:
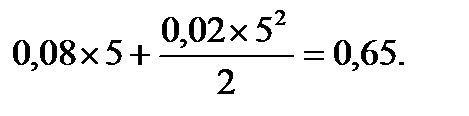
Множник нарощення дорівнює 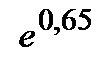 =1,91554.
=1,91554.
У випадку, якщо сила росту лінійно зменшується (наприклад а = ─ 0,02), ступінь множника дорівнює 0,15 і, відповідно,  = 1,16183.
= 1,16183.
Розглянемо варіант, коли сила росту змінюється експоненціально (за геометричною прогресією): 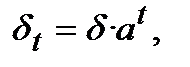
де ─ 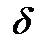 початкове значення сили росту, а ─ постійний темп росту за одиницю часу. В цьому випадку ступінь множника нарощення розраховується так:
початкове значення сили росту, а ─ постійний темп росту за одиницю часу. В цьому випадку ступінь множника нарощення розраховується так:

Отже, множник нарощення розраховується так: 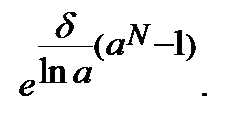
_Приклад 6.4___________________________________
Початковий рівень сили росту дорівнює 8%, процентна ставка безперервно і експоненціально зростає (річний приріст 20%, а = 1,2), строк нарощення 5 років. Необхідно розрахувати множник нарощення.
Ступінь множника нарощення за весь строк дорівнює:
 відповідно
відповідно  =1,92139.
=1,92139.
Розрахунок розміру сили росту.При розрахунку нарощення з незмінною силою росту:
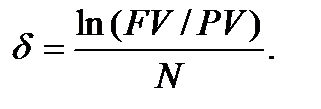 (6.13)
(6.13)
При нарощенні зі змінною силою росту та постійним темпом сили росту а:
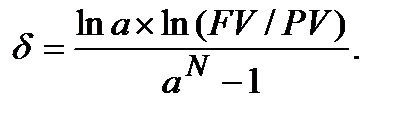 (6.14)
(6.14)
Розрахунок строку позики. Строк позики при незмінній силі росту розраховуємо використовуючи (6.7):
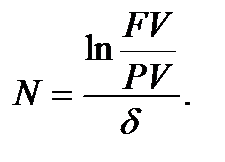 (6.15)
(6.15)
При нарощенні зі змінною силою росту та постійним темпом сили росту а з урахуванням, що множник нарощення дорівнює 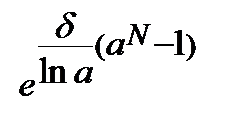 , одержуємо:
, одержуємо:
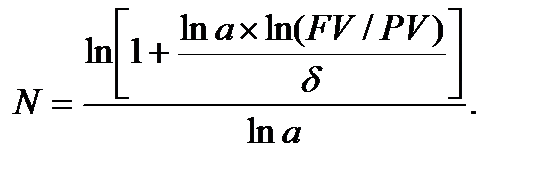 (6.16)
(6.16)
Читайте також:
- Безперервне литво
- Безперервне розливання
- ВИЗНАЧЕННЯ СТАВКИ ДИСКОНТУВАННЯ
- Дисконтування інвестицій, доходів і витрат
- Дисконтування при застосуванні механізму простого нарахування процентів
- Дисконтування при застосуванні механізму простого нарахування процентів
- Дисконтування при застосуванні механізму складного нарахування процентів
- Дохідний підхід: метод дисконтування чистих грошових потоків, метод капіталізації доходу
- Еквівалентність множників утримання та дисконтування для простих процентів
- Еквівалентність множників утримання та дисконтування для складних процентів
- Компаундирування та дисконтування
| <== попередня сторінка | | | наступна сторінка ==> |
| Номінальна процентна та облікова ставки у механізмі простого нарощення та дисконтування процентів. | | | Розрахунки строку позики і розміру ставки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |