• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ідентичність та відмінності основних формул фінансових розрахунків.

Всі формули, що застосовуються у фінансових розрахунках, є похідними всього від чотирьох основних. Саме про ці чотири формули мова йшла в розділах 2,3,4,5. Всі інші формули «виникають» від цих чотирьох, або є їх перетвореними варіантами. Отже, чотири основні формули ─ це формули (2.2), (2.10), (4.1), (4.5), а саме:

1) ─ формула простого нарахування процентів з використанням процентної ставки:

FV = PV·(1+i·n),(2.2)

та похідна від неї формула простого дисконтування з використанням процентної ставки (інша назва ─ формула простої приведеної вартості):

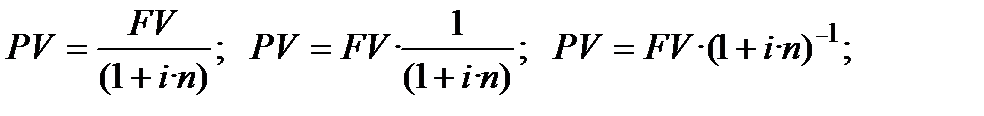(3.1)

2) ─ формула складного нарахування процентів з використанням процентної ставки:

FV = PV ·(1 + і) 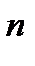, (2.10)

та похідна від неї формула складного дисконтування з використанням процентної ставки (інша назва ─ формула приведеної вартості):

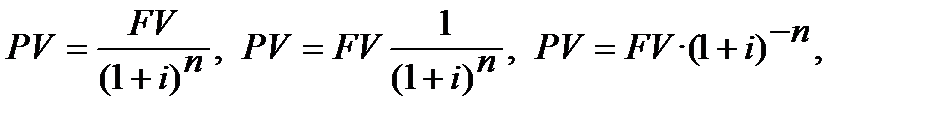(3.6)

3) ─ формула простого дисконтування з використанням облікової ставки:

PV = FV·(1 ─ n·d), (4.1)

та похідна від неї формулапростого нарахування процентів з використанням облікової ставки:

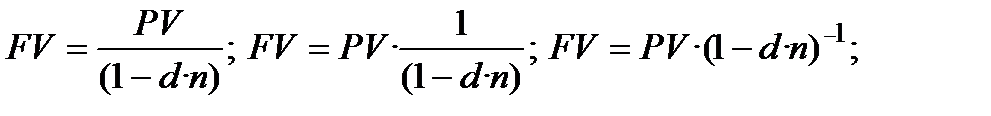(5.1)

4) ─ формула складного дисконтування з використанням облікової ставки:

PV = FV ·(1 ─ d) 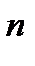, (4.5)

та похідна від неї формуласкладного нарахування процентів з використанням облікової ставки:

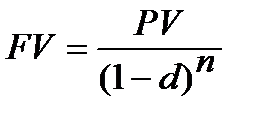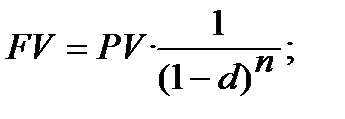
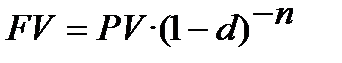; ; (5.6)

Розглядаючи записи формул (2.2), (2.10), (4.1), (4.5) можна побачити, що в них є як спільне так і відмінності.

Спільне:

─ за допомогою кожної з цих чотирьох формул можемо розрахувати або FV, або PV за умов, що інші показники відомі;

─ загалом, в цих чотирьох формулах, показники FV та PV якісно ─ одні і ті ж показники, що показують суму в грошових одиницях на початку фінансової операції ─ PV та суму грошей по її закінченні ─ FV;

─ в кожній з формул є множник у дужках в якому присутня цифра «1».

Відмінності:

─ в кожній з формул множник у дужках відрізняється;

─ саме по множнику у дужках можна визначити, який саме механізм нарахування процентів ─ простий чи складний (якщо дужки мають ступінь ─ це формула складного нарахування процентів, відсутність ступеню, а точніше, ступінь дорівнює одиниці з будь яким знаком «+» чи «-» ─ це формула простого нарахування процентів);

─ також, по множнику у дужках можна визначити, яка ставка процента застосовується ─ процентна ставка чи облікова ставка (якщо в дужках знак «+», то застосовується процентна ставка, якщо в дужках знак «-», то застосовується облікова ставка).

В підрозділі 1.6 (стор. 48) вже йшла мова про необхідність уніфікації позначок, що використовуються в формулах фінансових обчислень, так, як це, наприклад, стало загальноприйнятним в математиці, фізиці, хімії. Але, така уніфікація ─ справа майбутнього. На сьогодні у нас за плечима історія фінансових розрахунків, що налічує майже п’ять сторіч, тому різноманітність позначок, які використовуються ─ реальність сучасних фінансових розрахунків. Щоб розібратися та визначитися з, на перший погляд, «невідомою» формулою треба застосувати для ідентифікації згадані вище спільності та відмінності і знайти відповідну формулу з чотирьох основних не забуваючи, що в кожній з чотирьох основних формул ще існують її можливі похідні варіанти.

_Приклад 6.1___________________________________

«Невідома» формула має таку форму запису: 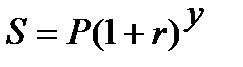. Наявність ступеню «y» для показника в дужках вказує, що механізм нарахування процентів ─ складний. Знак «+» в дужках «інформує», що використовується процентна ставка. З чотирьох зазначених основних формул наведений запис відповідає формулі (2.10) FV = PV ·(1 + і) 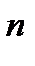, де S ─ це відповідно FV; Р ─ це відповідно РV; r ─ відповідно і, а y ─ відповідно n.

Інший варіант. Формула має такий вигляд: 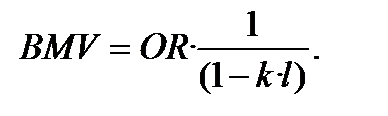Механізм нарахування процентів ─ простий (дужки не мають ступеню, точніше, він є, але дорівнює одиниці). Знак «─» в дужках «показує», що використовується облікова ставка. З чотирьох зазначених основних формул наведений запис відповідає формулі (4.1), а точніше ─ похідній від неї формулі (5.1). Отже, BMV ─ це відповідно FV; OR ─ це відповідно РV; k може бути або n або і, а l ─ відповідно навпаки, або і, або n (відповідність k та l ідентифікувати виходячи з сутності n та і).

Читайте також:

1. IІI. Формулювання мети і завдань уроку. Мотивація учбової діяльності
2. ReM – модифікований критерій Рейнольда, який визначається за формулою
3. Абсолютні й відносні посилання у формулах
4. Амортизація основних засобів
5. Амортизація основних засобів
6. Амортизація основних засобів
7. Амортизація основних засобів і нематеріальних активів.
8. Амортизація основних засобів, основні методи амортизації
9. Амортизація основних засобів.
10. Амортизація основних фондів
11. Амортизація основних фондів
12. Амортизація основних фондів підприємства. Методи нарахування амортизації

Переглядів: 488