• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

У фінансових розрахунках не може йти мова про застосування механізму складного нарахування процентів коли існує тільки дробова кількість періодів нарахування процентів.

Дробова кількість періодів нарахування процентів завжди розраховується за механізмом простого нарахування процентів.» (стор. 101─102).

Доречним є нагадати одне з неоголошених правил.

_____НЕОГОЛОШЕНЕ ПРАВИЛО_(повторно)___

В МЕЖАХ КОЖНОГО ПЕРІОДУ НАРАХУВАННЯ ПРОЦЕНТИ ЗРОСТАЮТЬ ВИКЛЮЧНО ЗА МЕХАНІЗ-МОМ ПРОСТОГО НАРАХУВАННЯ ПРОЦЕНТІВ.

Ствердження, що > при 0 < n < 1, це данина математичним розрахункам, це безпідставне перенесення правил математичних розрахунків в поле фінансових розрахунків. У фінансах на відміну від математичних розрахунків, якщо 0 < n < 1, то множник стає множником, що має дробову кількість періодів нарахування процентів (наприклад, n=t/y) і складний множник в розрахунках «стає простим» .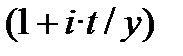

Мабуть автор цього посібника перший хто стверджує: при 0 < n < 1, = . Це певний математичний парадокс, але в практиці фінансових обчислень це ─ дійсність.

В подальших порівняннях процентних множників все за загальноприйнятною схемою.

При n = 1, = .

При n > 1, < .

Порівняємо множники дисконтування, що мають рівні про­сті і складні облікові ставки.

При 0 < n < 1, 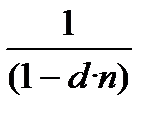= 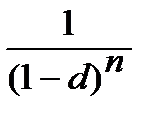. Обґрунтування такого висновку аналогічне обґрунтуванню порівняння при процентних ставках.

При n = 1, = .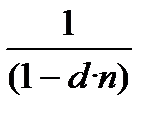

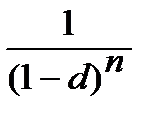При n > 1, > .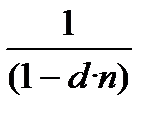

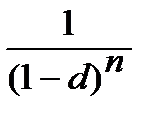Цікавим є порівнювання, коли абсолютні величини процентних і облікових ставок однакові. Виникають такі співвідношення.

При 0 < n < 1, = > = .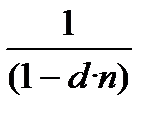

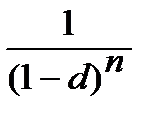При n = 1, 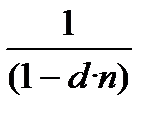= 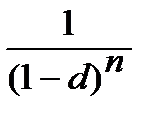> = . (6.32)

При n > 1, > > > .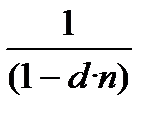

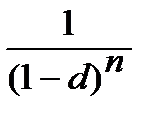Зі співвідношень (6.32) видно, що при 0 < п < 1(тобто на пері­оді, меншому за рік) та при n = 1 (тобто на періоді, рівному року) для дебітора процентні складні і прості, і облікові складні і прості проценти, да­ють однакові результати, але, загалом, облікові вигідніші за процентні.

При n > 1 (тобто на періоді, більшому за рік) найбільш вигідні облікові прості, найменш ─ позичкові прості.

Для кредитора ─ все навпаки.

Можливим є інший варіант порівнювання множників формул (2.2), (2.10), (4.1) ,(4.5), за умови, що формули записані у вигляді PV =FV·k ─ (формули дисконтування).

При 0 < n < 1, = > = .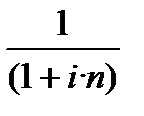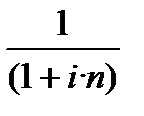

При n = 1, = > = .(6.33) При n > 1, > > > .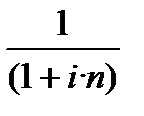

6.6 Розрахунок строку для збільшення початкової суми у k разів (правило 72-х)

Знайдемо в загальному вигляді час (строк, кількість періодів), необхідний для збільшення початкової суми (PV) в k разів при нарахуванні простих і складних процентів. Так, як в обох випадках множники нарощення дорівнюють k, то для механізму простого нарахування процентів використовуючи рівняння 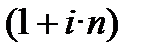= k одержуємо:

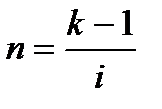, (6.33)

а для складних процентів використовуючи рівняння = k маємо:

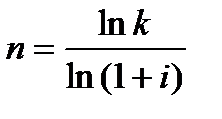. (6.34)

З цих формул можна знайти проміжок часу (період, кількість періодів, кількість років) за який виникає подвоєння початкової суми при процентній ставці і за механізмів простого і складного нарахування процентів. Підставляючи у формули (6.33), (6.34) k = 2, відповідно маємо:

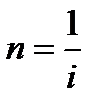(для простих процентів),

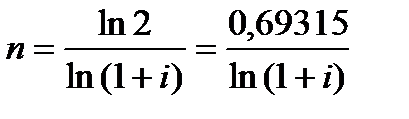(для складних процентів).

В практичних розрахунках для швидкої оцінки ставки нарощення при механізмі складних процентів користуються приблизним розрахунком часу, який необхідно для подвоєння початкової суми, відомим під назвою «правило 72-х». Це правило спрацьовує так: якщо і – процентна ставка, що надана у відсотках, то n = 72/і є кількістю періодів, впродовж яких початкова сума приблизно подвоюється. Це правило досить добре спрацьовує в межах невеликих значень і (і в межах до 20%). Так, якщо річна ставка і = 12%, то n = 6 рокам. Підкреслюємо, що мова йде про кількість періодів нарахування процентів відповідних даному періоду ставки, а саме: якщо базовим періодом, тобто періодом нарощення, наприклад, є половина року, то в розрахунку необхідно використовувати піврічну ставку. Також, треба звернути увагу на таку особливість, незважаючи на те, що в більшості фінансових розрахунків процентна ставка береться десятковим дробом, при застосуванні «правила 72-х» процентну ставку використовують у відсотках.

Існують й інші правила, за допомогою яких швидко розраховують строк подвоєння початкового капіталу при застосуванні конкретної процентної ставки. В літературі можна зустріти «привило 70»: n = 70/і і аналогічне «правило 71». Зазначимо також «правило 69»: n = 69/і + 0,35. Наприклад, при річній ставці і=12% по правилам «70», «71», «69» відповідно одержуємо: n =70/12 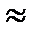5,83 року, n =71/12 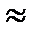5,92 року, n = 69/12+0,35 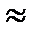6,1 року. Так, як всі перелічені правила дають приблизне значення, то, звичайно, одержуємо розрахунки, результати яких не збігаються. Якщо ж скористатися точною формулою, то одержуємо 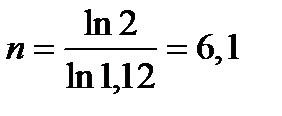року.

В завершення ще раз нагадуємо, що всі згадані «правила» розрахунку строку подвоєння початкової суми «обслуговують» виключно механізм складного нарахування процентів з використанням процентної ставки.

Читайте також:

1. D називається обмеженою зверху (знизу), якщо існує число М
2. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
3. Q6 розраховують тільки при нестаціонарному режимі
4. V. Виконання вправ на застосування узагальнювальних правил.
5. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
6. Абсолютний фагоцитоз або елімінуюча здатність крові (ЕЗК) — це кількість фагоцитованих мікробних клітин лейкоцитами 1 мкл крові.
7. Автомобільні ваги із застосуванням цифрових датчиків
8. Адвокатура — неодмінний складовий елемент механізму забезпечення прав людини.
9. Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
10. Акти застосування норм права в механізмі правового регулювання.
11. Акти застосування юридичних норм: поняття, ознаки, види.
12. Акти правозастосування, їх види

Переглядів: 357