• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Порівняння множників нарощення

Використання у фінансових обчисленнях механізмів простого та складного нарахування процентів дає різні результати, звісно, при умовах порівнювання, тобто, при рівних ставках проценту та однакових строках. Отже, цілком доречним є питання, яка з форм нарахування процентів при рівних став­ках вигідніша з погляду кредитора або дебітора. Для відповіді на це питання знову згадаємо чотири основні формули: (2.2), (2.10), (4.1) ,(4.5).

Будь-яка з цих формул має «свій» множник нарахування (k), якщо їх записати у вигляді FV = PV·k:

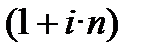─ ─ множник простого нарахування процентів з використанням процентної ставки;

─ ─ множник складного нарахування процентів з використанням процентної ставки;

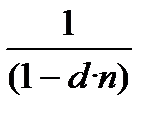─ ─ множник простого нарахування процентів з використанням облікової ставки;

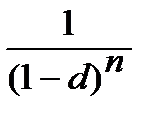─ ─ множник складного нарахування процентів з використанням облікової ставки.

Тому, якщо нарахування здійснюється на рівні суми гро­шей, досить порівняти мультиплікуючі і дисконтуючі множники, тому що саме вони показують, у скільки разів збільшилася (зменшилася) сума за рахунок нарахування про­центів.

Порівняємо множники нарощення, що мають рівні про­сті і складні процентні ставки. Зазначимо, що нарощення по простій процентній ставці відповідає лінійній залежності, а по складній ─ степеневій.

Майже всі джерела, що надають інформацію про порівняння процентних множників нарощення, стверджують, якщо строк фінансової операції менше ніж період нарахування процентів (наприклад, нарахування процентів щорічне, а строк операції ─ менше року, в цьому випадку пишуть 0< n <1), нарощена сума, що розрахована за простими процентами є більшою від нарощеної суми, розрахованої за складними процентами. При доведенні цього ствердження відсилають до розв’язання нерівності, яка завжди, на їхній погляд, є такою: > . Але, на рівні практичних фінансових розрахунків стверджувати, що > при 0< n <1, це, м’яко кажучи, помилка, а, взагалі, це не розуміння суті фінансових розрахунків.

Про помилковість погляду, згідно якого існує на практиці складне нарахування процентів при 0< n < 1, вже говорилося в Додатковій інформації пункту 2.2.2 та у пункті 2.2.3 (стор. 96 ─ 102). Звертаємо увагу на висновки зі згаданих пунктів. «Механізм складного нарахування процентів є механізмом зростання суми з попереднього періоду за наявності наступного, тобто періодів нарахування повинно бути декілька (обов’язково два і більше), тоді і тільки тоді може йти мова про застосування механізму складного нарахування процентів. Але, якщо період нарахування всього один, то зрозуміло, що нема на чому застосовувати механізм складного нарахування процентів. Саме тому, коли період нарахування процентів більший за строк операції, нарахування процентів завжди просте, складному нарахуванню нема на чому застосовувати свій механізм.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Безперервне нарощення та дисконтування
4. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
5. ВПРАВА 2. Утворіть де можливо, форми ступенів порівняння від поданих прикметників.
6. Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
7. Еквівалентність множників нарощування простих та складних процентів
8. Еквівалентність множників нарощування складних процентів за номінальними та ефективними ставками дохідності
9. Еквівалентність множників утримання простих та складних процентів
10. Еквівалентність множників утримання та дисконтування для простих процентів
11. Еквівалентність множників утримання та дисконтування для складних процентів
12. Електроди порівняння в методі потенціометрії

Переглядів: 408