• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.

8. Ми вже розглянули три числових множини: натуральні, цілі та раціональні числа. У кожній із цих множин ми навчилися порівнювати та виконувати арифметичні операції додавання, віднімання, множення і ділення. При порівнянні чисел виявилося, що натуральні і цілі числа набагато простіше порівнювати, ніж дробові. Разом з тим, досить легко порівнювати дробові числа з однаковими знаменниками. Саме ця ідея й була використана для запису дробових чисел без знаменника, що значно спрощувало порівняння таких чисел. Розглянемо систему числення з основою q. У такій системі числення довільне натуральне число nєN можна записати як суму добутків цифр цієї системи на степені основи системи числення наступним чином: n=a_kq^k+a_k-1q^k-1+a_k-2q^k-2+…+a₂q²+a₁q¹ +a₀q⁰, де nєN і a_k, a_k-1, a_k-2,…, a₂, a₁, a₀ – цифри числа n у системі числення з основою q. Інколи таке число записують і так: n=a_ka_k-1a_k-2…a₂a₁a₀. При таких записах порівнювати та виконувати арифметичні операції набагато простіше, бо існують відповідні алгоритми.

Видатний узбецький математик і астроном аль-Коші продовжив такий запис на числа менші за одиницю, відділивши більші за одиницю та менші за одиницю числа комою. Завдяки цьому він отримав такі записи: 1) r=a_kq^k+a_k-1q^k-1+a_k-2q^k-2+…+a₂q²+a₁q¹+…+a₀q⁰+b₁q^-1+b₂q^-2+b₃q^-3+…+b_mq^-m, де a_k, a_k-1, a_k-2, …, a₂, a₁, a₀, b₁, b₂, b₃,…,b_m – цифри числа r у системі числення з основою q; 2) r=a_ka_k-1a_k-2…a₂a₁a₀b₁b₂b₃…b_m. Такі дробові числа прийнято називати системними або систематичними дробами.

Означення: системним або систематичним дробом називають дріб, чисельник якого записано у деякій позиційній системі числення з основою q, а знаменник дорівнює степені основи q.

Якщо q=10, ми приходимо до поняття десяткових дробів, наприклад: 864,23=8•10²+6•10¹+4•10⁰+2•10^-1+3•10^-2=86423/10². Отже, приймаємо таке означення та без доведення кілька теорем.

Означення: десятковим дробом називається звичайний дріб із знаменником, що дорівнює степені десяти, записаний в десятковій позиційній системі числення

Означення: цифри, що стоять у десятковому дробі після коми, називаються десятковими знаками.

Теорема 1: множення десяткового дробу на 10ⁿ досягається перенесенням коми на n знаків (цифр) вправо.

Теорема 2: ділення десяткового дробу на 10ⁿ досягається перенесенням коми на n цифр вліво.

Теорема 3: дописування або відкидання у десятковому дробі нулів, які стоять наприкінці десяткового дробу, не змінює його величини.

Теорема 4: для зведення десяткових дробів до спільного знаменника достатньо приписати до того десяткового дробу, в якого менше десяткових знаків, стільки нулів, щоб десяткових знаків в обох дробах стало порівну.

На основі цієї теореми можна вважати, що всі десяткові дроби зведені до спільного знаменника.

Означення: число, яке стоїть у десятковому дробові до коми, називається цілою частиною. Число, яке стоїть у десятковому дробові після коми, називається дробовою частиною.

Теорема 5: із двох десяткових дробів більшим є той, у якого ціла частина більша. Із двох десяткових дробів з рівними цілими частинами більшим є той, у якого більший перший з нерівних десяткових знаків.

Для того, щоб виконувати операції над десятковими дробами, спочатку розглянемо питання про можливість перетворення звичайних дробів у десяткові та десяткових у звичайні. З шкільного курсу математики відомо, що легко перетворити будь-який десятковий дріб у звичайний, а от не всякий звичайний дріб можна перетворити у десятковий. Для перетворення десяткового дробу в звичайний його записують із знаменником, який є степенем числа 10, а потім, по можливості, проводять скорочення звичайного дробу до нескоротного. Відповідь про можливість перетворення звичайного дробу у десятковий дає наступна теорема.

Теорема 6: для того, щоб нескоротний дріб 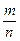можна було записати у вигляді десяткового дробу, необхідно і достатньо, щоб до канонічного розкладу знаменника входили лише прості множники 2 і 5.

Читайте також:

1. Автоматичний обмін даними.
2. Адаптивні хвилькові перетворення : Хвилькові пакети.
3. Активні операції банків
4. Активні операції комерційних банків
5. Алгебраїчні операції
6. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
7. Анімізм – уявлення про існування духовних істот та віра в можливість спілкування з ними.
8. Арифметичні операції
9. Арифметичні операції в різних системах числення
10. Арифметичні операції над цілими числами
11. Банк і його операції. Правова природа банківської діяльності
12. Бартерні операції

Переглядів: 1646