Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

При механізмі складного нарахування процентів.

Нагадуємо, що основна формула розрахунку майбутньої вартості при механізмі складного нарахування процентів ─ FV = PV ·(1 + і) 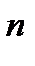, (2.10). Ця формула не враховує інфляційні зміни. Тому, спочатку розглянемо варіанти, ─ а) ─ е)(див. далі по тексту), в яких проведемо розрахунки майбутньої вартості грошей з урахуванням повної компенсації інфляційного зростання цін, потім, після узагальнення, вийдемо на запис формули, яка вміщує в собі «інфляційну складову».

а) Строк фінансової операції ─ 1 рік, нарахування процентів ─ річне (n = 1), і ─ номінальна ставка, рівень інфляції за цей же рік ─ inf %, тоді сума грошей через рік без врахування інфляції Сума грошей через рік, яка б компенсувала інфляційне знецінення грошей, тобто така FV, яка є збільшеною на суму інфляційних втрат, розраховується в даному випадку так: 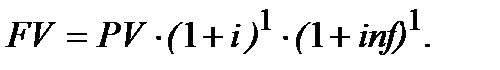Майбутню вартість, яка враховує інфляцію так, що зберігає такі ж купівельні можливості для грошей сумою 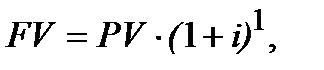як і для грошей PV, і тому збільшену на індекс інфляції 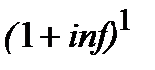будемо позначати FVii (від англ. inflationery increase, а можливо і від addition) (інфляційне збільшення, інфляційна добавка). Отже, FVii ─ майбутня вартість з інфляційною добавкою.

б) Строк ─ 1 рік, нарахування процентів ─ річне (n = 1), і ─ номінальна ставка, рівень інфляції за цей же рік надано як середньомісячний за рік ─ 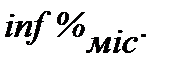Тоді: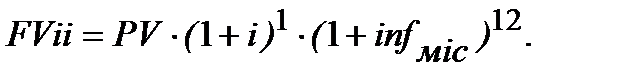

в) Строк ─ 1 рік, нарахування процентів ─ річне (n = 1), і ─ номінальна ставка, рівень інфляції за цей же рік надано окремо за кожний місяць ─ 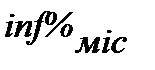і всі місячні показники різні. Тоді:

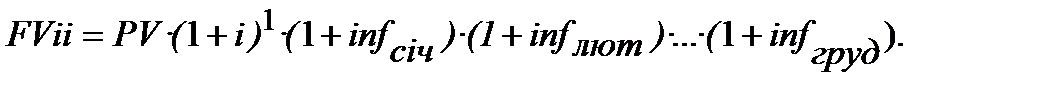
г) Строк фінансової операції ─ три роки, нарахування процентів ─ річне (отже, n = 3), і ─ номінальна ставка, рівні інфляції в кожному з трьох років ─ 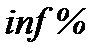(річні, можливо середньорічні та однакові для кожного року). Тоді: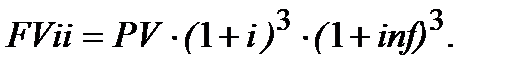

Якщо рівень інфляції за ці три роки надано як середньомісячний в кожному з трьох років ─ 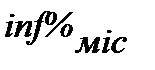. Тоді,

Якщо рівні інфляції за ці три роки надано як річні (середньорічні) в кожному з трьох років ─ 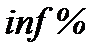і всі річні показники різні, тоді: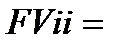

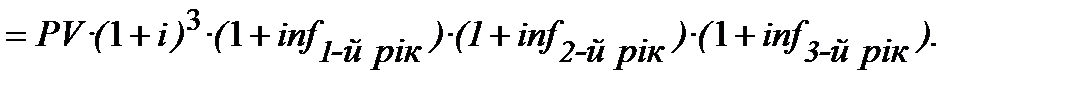д) Строк фінансової операції ─ три роки і сім місяців, нарахування процентів ─ щорічне (тоді, n = ), і ─ номінальна ставка, рівні інфляції в кожному з трьох років ─ 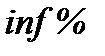(річні, середньорічні) і однакові. В цьому випадку використовуємо формулу змішаного нарахування процентів (2.15) і одержуємо:

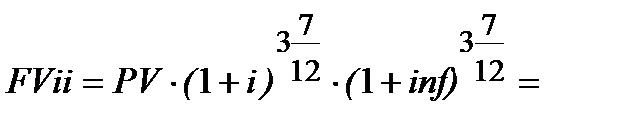
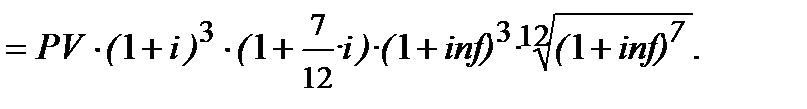
Нагадуємо, що пояснення, чому 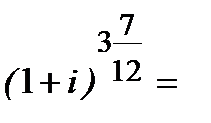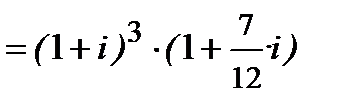─ надано в пункті 2.2.2, де мова йде про складне нарахування процентів, якщо є ціла і дробова кількість періодів нарахування процентів (так зване змішане нарахування процентів). Звертаємо увагу, що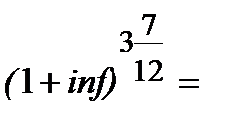 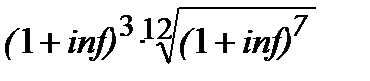ґрунтується на (10.10).

е) Строк фінансової операції ─ три роки (N = 3), нарахування процентів ─ щомісячне, тобто m = 12, (тоді, n = N·m), номінальна ставка і, рівні інфляції в кожному з трьох років ─ (середньорічні, однакові). В такому випадку використовуємо формулу (6.2) і одержуємо:

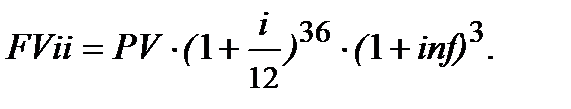
Якщо рівень інфляції за ці три роки надано як середньомісячний в кожному з трьох років ─ 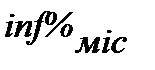, тоді:

В практичних розрахунках можливі і інші варіації нарахувань процентів з врахуванням інфляційної добавки за яких обчислюється майбутня вартість. Майбутню вартість, яка враховує інфляцію таким чином, що зберігає такі ж купівельні можливості для грошей майбутньої суми як і для грошей PV, тому, що збільшує показник 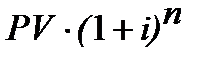на індекс інфляції 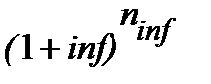, як вже згадувалося, будемо позначати ─ FVii. Назви і позначки FVii можуть відрізнятися в учбових і наукових джерелах. Наприклад, у Бланка [2, стор. 171] цей показник позначається 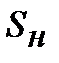і має таку характеристику: «…номінальна майбутня вартість вкладу (грошових коштів), що враховує фактор інфляції». В наших розрахунках FVii будемо в основному іменувати: майбутня вартість з інфляційною добавкою, майбутня вартість з інфляційною компенсацією, майбутня вартість з інфляційним збільшенням або …з інфляційним нарощенням, майбутня вартість з урахуванням компенсації інфляційного зростання цін. Така прискіплива увага до трактування FVii викликана тим, що існує ще однин показник майбутньої вартості з врахуванням фактору інфляції (про це в пункті 10.2.2).

Але, повертаємось до визначення запису загальної формули розрахунку FVii, ─ формули майбутньої вартості грошових коштів з урахуванням повної компенсації інфляційного зростання цін. На підставі узагальнення розрахунків у варіантах а)─е)можемо записати:

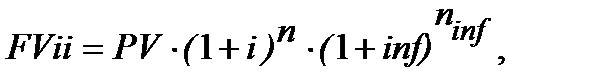(10.14)

де FVіі – майбутня вартість з урахуванням компенсації інфляційного зростання цін;

PV – початкова вартість у грошових одиницях;

i– процентна ставка у кожному з періодів нарахування процентів n ;

n – кількість періодів нарахування процентів впродовж часу (строку Т) застосування ставки і; також, у кожному з цих n періодів процентні ставки рівні між собою;

inf ─ темп інфляції у кожному з періодів 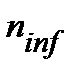за проміжок часу (строку Т) застосування ставки і;

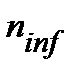─ кількість періодів інфляції, в кожному з яких темпи інфляції рівні між собою та дорівнюють inf і які в сумі дорівнюють або не перевищують строк Т;

Т ─ строк фінансової операції.

Звертаємо увагу, що у формулі (10.14) показники n і 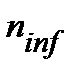можуть співпадати чисельно, а можуть бути різними. Це пов’язано з тим, що кожний з показників «працює на свою ставку», є показником кількості «своїх» періодів, і тому їх кількість може не співпадати. Те, що дає їм можливість спільно працювати в одній формулі, є обов’язкове виконання вимоги: кількість 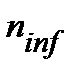сумарно дорівнює або не перевищує загального строку фінансової операції (Т) в межах якого функціонує кількість n.

Формула (10.14) може бути записаною в такій редакції:

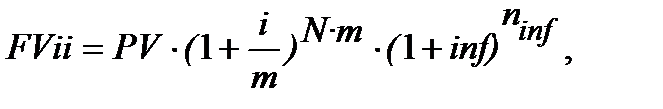(10.15)

де i– номінальна (річна) процентна ставка;

m ─ кількість періодів нарахування процентів у році;

N ─ кількість років впродовж строку;

inf ─ темп інфляції у кожному з періодів 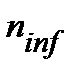за проміжок часу, строку Т, строку, який дорівнює або не перевищує N·m;

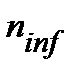─ кількість періодів інфляції, в кожному з яких темпи інфляції рівні між собою та дорівнюють inf і які в сумі дорівнюють або не перевищують строк Т=N·m.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Застосування показників інфляційного знецінення грошей у фінансових розрахунках.	\|	При механізмі простого нарахування процентів.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.