• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вічний ануїтет

Вічний ануїтет, безстроковий ануїтет, або ─ перпетуітет (від англ. ─ perpetuity) ─ це ряд платежів, кількість яких не обмежено у часі. Теоретично ─ це виплати, (вклади) впродовж безкінечного у часі строку. В практиці фінансів існують випадки, коли строки ануїтетів не оговорено, мається на увазі, що вони дуже великі і тому вважається, що строк не має кінця, а виплати (вклади) здійснюються безкінечно, або ─ вічно. Прикладами можуть бути виплати процентів по деякім видам облігацій або виплати дивідендів по привілейованим акціям.

Цілком правильним є твердження, що (FV) нарощена сума вічного ануїтету є безкінечно великою величиною, а теперішня вартість вічного ануїтету є конкретною величиною, яка розраховується вельми просто.

Якщо брати формулу 12.5:

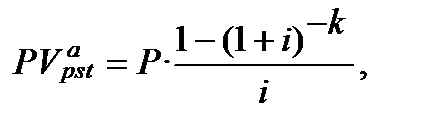(12.5)

в якій k → 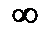, то теперішня вартість вічного ануїтету розраховується:

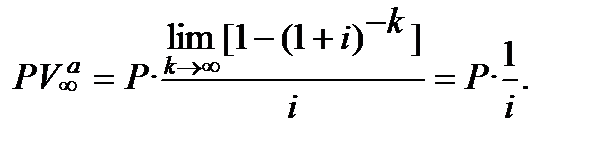(12.35)

Отже, формула розрахунку теперішньої вартості вічного ануїтету має такий вигляд:

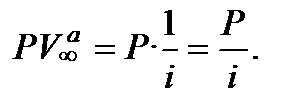(12.36)

У формулі (12.36) є дві суттєві особливості.

Перша, ─ ця формула використовуються тільки тоді, коли період нарахування процентів співпадає з періодом внесення платежів. Іншими словами, ─ якщо платежі раз в рік і нарахування річне; якщо платежі кожного півріччя і нарахування процентів по півріччям; якщо платежі щоквартальні і нарахування процентів щоквартальне, загалом ─ коли m = p, то тільки в цих випадках формула (12.36) дає правильний результат.

Друга особливість, ─ показник і є показником процентної ставки в кожному з періодів нарахування, тобто, в цій формулі і ─ не завжди річна ставка, це ставка в кожному з періодів m.

Якщо внесення платежів раз на рік з m-разовим нарахуванням процентів в році, тобто при p = 1, m > 1, то формула розрахунку теперішньої вартості вічного ануїтету має розраховується за формулою:

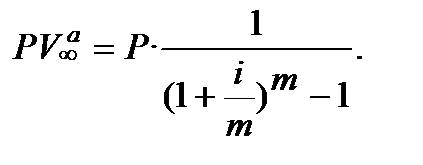(12.37)

У випадку внесення платежів р-раз за рік з нарахуванням процентів один раз на рік (тобто, при p > 1, m = 1)

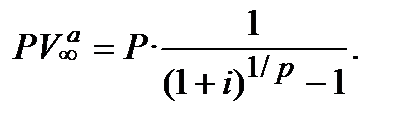(12.38)

При внесення платежів р-раз на рік з m-разовим нарахуванням процентів в році (при p >1, m >1, за умови що ):

(12.39)

Якщо в формулах 12.37, 12.38, 12.39 ─ p = 1 та m = 1, то ці формули перетворюються у формулу 12.36.

Читайте також:

1. Ануїтети з безперервним нарахуванням процентів
2. Ануїтети з виплатами в середині періодів
3. Відкладений ануїтет
4. Змішані ануїтети
5. Кількість теплоти. Перший закон термодинаміки. Вічний двигун першого роду
6. Лекція 11 Тимчасова, майбутня і теперішня вартості грошей, дисконтування, ануїтет в аналітично - управлінському моделюванні прийняття рішень
7. Майбутня та теперішня вартості авансового ануїтету (ануїтету пренумерандо)
8. Майбутня та теперішня вартості авансового ануїтету (ануїтету пренумерандо) при використанні облікової ставки
9. Майбутня та теперішня вартості звичайного ануїтету (ануїтету постнумерандо)
10. Майбутня та теперішня вартості звичайного ануїтету (ануїтету постнумерандо) при використанні облікової ставки
11. При розрахунку показників грошових потоків виводимо та користуємося формулами виключно тільки для ануїтетів.

Переглядів: 1208