• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язування задачі

Використовуємо формулу (12.45)

(12.45)

за якою проводимо розрахунок строку ануїтету.

Перед застосуванням формули (12.45) треба з’ясувати, чи може забезпечити щомісячне погашення боргу в розмірі 2000 грн накопичення суми 130 тис. грн з процентами. Для формули (12.45) необхідне додержання такої нерівності: P >

Розрахунок коефіцієнта у квадратних дужках дає такий результат: 0,025954834658. Тоді Р повинно бути більше ніж 3374 грн. Тобто, платіж в 2000 грн не забезпечить накопичення суми 130 тис. грн з процентами ні при якому строку виплат. Це означає, що виплата у 2000 грн не «перекриває» навіть суму процентів за перший місяць, а якщо це так, то сума боргу буде постійно щомісячно зростати.

Необхідно змінити розмір щомісячної виплати, який повинен бути більшим за 3374 грн. Новий узгоджений з покупцем розмір щомісячної виплати хай дорівнює 3500 грн. За нових умов строк, за який буде погашено кредит, розраховується за формулою (12.45) та дорівнює:

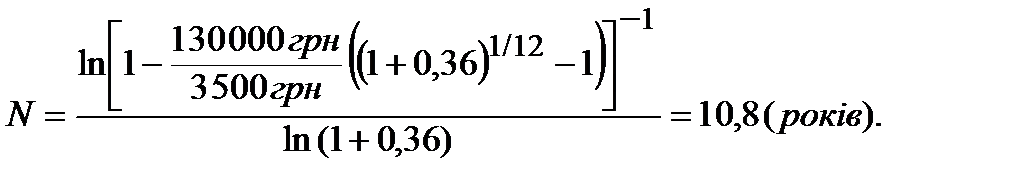Строк 10,8 років є строком між 10 роками і 9-ма місяцями та 10 роками і 10-ма місяцями, а точніше ─ це 10 років та 292 дні, або 10 років 9 місяців і 22 дні. У відповідності до зауважень, що надані у розділі 12 після формули (12.53), округлюємо строк до показника 10 років та 9 місяців, що відповідає показнику 10,75 років.

Виконаємо розрахунок з використанням округленого показника N=10,75 років за формулою (12.9).

Проведемо розрахунок коефіцієнту дисконтування:

Розмір кредиту дорівнює:

PV=3500 грн·37,115154=129903 грн.

Як бачимо, за розрахунками, після округлення, приведена вартість майже дорівнює сумі кредиту, але менша за суму кредиту на 97 грн. Таке зменшення може бути компенсовано при підписанні кредитного договору (контракту).

Відповідь: при ставці 36% за умови щомісячної сплати 3500 грн по кредиту в розмірі 130 тис. грн. строк сплати буде 10 років і 9 місяців с виплатою боржником кредиторові 97 грн в момент підписання кредитного договору (таку вимога з’явилася на підставі округлених розрахунків).

Читайте також:

1. Алгоритм розв’язання задачі
2. Алгоритм розв’язання розподільної задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз інформації та постановка задачі дослідження
11. Аналіз перед розв’язуванням задачі
12. Аналіз перед розв’язуванням задачі

Переглядів: 520