• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язування задачі

Розв’язування задачі ведемо у напрямку від першого вкладу (Р₁) до останнього вкладу (Р₄) в банк Б.

Розрахунок суми повернення по кредиту:

План погашення кредиту надано в табл. 13.11:

Таблиця 13.11

Результати розрахунку (план) погашення кредиту різними сумами (Р_k) за умов: формування фонду погашення кредиту через рік після одержання кредиту та в кінці строку дії фонду останній внесок (Р_k) здійснюється; тис. грн.

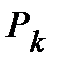
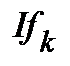
Рік (період - k)	Внески у фонд пога-шення кредиту,	Проценти, нараховані фондом погашення кредиту (f) у k–тому році (k-тому періоді),	Накопичення на кінець року (періоду k) у фонді погашення кредиту без внеску Р наростаючим підсумком,	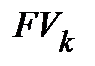Накопичення на кінець року (періоду k) у фонді погашення кредиту в сумі із внеском Р наростаючим підсумком, +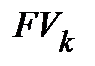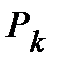
	100,000 200,000 300,000 275,212	15,000 47,250 99,338	115,000 362,250 761,588	100,000 315,000 652,250 1036,800
Всього	875,212	161,588	─	1036,8

Чисельні показники, які «наповнюють» табл. 13.11 та використовуються при побудові графіка повернення кредиту (рис. 13.8) «з’явилися» таким чином. Наданий далі механізм розрахунку має назву ─ табличний спосіб.

Спочатку обираємо будь-яку суму першого вкладу ─ показник Р₁. Обираємо суму Р₁ яка дорівнює 100 тис. грн (це сума вкладу в кінці першого року). Далі, нараховуємо на неї проценти в наступному році (за другий рік), процент дорівнює 15 тис. грн (100 тис. грн. 0,15), та в кінці другого року до Р₁ та нарахованих на Р₁ процентів ─ (Іf₂) приплюсовуємо вільно обрану суму наступного внеску ─ Р₂ =200 тис. грн. Отже, сума, що накопичилася на кінець другого року у фонді погашення кредиту наростаючим підсумком дорівнює 315 тис. грн (100 тис. грн + 15 тис. грн + 200 тис. грн). Впродовж третього року на суму 315 тис. грн нараховуються проценти, розмір яких дорівнює 47,25 тис. грн (315 тис. грн 0,15). В кінці третього року маємо суму, яка складається із суми на кінець попереднього, тобто другого року (315 тис. грн), процентів за третій рік (47,25 тис. грн), які разом ─ 362,25 тис. грн, та суми третього вкладу, який обрано в розмірі 300 тис. грн, тобто, маємо суму ─ 662,25 тис. грн (362,25 тис. грн + 300 тис. грн). Протягом останнього четвертого року на суму 662,25 тис. грн здійснюється нарахування процентів за ставкою 15 %. Розмір процентів за четвертий рік складає 99,338 тис. грн (662,25 тис. грн. 0,15 = 99,338 тис. грн). Загальна сума накопичень у фонді в кінці четвертого року дорівнює 761,588 тис. грн (662,25 тис. грн.+ 99,338 тис. грн). Сума грошей, якої не вистачає до загальної суми повернення по кредиту (FV = 1036,8 тис. грн), розраховується як різниця між сумою повернення по кредиту (FV) та накопиченою у фонді сумою (1036,8 тис. грн ─ 761,588 тис. грн) і в результаті є сумою 275,212 тис. грн. Ця сума і є останнім внеском (внеском Р₄) до фонду погашення кредиту.

Рисунок 13.8 - Графік повернення кредиту шляхом створення фонду погашення кредиту за умов: початок створення фонду ─ через рік після одержання кредиту; внески (Р_k) до фонду щорічні та різні; в кінці строку дії фонду останній внесок (Р_k) здійснюється; напрямок розв’язування ─ «від першого внеску…»; тис. грн. (Пояснення позначок на графіку дивись в табл. 13.11)

Табл. 13.11 та рис. 13.8 дають приклад розв’язування задачі 1 в межах першого напрямку, напрямку, коли обрання розміру вкладів починається з першого вкладу і йде за порядком до другого, третього і далі ─ до передостаннього, останній вклад не обирається, а розраховується за залишковим принципом.

Далі проведемо розв’язування тієї ж самої задачі 1 за другим напрямком ─ напрямком, коли обрання розміру вкладів в банк Б здійснюється за порядком від останнього вкладу (Р₄) до другого вкладу (Р₂), а перший вклад вільно не обирається, а розраховується як залишковий.

Початковим чисельним показником при розрахунку «від останнього вкладу…» виступає сума повернення по кредиту ─ FV. В задачі 1 це ─ сума FV = 1036,8 тис. грн. З іншого боку, застосовуючи умовні позначки, які використовуються в таблицях (напр. табл. 13.11) та в графіках (напр. рис. 13.8), сума повернення кредиту (FV) дорівнює сумі накопичень у фонді погашення кредиту на кінець четвертого року (FV₄), разом з останнім внеском (Р₄), тобто, FV = FV₄ + Р₄ =1036,8 тис. грн.

Хай обраний розмір останнього (4-го) внеску дорівнює Р₄=200,0 тис. грн. Тоді, розмір загального накопичення у фонді погашення кредиту на кінець 4-го року без врахування останнього внеску Р₄ дорівнює FV₄=836,8 тис. грн (1036,8 тис. грн ─ 200,0 тис. грн). Далі розрахунок має таку схему. Показник FV₄, який дорівнює 836,8 тис. грн, є сумою двох показників: ─ суми накопичень у фонді погашення кредиту на кінець третього року (FV₃), разом із внеском в кінці третього року (Р₃), тобто, FV₃+Р₃; ─ і процентів на цю суму накопичень, тобто, (FV₃ +Р₃) 0,15. Таким чином, маємо рівняння: (FV₃+Р₃)+(FV₃+Р₃) 0,15 = 836,8 тис. грн в якому показник в дужках ─ (FV₃+Р₃) є невідомою величиною. Розв’язання вказаного рівняння відносно невідомої дає результат: (FV₃+Р₃) = 727,652 тис. грн (836,8 тис. грн / (1+0,15) = 727,652 тис. грн). Тепер можемо розрахувати процент, який нарахований на суму (FV₃+Р₃) і який є процентом четвертого року ─ If₄. If₄ = =(FV₃+Р₃) 0,15=727,652 тис. грн 0,15=109,148 тис. грн.

Подальший розрахунок «вимагає» обрання розміру 3-го внеску. Обираємо Р₃=170 тис. грн та вводимо його в розрахунок. З попереднього абзацу розрахунків вже маємо: FV₃ + Р₃ = 727,652 тис. грн. Далі алгоритм розрахунку повторює попередній. Отже, розмір накопичення у фонді погашення кредиту на кінець 3-го року без врахування третього внеску Р₃ дорівнює FV₃ = 557,652 тис. грн (727,652 тис. грн ─ 170,0 тис. грн). Далі розрахунок повторює схему розрахунку попереднього абзацу. Показник FV₃, який дорівнює 557,652 тис. грн, є сумою двох показників: ─ суми накопичень у фонді погашення кредиту на кінець другого року (FV₂), разом із внеском в кінці другого року (Р₂), тобто, FV₂+Р₂; ─ і процентів на цю суму накопичень, тобто, (FV₂+Р₂) 0,15. Таким чином, маємо рівняння: (FV₂+Р₂)+(FV₂+Р₂) 0,15=557,652тис. грн в якому показник в дужках ─ (FV₂+Р₂) є невідомою величиною. Розв’язання вказаного рівняння відносно невідомої дає результат: (FV₂+Р₂) = 484,915 тис. грн (557,652 тис. грн / (1+0,15) = 484,915 тис. грн). Тепер можемо розрахувати процент, який нарахований на суму (FV₂+Р₂) і який є процентом третього року ─ If₃. If₃ = =(FV₂+Р₂) 0,15=484,915 тис. грн 0,15=72,737 тис. грн.

Обираємо розмір 2-го внеску ─ Р₂ =250,0 тис. грн. За розрахунком вже маємо: FV₂ + Р₂ = 484,915 тис. грн. Сума, яка накопичилася у фонді погашення кредиту на кінець 2-го року без врахування другого внеску Р₂ дорівнює FV₂ = 234,915 тис. грн (484,915 тис. грн ─ 250,0 тис. грн). Показник FV₂ є сумою двох показників: ─ суми накопичень у фонді погашення кредиту на кінець першого року (FV₁), разом із внеском в кінці першого року (Р₁), тобто, FV₁+Р₁; ─ і процентів на суму накопичень, тобто, (FV₁+Р₁) 0,15. Але, за умовами задачі, на кінець першого року накопичень не могло бути тому, що лише в кінці першого року було зроблено перший внесок (Р₁), отже, на кінець першого року FV₁ = 0. Таким чином, рівняння (FV₁+Р₁)+(FV₁+Р₁) 0,15 = 234,915 тис. грн перетворюється на рівняння Р₁+Р₁ 0,15 = 234,915 тис. грн, в якому показник Р₁ є невідомою величиною. Розв’язання вказаного рівняння дає показник Р₁, тобто, це розмір першого внеску, який дорівнює Р₁=204,274 тис. грн (234,915 тис. грн / (1+0,15)= = 204,274 тис. грн). Тепер можемо розрахувати процент, який нараховується на внесок Р₁ і який є процентом другого року ─ If₂. If₂ = Р₁ 0,15 = 204,274 тис. грн 0,15=30,641 тис. грн.

Наведений вище алгоритм формування фонду погашення кредиту нерівними вільно обраними внесками зі застосуванням напрямку «від останнього вкладу…» використовується як розрахунковий механізм заповнення таблиці, яка є одночасно і розрахунком і планом погашення кредиту. Табличний спосіб розрахунку передбачає використання саме такого алгоритму розрахунку. Всі данні занесені в табл. 13.12 та за розрахованими показниками побудовано графік ─ рис. 13.9.

Таблиця 13.12

Результати розрахунку (план) погашення кредиту різними сумами (Р_k) за умов: формування фонду погашення кредиту через рік після одержання кредиту; в кінці строку дії фонду останній внесок (Р_k) здійснюється; напрямок розв’язування ─ «від останнього внеску…»; данні в таблиці ─ тис. грн.

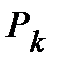
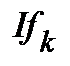
Рік (період - k)	Внески у фонд пога-шення кредиту,	Проценти, нараховані фондом погашення кредиту (f) у k–тому році (k-тому періоді),	Накопичення на кінець року (періоду k) у фонді погашення кредиту без внеску Р наростаючим підсумком,	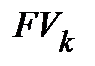Накопичення на кінець року (періоду k) у фонді погашення кредиту в сумі із внеском Р наростаючим підсумком, +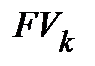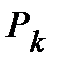
	204,274 250,000 170,000 200,000	30,641 72,737 109,148	234,915 557,652 836,800	204,274 484,915 727,652 1036,800
Всього	824,274	212,526	─	1036,8

Рисунок 13.9 - Графік повернення кредиту шляхом створення фонду погашення кредиту за умов: початок створення фонду ─ через рік після одержання кредиту; внески (Р_k) до фонду щорічні та різні; в кінці строку дії фонду останній внесок (Р_k) здійснюється; напрямок розв’язування ─ «від останнього внеску…»; тис. грн. (Пояснення позначок на графіку дивись в табл. 13.12)

Читайте також:

1. Алгоритм розв’язання задачі
2. Алгоритм розв’язання розподільної задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз інформації та постановка задачі дослідження
11. Аналіз перед розв’язуванням задачі
12. Аналіз перед розв’язуванням задачі

Переглядів: 564