Алгоритм СМ у формі тотожних перетворень

Реалізацію алгоритму СМ у формі тотожних перетворень проілюструємо на прикладі 1.1. в якому потрібно знайти найбільше значення функції 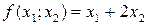при обмеженнях

, (1.10)

де х₁– кількість прикрас виду А₁, х₂ – кількість прикрас виду А₂, які виготовить майстерня. Ввівши допоміжні змінні 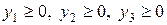(їх кількість дорівнює кількості обмежень в задачі), запишемо дану задачу в канонічному вигляді: знайти найбільше значення функції

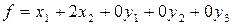(1.11)

при обмеженнях

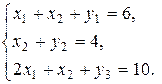(1.12)

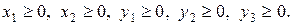(1.13)

Виразимо з (1.12) базисні змінні і перепишемо задачу (1.11) – (1.12) у вигляді 0-рівнянь.

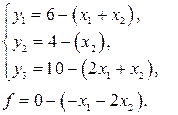(1.14)

На початку виробничої діяльності продукція не виготовляється, тому х₁= 0, х₂= 0 і f = 0. Даний розв’язок є опорним. Як видно із (1.11), спочатку потрібно здійснювати випуск продукції х₂ (вартість виробу А₂ більша за вартість виробу А₁), тобто збільшувати х₂.

Стовпчик коефіцієнтів при х₂ в системі обмежень (1.14) будемо називати розв’язуючим, змінні у₁, у₂, у₃ – базисними змінними, а х₁ і х₂ – небазисними.

Оскільки ми збільшуємо х₂, то х₁=0 із (1.14), матимемо

Так як змінні , то

(1.15)

Максимальне збільшення х₂ можливе до 4. Дійсно, 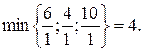Цей рядок із (1.14), для якого досягається найменше відношення вільних членів до додатних коефіцієнтів розв’язуючого стовпчика, назвемо розв’язуючим. З нього одержуємо (змінна стає базисною, а на її місце переходить змінна ). Підставляючи в (1.14), одержимо

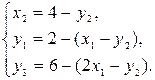(1.16)

(1.17)

Покладаючи небазисні змінні , одержимо наступний опорний розв’язок: і .

Як видно з (1.17), наступне збільшення значення f можливе за рахунок збільшення змінної . Маємо Друге рівняння із (1.16) є розв’язуючим. З нього . Підставивши в (1.16) і (1.17), одержимо

(1.18)

(1.19)

Нехай y₁=0, y₂=0. Тоді 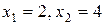і .

Як видно з (1.19), наступне збільшення f неможливе. Тому можна зробити наступний висновок: опорний розв’язок буде оптимальним, якщо у виразі в дужках для цільової функції (1.19) відсутні від’ємні коефіцієнти при небазисних змінних у₁ і у₂. Даний висновок за умови узагальнення може бути прийнятий за критерій оптимальності опорного розв’язку.

Запропонований підхід до розв’язування ЗЛП використовується рідко (в основному для ЗЛП з двома, трьома змінними), оскільки вимагає виконання великої кількості алгебраїчних перетворень цільової функції і системи обмежень.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Симплексний метод розв’язування ЗЛП (СМ)	\|	Табличний запис ЗЛП. Алгоритм СМ для ЗЛП, представлених в симетричній формі.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.02 сек.