
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Алгоритм Гоморі
Р. Гоморі для отримання цілочислових розв’язків розробив алгоритм, який використовує відому симплексну процедуру. Як і в методі відтинаючих площин, спочатку ЗЦЛП розв’язується без умови цілочисельності. Якщо отриманий розв’язок є цілим, то задача розв’язана. В протилежному випадку до обмежень задачі додається ще одне, яке ми назвали правильним відтинанням.
Після цього отримана ЗЛП розв’язується з врахуванням нового обмеження. Потім, якщо потрібно, додається ще одне відтинаюче обмеження і т.д. до отримання повністю цілочислового розв’язку задачі.
Припустимо, що в результаті розв’язування СМ канонічної ЗЛП (1.41)–(1.43) одержали оптимальний план  , в якому, наприклад,
, в якому, наприклад,  – неціла компонента. Нерівність
– неціла компонента. Нерівність
 , (1.45)
, (1.45)
сформована за k-им рядком, володіє всіма властивостями правильного відтинання.
В (1.45) символ  означає дробову частину числа.
означає дробову частину числа.
Визначення.1.21. Дробовою частиною  числа а називають різницю між цим числом і його цілою частиною
числа а називають різницю між цим числом і його цілою частиною 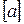 , тобто найменшим цілим, яке не перевищує а.
, тобто найменшим цілим, яке не перевищує а.
Наприклад, якщо  , то
, то 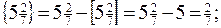 якщо
якщо  , то
, то 
Для розв’язування ЗЦЛП (1.41)–(1.44) використовують наступний алгоритм.
1. СМ розв’язуємо ЗЛП (1.41)–(1.43). Якщо всі компоненти оптимального плану цілі, то він є оптимальним і для ЗЦЛП (1.41)–(1.44). Якщо ЗЛП (1.41)–(1.43) не має розв’язку, то і ЗЦЛП (1.41)–(1.44) також не має розв’язку. Якщо ж серед компонент оптимального плану є нецілі, то переходимо до п.2.
2. Серед нецілих компонент вибираємо компоненту з найбільшою дробовою частиною і за відповідним рядком симплексної таблиці, яка містить нецілочисловий оптимальний план, будуємо правильне відтинання (1.45).
3. Нерівність (1.45), введенням додаткової невід’ємної цілочислової змінної, перетворюємо в еквівалентне рівняння і включаємо його в симплексну таблицю з нецілочисловим оптимальним планом.
4. Одержану розширену ЗЛП розв’язуємо СМ. Якщо одержаний оптимальний план буде цілочисловим, то ЗЦЛП (1.41)–(1.44) розв’язана. В іншому разі повертаємося до п.2.
Якщо задача має розв’язок в цілих числах, то після скінченного числа ітерацій оптимальний цілочисловий план буде знайдений. Якщо ж в процесі розв’язування з’явиться рядок з нецілим вільним членом і рештою цілих коефіцієнтів, то відповідне рівняння не має розв’язку в цілих числах. В цьому випадку і дана задача не має цілочислового оптимального плану.
Приклад 1.13.Знайти найбільше значення функції 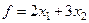 при обмеженнях
при обмеженнях
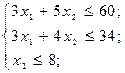
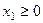 ;
; 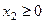 ,
,  ,
, 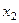 – цілі числа.
– цілі числа.
Розв’язок. Розв’язуючи задачу без обмеження цілісності змінних СМ, одержали оптимальний план.
 За рядком змінної х1, яка набула нецілочислового значення в оптимальному плані, будуємо обмеження (1.45)
За рядком змінної х1, яка набула нецілочислового значення в оптимальному плані, будуємо обмеження (1.45)
 ,
, 
Ввівши додаткову цілочислову змінну  , одержимо
, одержимо 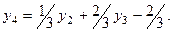 Доповнимо попередню таблицю ще одним рядком і провівши один крок перетворень Жордана-Гаусса, матимемо:
Доповнимо попередню таблицю ще одним рядком і провівши один крок перетворень Жордана-Гаусса, матимемо:
– 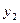
| – 
| 
| 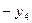
| 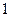
| |||||

| –1 | –1 | 
| – 
| – 
| ||||
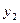
| 
| 
| 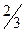
| 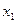
| –2 | ||||

| 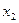
| – 
| 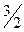
| ||||||
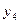
| – 
| – 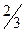
| – 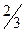
| 
| 
| – 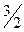
| |||
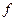
| 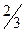
| 
| 25 
| 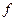
| 
| 
|
З останньої таблиці отримуємо оптимальний цілочисловий план 
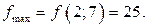
Контрольні запитання та задачі
1. Які задачі відносять до ЗЦЛП?
2. На які види поділяються ЗЦЛП?
3. Як формулюється ЗЦЛП?
4. В чому різниця між математичними моделями ЗЛП і ЗЦЛП?
5. Чому методи розв’язування ЗЛП не придатні для розв’язування ЗЦЛП?
6. Які ви знаєте методи розв’язування ЗЦЛП?
7. Яке обмеження називається правильним відтинанням?
8. В чому суть методу гілок і границь?
9. Що називається дробовою частиною числа а?
10. Як будується правильне відтинання в алгоритмі Гоморі?
11. Вкажіть основні пункти алгоритму Гоморі.
12. Методом відтинаючих площин знайти цілі розв’яки ЗЛП, при яких функція 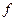 досягає найбільшого значення
досягає найбільшого значення
а)

| б)
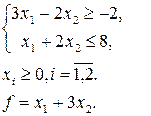
| в)

|
13. Методом гілок і границь знайти цілі розв’язки ЗЛП, при яких функція 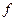 досягає найбільшого значення
досягає найбільшого значення
а)
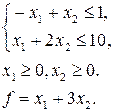
| б)

| с)
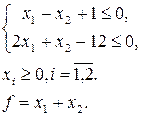
|
14. Використовуючи алгоритм Гоморі, знайти цілі розв’язки ЗЛП, при яких функція 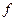 досягає найбільшого значення
досягає найбільшого значення
а)

| б)
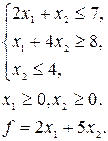
| в)

| |
г)
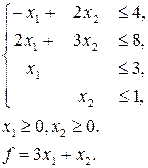
| д)
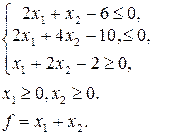
|
Читайте також:
- Rete-алгоритм
- Алгоритм
- Алгоритм
- Алгоритм 1.
- Алгоритм 2
- Алгоритм RLE
- Алгоритм безпосередньої заміни
- Алгоритм Берлекемпа-Мессі
- Алгоритм відшукання оптимального плану.
- Алгоритм Дейкстри.
- Алгоритм Деккера.
| <== попередня сторінка | | | наступна сторінка ==> |
| Метод гілок і границь | | | РОЗДІЛ 2. ГРАФИ І МЕРЕЖІ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |