• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Метод гілок і границь

Нехай потрібно максимізувати функцію 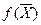за умови, що 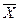належить деякій скінченній множині G. Перш за все шукаємо верхню границю 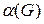функції 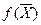на множині всіх планів G. Далі множину G певним чином розбиваємо на декілька неперетинаючих підмножин . Потім на одержаних підмножинах шукаємо верхні границі функції 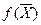. Нехай 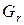– підмножина, для якої , де Якщо тепер на цій підмножині знайдеться таке , що , то задача розв’язана: план є оптимальним. Якщо такий план не знайдено, то процес розбиття продовжуємо, починаючи з множини 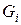, для якої – найбільше. Оскільки множина всіх планів скінченна, то оптимальний план після скінченного числа розбиттів буде знайдений.

Приклад 1.12. Методом гілок і границь знайти найбільше значення функції 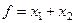при обмеженнях:

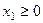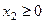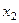; ; , – цілі числа.

Розв’язок. Будуємо область допустимих планів.

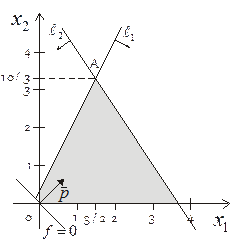
Рис. 1.12

Якщо розглядати дану задачу без умови цілочисельності, то найбільше значення досягається в точці і дорівнює 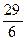. . 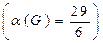Оскільки, , то розіб’ємо G на дві частини: одна з них містить ті допустимі плани, в яких , а в другу увійдуть допустимі плани з 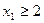. При цьому не буде втрачено жодного допустимого цілочислового розв’язку.

Знайдемо для функції 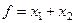верхні межі в областях і : і . Для цього розв’яжемо дві ЗЛП: знайти найбільше значення функції при обмеженнях

а) б)

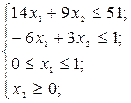
де , 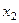– цілі числа. де , 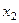– цілі числа.

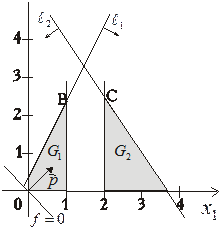
Рис.1.13

Розв’язуючи дані задачі без умови цілочисельності, встановлюємо, що найбільше значення функції f задачі а) досягається в точці і дорівнює 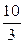, в задачі б) – в точці і дорівнює 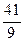. Оскільки > 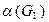, то розбиваємо на дві неперетинаючі підмножини і , а за додаткові обмеження візьмемо спочатку 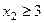, а потім . Таким чином, приходимо до задачі: знайти найбільше значення функції при обмеженнях

в) г)

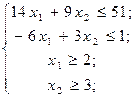
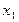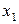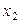, – цілі числа. , – цілі числа.

Рис.1.14

З рисунка видно, що задачу в) можна не розглядати, оскільки вона не має жодного допустимого плану; що стосується задачі г) то в області точка 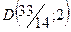задає її нецілочисловий оптимальний план з = = > .

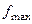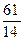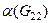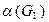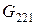Розбивши на дві неперетинаючі підмножини і , і взявши за додаткові обмеження спочатку , а потім , прийдемо до наступної пари ЗЛП: знайти найбільше значення функції при обмеженнях

д) е)

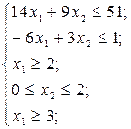
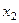, – цілі числа. , 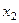– цілі числа.

Оптимальні плани задач д) і е) без умови цілочисельності визначаються точками і і = = 4. Оскільки , то ми можемо стверджувати, що в точках E і F функція дійсно досягає найбільшого значення..

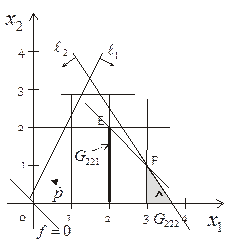
Рис.1.15

Зауваження 1.10. При розв’язуванні конкретних задач методом гілок і границь оптимум нерідко вдається відшукати доволі швидко. Проте цю процедуру часто доводиться виконувати багато разів, оскільки в ході обчислень виникає необхідність в неодноразовому поверненні назад в пошуках нових гілок “дерева” можливих варіантів. У прикладі, який ми розглядали, нам не доводилось цього робити тільки тому, що > , а потім = > .

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
5. I. Метод рiвних вiдрiзкiв.
6. VII. Нахождение общего решения методом характеристик
7. А. науковий факт, b. гіпотеза, с. метод
8. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
9. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
10. Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
11. АгротехнІЧНИЙ метод
12. Адаптовані й специфічні методи дослідження у журналістикознавстві

Переглядів: 1042