
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Алгоритм СМ для ЗЛП, представлених в загальному виді
Характерним для задач, представлених в загальному виді, є те, що серед обмежень на змінні є обмеження  і
і  , а також можуть бути вільні змінні. Для цих задач розв’язування починається з пошуку опорного розв’язку. Тому, якщо знайдений будь-який опорний розв’язок, то його оптимізація зводиться до методу, що описаний в попередньому пункті.
, а також можуть бути вільні змінні. Для цих задач розв’язування починається з пошуку опорного розв’язку. Тому, якщо знайдений будь-який опорний розв’язок, то його оптимізація зводиться до методу, що описаний в попередньому пункті.
Отримання опорного розв’язку для задач з обмеженням типу  і
і 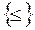 .
.
При записі даних задачі в симплексну таблицю серед вільних членів задачі будуть і від’ємні. Щоб отримати опорний розв’язок, їх потрібно зробити невід’ємними. Для цього серед них вибираємо найбільший за модулем від’ємний. Потім в даному рядку вибираємо будь-який від’ємний коефіцієнт (якщо такі відсутні, то система обмежень є суперечливою), який визначить розв’язуючий стовпчик. Далі складаємо відношення вільних членів bi до однойменних за знакомкоефіцієнтів розв’язуючого стовпчика. Найменше відношення визначить розв’язуючий рядок. На перетині розв’язуючого рядка і стовпчика буде знаходитись розв’язуючий елемент. Тут можливі два випадки:
– розв’язуючий елемент належить розглядуваному рядку;
– розв’язуючий елемент не належить розглядуваному рядку.
В першому випадку після здійснення одного кроку перетворень Жордана-Гаусса відповідний вільний член стане додатним. Аналогічно здійснюємо перетворення з від’ємними вільними членами, що залишились. Коли всі вільні члени стануть невід’ємні, то розв’язок, який представляється даною симплекс-таблицею, буде опорним. Для отримання оптимального розв’язку поступаємо як в пункті 1.4.3 даного параграфу.
В другому випадку після виконання одного кроку перетворень Жордана-Гаусса розглядуваний вільний член може і далі залишатися від’ємним. Тоді реалізацію вибору розв’язуючого елемента при від’ємних вільних членах виконуємо знову. За скінченного числа кроків модифікованих виключень одержимо опорний розв’язок, або покажемо, що ЗЛП його не має.
Зауваження 1.7. При виконанні перетворень Жордана-Гаусса кількість від’ємних вільних членів не збільшиться.
Отримання опорного розв’язку для задач з обмеженням типу 
Для таких задач базисні змінні рівні нулю. Для їх виключення ці змінні потрібно перевести наверх таблиці (тобто вивести з базису). Цей процес називають виключенням 0-рядка.
Для виключення 0-рядків розв’язуючий елемент вибирають наступним чином. У відповідних 0-рядках симплексної таблиці вільні члени роблять невід’ємними. Якщо серед вільних членів є від’ємні, то елементи відповідного рядка домножують на (–1). В симплексній таблиці вибираємо будь-який 0-рядок і в ньому додатний елемент, який визначить розв’язуючий стовпчик. Далі складаємо відношення вільних членів до однойменних за знаком коефіцієнтів розв’язуючого стовпчика, найменше з яких визначить розв’язуючий рядок. На перетині розв’язуючого стовпчика і рядка знаходиться розв’язуючий елемент. Тут можливі два випадки:
– розв’язуючий елемент належить розглядуваному 0-рядку;
– розв’язуючий елемент не належить розглядуваному 0-рядку.
В першому випадку після здійснення одного кроку перетворень Жордана-Гаусса “0” переходить наверх симплексної таблиці, і стовпчик, який йому відповідає, виключаємо з розгляду (викреслюємо). Далі виключаємо наступний 0-рядок. За скінченне число кроків ми повністю виключимо всі 0-рядки або покажемо, що ЗЛП розв’язку не має. Після виключення всіх 0-рядків ми можемо отримати опорний розв’язок (всі вільні члени невід’ємні), або знаходитися на етапі пошуку опорного розв’язку (серед вільних членів є від’ємні). В такому випадку ми повинні реалізувати алгоритм отримання опорного розв’язку ЗЛП, наведений вище.
У випадку, коли розв’язуючий елемент не належить розглядуваному 0-рядку, ми повинні з ним виконати один крок перетворень Жордана-Гаусса і реалізацію алгоритму виключення 0-рядка почати спочатку.
Зауваження 1.8. Ми розглядали ЗЛП, в яких потрібно знайти найбільше значення цільової функції. Якщо ж потрібно знайти найменше значення, то достатньо замінити  на –
на –  , оскільки
, оскільки  , і повторити вищенаведені міркування.
, і повторити вищенаведені міркування.
Приклад 1.3. Знайти найменше значення функції 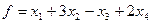 при обмеженнях
при обмеженнях


Розв’язок.Помноживши друге обмеження системи на (–1) і врахувавши, що 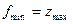 , де
, де  , умову задачі перепишемо так: знайти найбільше значення функції
, умову задачі перепишемо так: знайти найбільше значення функції 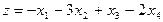 при обмеженнях
при обмеженнях


Ввівши базисні змінні у1, у2, у3 так, щоб

перейдемо до симплексної таблиці:
| –x1 | –x2 | –x3 | –x4 | ||
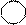 2 2
| –2 | ||||
| y2 | –3 | –1 | –3 | ||
| y3 | –1 | ||||
| z | –1 | ||||
| |
Оскільки в симплексній таблиці є 0-рядок, то розв’язок починаємо з його виключення. Вибираємо в ньому будь-який додатній елемент, наприклад 2, який буде розв’язуючим, оскільки є тільки одне відношення однойменних за знаком вільних членів до елементів розв’язуючого стовпчика 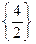 . Виконавши один крок перетворень Жордана-Гаусса, отримаємо:
. Виконавши один крок перетворень Жордана-Гаусса, отримаємо:
| -x1 | –x3 | –x4 | |||
| х2 | 1/2 | 1/2 | –1 | 1/2 | |
| y2 | –7/2 | –1/2 | 1/2 | –5 | |
| y3 | –1 | ||||
| z | –1/2 | –3/2 | 1/2 | –6 |
Викресливши в даній таблиці відповідний 0-стовпчик, дістанемо
| –x1 | –x3 | –x4 | ||
| х2 |  1/2 1/2
| –1 | 1/2 | |
| y2 | –7/2 | 1/2 | –5 | |
| y3 | –1 | |||
| z | –1/2 | 1/2 | –6 | |
| |
В цій таблиці серед вільних членів є від’ємний (–5) і виписати опорний розв’язок неможливо. Тому в рядку, що містить від’ємний вільний член, вибираємо будь–який від’ємний коефіцієнт, наприклад (–7/2). Він визначить розв’язуючий стовпчик. Складаємо відношення вільних членів до однойменних за знаком коефіцієнтів розв’язуючого стовпчика і знаходимо 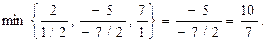 Другий рядок розв’язуючий, а елемент (–7/2) – розв’язуючий. Виконавши один крок перетворень Жордана-Гаусса, матимемо
Другий рядок розв’язуючий, а елемент (–7/2) – розв’язуючий. Виконавши один крок перетворень Жордана-Гаусса, матимемо
 –у2 –у2
| –x3 | –x4 | ||
| х2 | 1/7 | –1 | 4/7 | 9/7 |
| x1 | –2/7 | –1/7 | 10/7 | |
| y3 | 2/7 | –1 | 15/7 | 39/7 |
| z | –1/7 | 3/7 | –37/7 | |
| |
Оскільки серед вільних членів відсутні від’ємні коефіцієнти, то отримаємо опорний план: 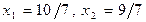 ,
, 
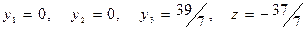 , який не є оптимальним, оскільки в z-рядку є від’ємні елементи.
, який не є оптимальним, оскільки в z-рядку є від’ємні елементи.
Коефіцієнт (–1/7) z-рядка визначає розв’язуючий стовпчик. Для знаходження розв’язуючого рядка шукаємо  Отже, перший рядок буде розв’язуючим, а (1/7) – розв’язуючим елементом. Після проведення одного кроку перетворень Жордана-Гаусса приходимо до таблиці
Отже, перший рядок буде розв’язуючим, а (1/7) – розв’язуючим елементом. Після проведення одного кроку перетворень Жордана-Гаусса приходимо до таблиці

| 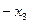
| 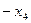
| ||
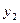
| ||||
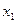
| ||||

| ||||

| –4 |
Розв’язок  буде оптимальним. Враховуючи те, що
буде оптимальним. Враховуючи те, що  , отримаємо
, отримаємо 
Читайте також:
- Rete-алгоритм
- Алгоритм
- Алгоритм
- Алгоритм 1.
- Алгоритм 2
- Алгоритм RLE
- Алгоритм безпосередньої заміни
- Алгоритм Берлекемпа-Мессі
- Алгоритм відшукання оптимального плану.
- Алгоритм Гоморі
- Алгоритм Дейкстри.
- Алгоритм Деккера.
| <== попередня сторінка | | | наступна сторінка ==> |
| Табличний запис ЗЛП. Алгоритм СМ для ЗЛП, представлених в симетричній формі. | | | Реалізація алгоритму СМ для ЗЛП з вільними змінними |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |