
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Послідовність виконання роботи
Зверніть увагу на систему частинок, що рухаються в замкнутому об’ємі ліворуч на екрані (на рисунку 20.4 наведено інтерфейс програми). Вони абсолютно пружно зіштовхуються одна з одною і зі стінками посудини. Дана система є гарною "механічною" моделлю ідеального газу. У процесі досліджень можна зупиняти рух усіх молекул (при натисканні кнопки "Стоп" мишкою) і отримати як би "миттєві фотографії", на яких виділяються зеленим кольором молекули (точки), швидкості яких лежать у заданому діапазоні ∆v поблизу заданої швидкості v (тобто, що мають швидкості від v до v+∆v).
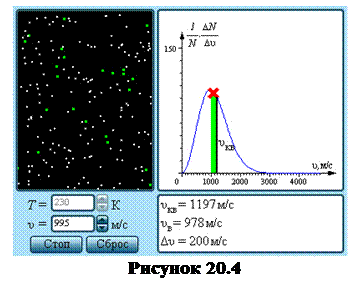 1. Натисніть кнопку «Стоп» і порахуйте загальну кількість молекул у системі, які мають швидкість в інтервалі ∆v. Натисніть «Старт», через деякий час знову зробить «миттєву фотографію» і знову підрахуйте відповідну кількість молекул. Тричі порахуйте розмір системи і знайдіть середнє значення N.
1. Натисніть кнопку «Стоп» і порахуйте загальну кількість молекул у системі, які мають швидкість в інтервалі ∆v. Натисніть «Старт», через деякий час знову зробить «миттєву фотографію» і знову підрахуйте відповідну кількість молекул. Тричі порахуйте розмір системи і знайдіть середнє значення N.
2. Задайте температуру Т1, зазначену в таблиці 1 для вашого варіанту. Після встановлення температури встановіть значення швидкості з таблиці 2. Будемо рахувати кількість молекул, швидкості яких знаходяться у заданому діапазоні (∆v = 200м/с) поблизу заданої швидкості. Для цього натисніть кнопку «Стоп» і підрахуйте кількість виділених частинок. Результат запишить в таблицю 2. Натисніть кнопку «Старт» і через декілька секунд отримайте ще одну фотографію (натиснувши кнопку «Стоп») і порахуйте кількість частинок із заданою швидкістю. Результати 5-ти вимірювань для кожної швидкості запишіть у таблицю 20.2.
3. Потім встановіть інше значення температури Т2 з таблиці 1 і повторіть вимірювання, записуючи результати у таблицю 20.3, аналогічну таблиці 20.2.
4. Міняючи значення температури Т від 150К до 800К із кроком в 50К. Отримані в програмі значення середньої квадратичної та найбільш імовірної швидкості занесіть в таблицю 4. В 4-й рядок таблиці занесіть квадрат найбільш імовірної швидкості.
Таблиця 20.3– Результати вимірів для T = __ K
| v[км/с]= | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 |
| DN1 | ||||||||||||
| DN2 | ||||||||||||
| DN3 | ||||||||||||
| DN4 | ||||||||||||
| DN5 | ||||||||||||
| DNСЕР |
Таблиця 20.4 – Залежність найбільш імовірної та середньої квадратичної швидкості від температури
| Т, К | … | … | |||
| vсер. кв, м/с | |||||
| vім, м/с | |||||
| v2ім, м2/с2 |
Читайте також:
- II. Вимоги безпеки перед початком роботи
- II. Вимоги безпеки праці перед початком роботи
- III. Виконання бюджету
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
- IV. Вимоги безпеки під час роботи на навчально-дослідній ділянці
- IV. Вимоги безпеки після закінчення роботи
- IV. Вимоги безпеки після закінчення роботи
- IІІ. Послідовність виконання курсової роботи
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розподіл Максвелла. | | | Обробка результатів |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |