РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема(друга важлива границя)
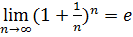– це деяке число, яке наближено дорівнює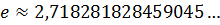 
Приклад 5 . Обчислити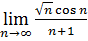 
.
Послідовність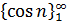 
обмежена, а оскільки 
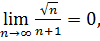тому 
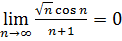
Приклад 6. Обчислити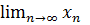 
, де 
Запишемо оцінку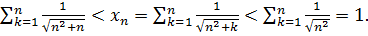 
Оскільки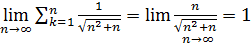 
, то згідно з теоремою про проміжну послідовність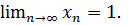 
Приклад 7. Обчислити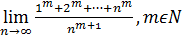 
Застосуємо теорему Штольца, зауваживши, що 
монотонно зростає для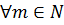 
і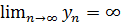 
. При цьому
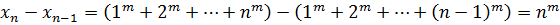і
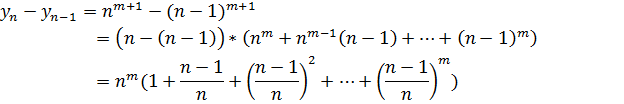
За теоремою Штольца
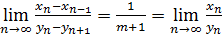, отже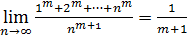 
Приклад 8. Обчислити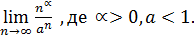 
Оскільки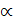 
-фіксоване, то 
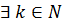таке, що 
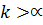. Розглянемо послідовність 
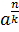і застосуємо для неї нерівність Бернуллі.
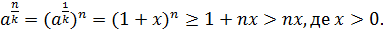Звідси 
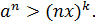Тоді
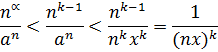
Розглянемо довільне 
. Розв’яжемо нерівність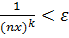 
відносно 
. Одержимо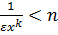 
. Таким чином, для довільного 
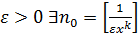таке, що для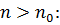 
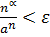. За означенням границі послідовності це означає, що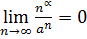 
Приклад 9. Обчислити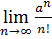 
Для фіксованого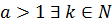 
таке, що 
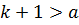. Тоді
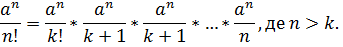
Звідси одержуємо, що
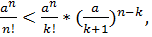де 
і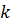 
– фіксовані числа. Як показано в прикладі 7,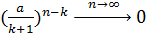 
Відповідь: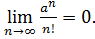 
Приклад 10. Обчислити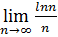 
Розглянемо довільне
Нерівність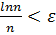 
еквівалетна нерівності 
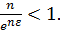Позначимо 
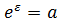. Як показано в прикладі 8, 
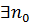таке, що для 
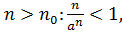отже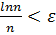
Відповідь: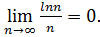 
Приклад 11. Обчислити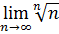 
Розглянемо n чисел: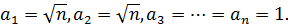 
Запишемо для них нерівність Коші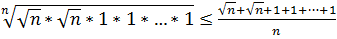 
Звідси одержимо, що
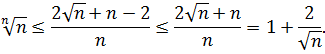
Оскільки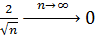 
, то, використавши теорему про проміжну послідовність, з нерівності 
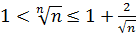одержимо, що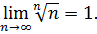 
Завдання 1
Користуючись означенням границы послідовності за Коші довести, що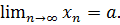 
1. 
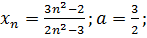
2. 
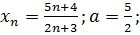
3. 
4. 
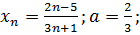
5. 
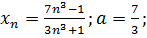
6. 
7. 
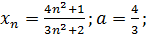
8. 
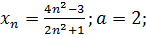
9. 
10. 
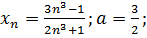
11. 
12. 
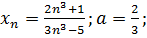
13. 
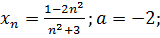
14. 
15. 
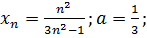
16. 
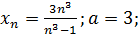
17. 
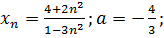
18. 
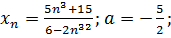
19. 
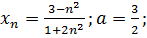
20. 
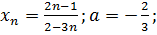
21. 
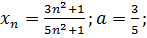
22. 
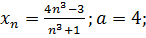
23. 
24. 
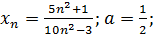
25. 
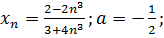
26. 
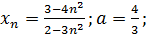
27. 
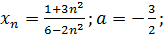
28. 
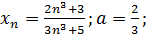
29. 
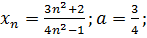
30. 
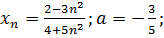
Завдання 2
Користуючись критерієм Коші збіжності послідовності, довести збіжність наступних послідовностей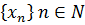 
, або користуючись запереченням критерію Коші збіжності послідовності, довести розбіжність послідовності 
.
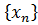1. 
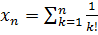
2. 
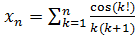
3. 
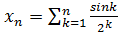
4. 
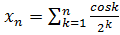
5. 
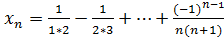
6. 
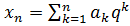, де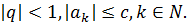 
7. 
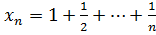
8. 
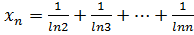
9. 
10. 
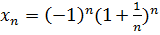
11. 
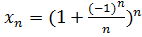
12. 
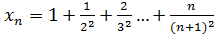
13. 
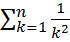
14. 
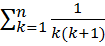
15. 
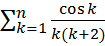
16. 
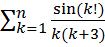
17. 
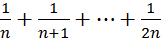
18. 
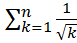
19. 
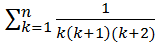
20. 
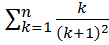
21. 
22. exp((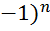 
n)
23. 
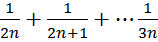
24. 
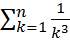
25. 
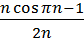
26. 
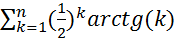
27. 
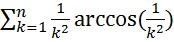
28. sin(n)
29. cos(n)
30. tg(n)
Завдання 3
Знайти границю:
1. 
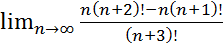
2. 
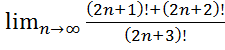
3. 
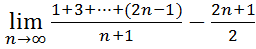
4. 
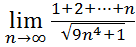
5. 
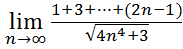
6. 
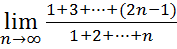
7. 
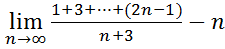
8. 
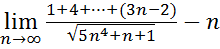
9. 
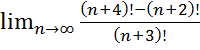
10. 
11. 
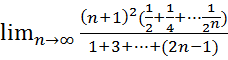
12. 
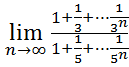
13. 
14. 
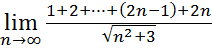
15. 
16. 
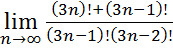
17. 
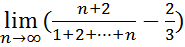
18. 
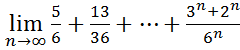
19. 
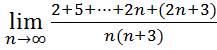
20. 
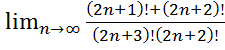
21. 
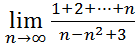
22. 
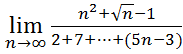
23. 
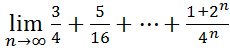
24. 
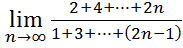
25. 
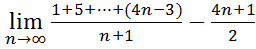
26. 
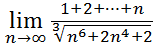
27. 
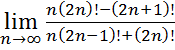
28. 
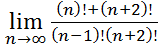
29. 
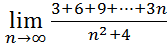
30. 
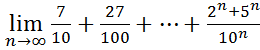
Завдання 4
Знайти границі:
1. 
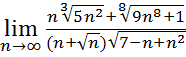
2. 
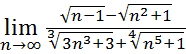
3. 
4. 
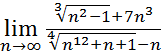
5. 
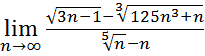
6. 
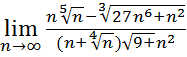
7. 
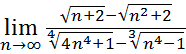
8. 
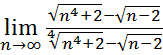
9. 
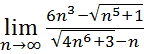
10. 
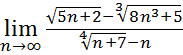
11. 
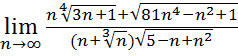
12. 
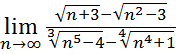
13. 
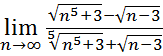
14. 
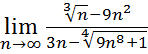
15. 
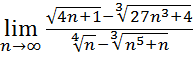
16. 
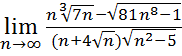
17. 
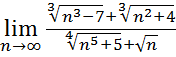
18. 
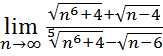
19. 
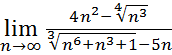
20. 
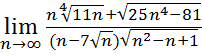
21. 
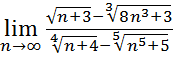
22. 
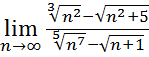
23. 
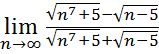
24. 
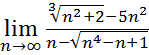
25. 
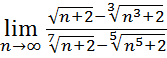
26. 
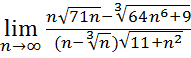
27. 
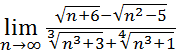
28. 
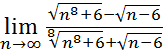
29. 
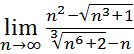
30. 
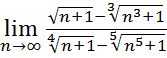
Завдання 5
Знайти границі:
1. 
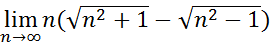
2. 
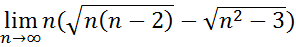
3. 
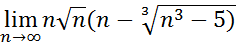
4. 
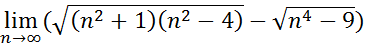
5. 
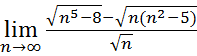
6. 
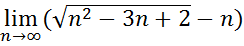
7. 
8. 
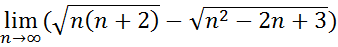
9. 
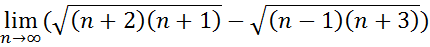
10. 
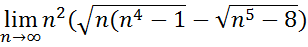
11. 
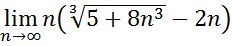
12. 
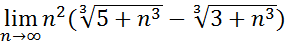
13. 
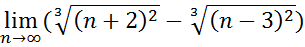
14. 
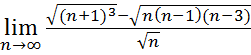
15. 
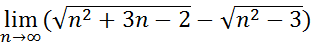
16. 
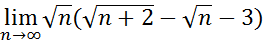
17. 
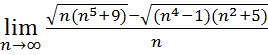
18. 
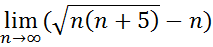
19. 
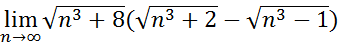
20. 
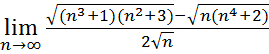
21. 
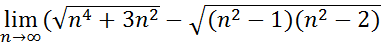
22. 
23. 
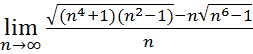
24. 
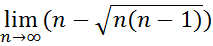
25. 
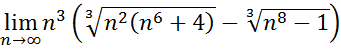
26. 
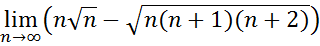
27. 
28. 
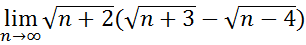
29. 
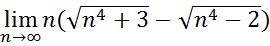
30. 
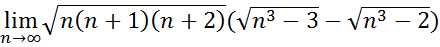
Завдання 6
Знайти границю:
1. 
.
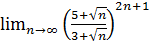2. 
.
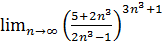3. 
.
4. 
.
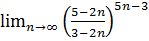5. 
.
6. 
.
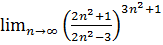7. 
.
8. 
.
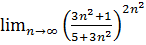9. 
.
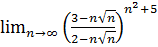10. 
.
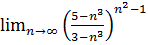11. З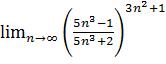 
.
12. 
.
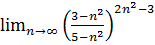13. 
.
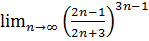14. 
.
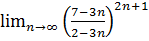15. 
.
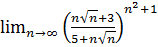16. 
.
17. 
.
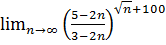18. 
.
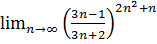19. 
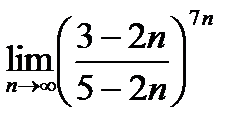
20. 
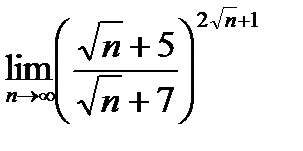
21. 
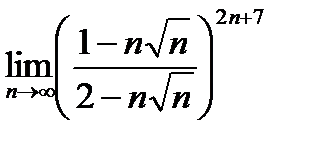
22. 
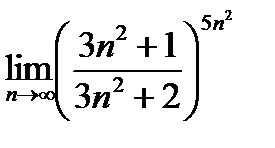
23. 
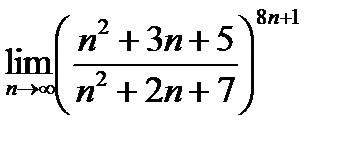
24. 
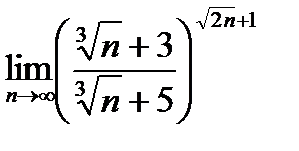
25. 
26. 
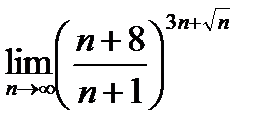
27. 
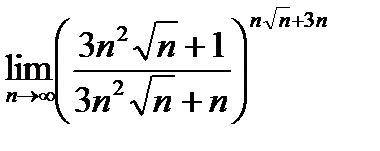
28. 
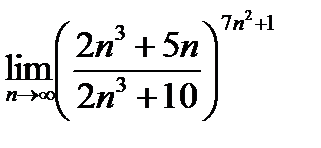
29. 
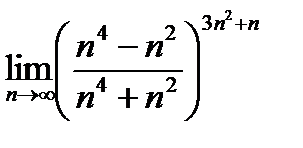
30. 
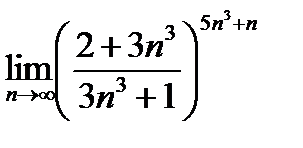
Завдання 7
Знайти границі:
1. 
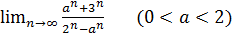
2. 
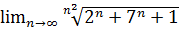
3. 
4. 
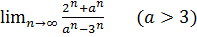
5. 
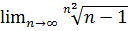
6. 
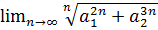
7. 
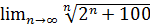
8. 
9. 
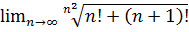
10. 
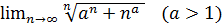
11. 
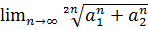
12. 
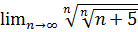
13. 
14. 
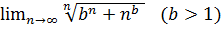
15. 
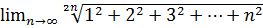
16. 
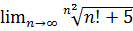
17. 
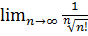
18. 
.
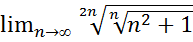19. 
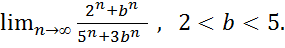
20. 
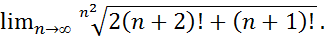
21. 
.
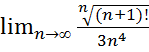22. 
.
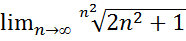23. 
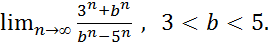
24. 
.
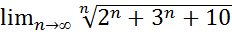25. 
.
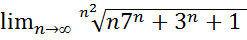26. 
.
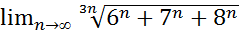27. 
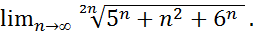
28. 
.
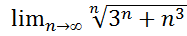29. 
.
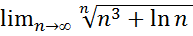30. 
.
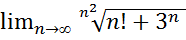Завдання 8
Знайти границю:
1. 
.
2. 
.
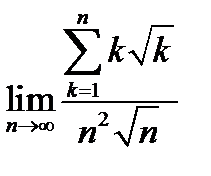3. 
.
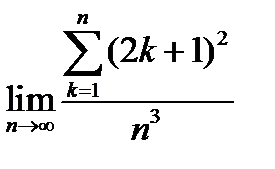4. 
.
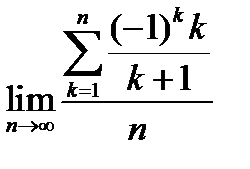5. 
.
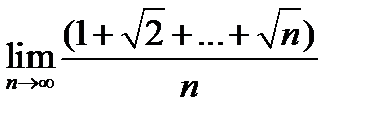6. 
.
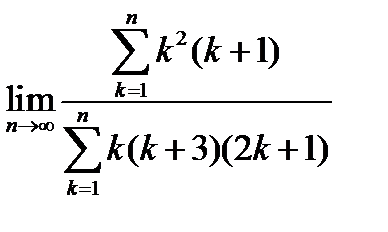7. 
.
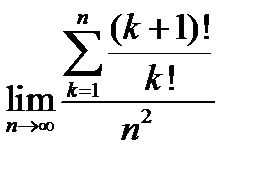8. 
.
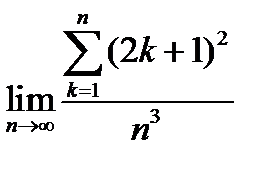9. 
.
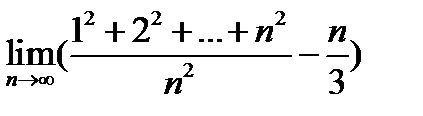10. 
.
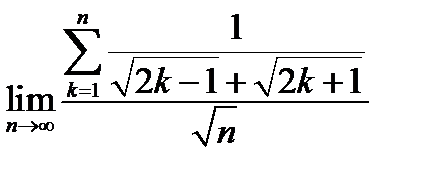11. 
.
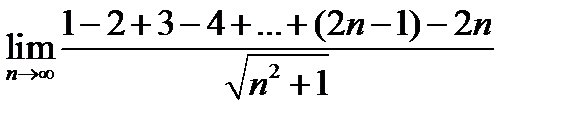12. 
.
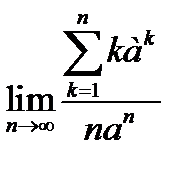13. 
.
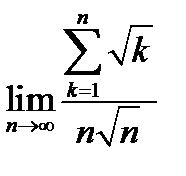14. 
.
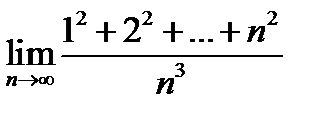15. 
.
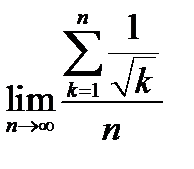16. 
.
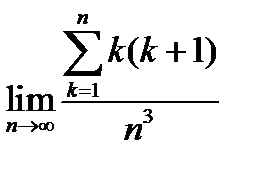17. 
.
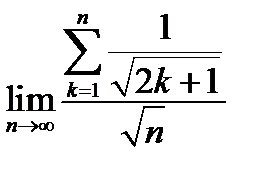18. 
;
19. 
;
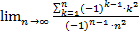20. 
;
21. 
;
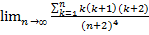22. 
;
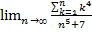23. 
;
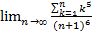24. 
;
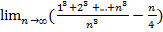25. 
;
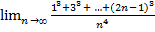26. 
;
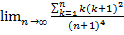27. 
;
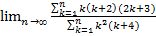28. 
;
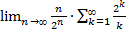29. 
;
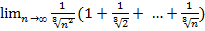30. 
.
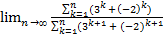Читайте також:
- Автомобільний пасажирський транспорт – важлива складова єдиної транспортної системи держави
- Володіння культурою мовлення – важлива умова професійного успіху та фахового зростання.
- ЛЕКЦІЯ 2. ЦІЛЕПОКЛАДАННЯ ЯК ВАЖЛИВА УМОВА ПРОЕКТУВАННЯ СУЧАСНИХ ОСОБИСТІСНО-ОРІЄНТОВАНИХ ПЕДАГОГІЧНИХ ТЕХНОЛОГІЙ.
- Лекція 4. Концепція ”навчання впродовж життя” як важлива складова Болонського процесу.
- Належність до певної статі – важлива особливість фенотипу особини.
- Тема 2.8. Форми та методи вирішення трудових спорів та конфліктів як важлива складова соціального партнерства.
- Утворення єдиної Помісної православної церкви в Україні– надзвичайно важлива проблема у духовному житті нашої держави.
- Фінансова політика як важлива складова економічної політики держави.
- Цілепокладання як важлива умова проектування сучасних особистісно-орієнтованих педагогічних технологій.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Методичні вказівки з проектування |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |