Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Плоска деформація і плоский напружений стан

Рішення плоскої задачі є одним з найважливіших питань прикладної теорії пружності. Пояснюється це тим, що дуже багато конструкцій або їх елементів працюють в умовах плоского напруженого стану або плоскої деформації, що й розглядається в плоскої задачі теорії пружності.

Плоский напружений стан виникає в тонкій пластинці, яка по торцевих сторонах навантажена силами, паралельними її основі, і рівномірно розподіленими по товщині (рис.3.1).

Рис.3.1. Пластинка в умовах плоского напруженого стану

У цьому випадку напруги 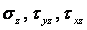на основах пластинки дорівнюють нулю. Так як пластинка тонка, то ці напруження дорівнюють нулю і по всьому обсягу пластинки, а інші компоненти тензора напружень ( 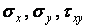) не залежать від z і є функціями тільки двох змінних — х и у.

Плоска деформація має місце, якщо переміщення відбуваються тільки паралельно площини ХОУ:

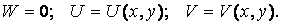
(3.1)

Такі переміщення відбуваються в довгому циліндричному або призматичному тілі при дії навантаження, яке перпендикулярно поздовжньої осі і постійної уздовж її. Цій розрахунковій схемі відповідають задачі про циліндричні котки, тунелі, підпірні стінки, греблях і т.п. (рис.3.2).

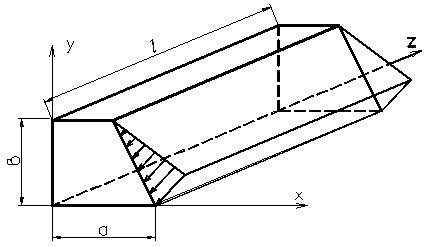
Рис.3.2. Плоска деформація

Якщо поздовжньою віссю є вісь Z, то в перерахованих випадках деформація виникає тільки в площині ХОУ:

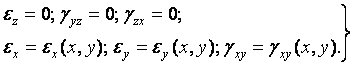
(3.2)

Незважаючи на відсутність деформації 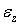, нормальні напруги 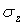будуть ненульовими, що треба з формули узагальненого закону Гука

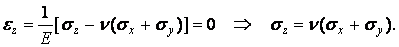
(3.3)

Плоский напружений стан і плоска деформація описуються практично однаковими рівняннями, відмінність складається тільки в значеннях пружних постійних. Ця обставина дозволяє об'єднати обидві задачі в одну - плоска задача теорії пружності.

Запишемо основні рівняння теорії пружності стосовно до випадку плоскої деформації.

Диференціальні рівняння рівноваги:

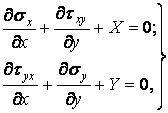
(3.4)

де X, Y — постійні по довжині об'ємні сили.

Умови на поверхні:

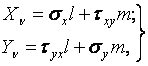
(3.5)

де l, m — напрямні косинуси.

Геометричні співвідношення Коші:

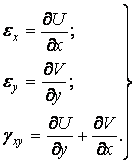
(3.6)

Рівняння нерозривності деформацій:

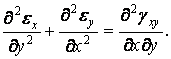
(3.7)

Формули закону Гука:

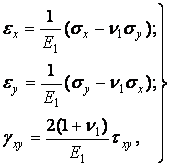
(3.8)

де

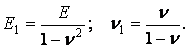
(3.9)

Для плоского напруженого стану рівняння (3.4) – (3.7) зберігають той же вид, а в рівняннях (3.8) 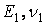переходять в.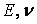

Таким чином, у плоскої задачі теорії пружності невідомими будуть вісім функцій (напружень , деформації 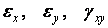, переміщення U, V), що відповідає числу рівнянь (два рівняння рівноваги, три геометричних співвідношення Коші й три формули закону Гука).

Залежно від того, які величини відомі, а які підлягають визначенню, розрізняють пряму задачу, зворотну і змішану. Основне значення для розрахунку конструкцій має пряме задачі; вона ж є й найбільш складною. Зворотне завдання вирішується значно простіше й має допоміжне значення.

Розрізняють наступні методи рішення прямої задачі: рішення в напруженнях, рішення в переміщеннях, змішаний метод.

Найбільше часто в практичних розрахунках необхідно визначати напруження . У цих випадках виконується рішення плоскої задачі в напруженнях.

Для реалізації такого підходу вводиться так звана функція напружень Эрі — , що пов'язана з напруженнями співвідношеннями

(3.10)

У результаті виходить рівняння

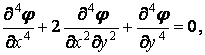
(3.11)

Яке називається бігармонічним рівнянням плоскої задачі теорії пружності.

Приєднання до нього умов на контурі, також виражених через функцію напруг Эрі,

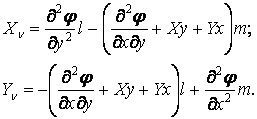
(3.12)

дозволяє визначити функцію напружень , а потім по формулах (3.10) — напруження.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	Методи рішення плоскої задачі для прямокутних однозв'язних областей

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.