
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Абсолютна деформація ділянки бруса тільки від власної ваги визначається за формулою
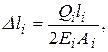 (1.3)
(1.3)
де  - вага
- вага 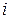 -ої ділянки (
-ої ділянки (  ;
; 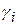 - питома вага матеріалу).
- питома вага матеріалу).
У випадку вертикального ступінчастого бруса, що защемлений знизу, деформація його 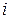 -ї ділянки сталого перерізу з урахуванням власної ваги знаходиться за формулою
-ї ділянки сталого перерізу з урахуванням власної ваги знаходиться за формулою

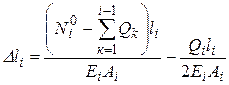 , (1.4)
, (1.4)
де  - зусилля в перерізах
- зусилля в перерізах 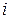 -ї ділянки без урахування власної ваги;
-ї ділянки без урахування власної ваги; 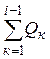 - сумарна вага усіх попередніх
- сумарна вага усіх попередніх  -тих ділянок (якщо йти від вільного кінця бруса).
-тих ділянок (якщо йти від вільного кінця бруса).
Абсолютна деформація бруса, що має декілька ділянок, дорівнює алгебраїчній сумі деформацій усіх його ділянок.
Переміщення якого-небудь перерізу знаходиться як алгебраїчна сума деформацій частин бруса, що розташовані між розглядуваним перерізом і закріпленим кінцем.
Відносна поздовжня деформація одноступінчастого бруса 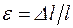 , де
, де  - довжина бруса. Деформація
- довжина бруса. Деформація  зв’язана з нормальним напруженням
зв’язана з нормальним напруженням 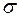 лінійною залежністю - законом Гука:
лінійною залежністю - законом Гука:  .
.
Відносна поперечна деформація 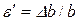 , де
, де  - ширина бруса. Деформація
- ширина бруса. Деформація  зв’язана з деформацією
зв’язана з деформацією 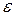 коефіцієнтом Пуассона (
коефіцієнтом Пуассона (  ) таким чином
) таким чином

 . (1.5)
. (1.5)
Для ізотропних матеріалів 0 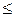

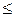 0,5.
0,5.
Умова міцності при осьовому розтяганні або стисканні має бути записана для небезпечного перерізу бруса, в якому виникає максимальне за модулем напруження

 , (1.6)
, (1.6)
де 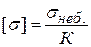 - допустиме нормальне напруження;
- допустиме нормальне напруження;  - небезпечне напруження, яке визначається експериментально при випробуванні стандартних зразків на розтягання та стискання;
- небезпечне напруження, яке визначається експериментально при випробуванні стандартних зразків на розтягання та стискання; 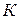 - коефіцієнт запасу міцності.
- коефіцієнт запасу міцності.
Для пластичних матеріалів  - границя текучості, а 1,4£
- границя текучості, а 1,4£ 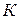 £2,5; для крихких матеріалів
£2,5; для крихких матеріалів 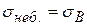 - границя міцності, а 2,5£
- границя міцності, а 2,5£ 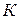 £5,0.
£5,0.
З умови міцності, якщо порівняти 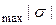 з
з 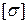 , можна визначити потрібну площу поперечного перерізу
, можна визначити потрібну площу поперечного перерізу
 , (1.7)
, (1.7)
або допустиму величину навантаження (  ); якщо
); якщо  , то
, то
 . (1.8)
. (1.8)
Для призматичного бруса постійного поперечного перерізу умова міцності з урахуванням власної ваги, якщо зосереджена сила та власна вага діють в одному напрямку, запишеться так
 ; (1.9)
; (1.9)
звідки можна знайти потрібну площу поперечного перерізу
 . (1.10)
. (1.10)
З виразу (1.9) видно, що напруження тільки від власної ваги бруса не залежить від площі поперечного перерізу.
Для ступінчастого бруса за допомогою (1.10) отримаємо вираз для визначення потрібної площі перерізу 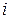 -ї ступені
-ї ступені
 . (1.11)
. (1.11)
Якщо зосереджена сила та власна вага діють в різних напрямках, то вирази (1.9-1.11) повинні відповідним чином корегуватися.
Власну вагу слід враховувати при розрахунках елементів, для яких вага є одним з основних навантажень (великі фундаменти, високі стіни, димові труби, довгі троси та т. ін.), а також у випадках використання матеріалів з малою питомою міцністю (  ).
).
Розпочинаючи розрахунок любої конструкції завжди спочатку треба встановити ступінь статичної невизначеності (ССН) розглядуваної системи. Для цього треба від кількості невідомих зусиль і незалежних від них реакцій конструкції відняти кількість можливих незалежних рівнянь статики, які можна скласти для наявної системи сил.
Для статично визначеної системи ССН=0, а для статично невизначеної ССН>0. Якщо система статично невизначена, то для її однозначного розрахунку рівнянь статики недостатньо, тому на основі розглядання деформації системи складають додаткові рівняння: рівняння сумісності або нерозривності деформацій. Необхідна кількість додаткових рівнянь дорівнює ССН.
Далі розглянуто приклади розрахунку двох задач на осьовий розтяг або стиск.
Приклад розв’язання задачі № 1.Ступінчастий бетонний брус (див. рис. 1.1,а та 1.3,а) перебуває під дією зосереджених зовнішніх сил і власної ваги. При  4 м,
4 м, 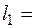 4 м,
4 м,  2 м,
2 м,  5 м,
5 м, 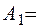 0,25 м2,
0,25 м2,  0,5 м2,
0,5 м2, 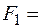 150 кН,
150 кН,  250 кН,
250 кН, 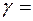 18 кН/м3,
18 кН/м3,  МПа та
МПа та 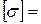 1 МПа, враховуючи та не враховуючи власну вагу, потрібно зробити наступне: а) побудувати епюри
1 МПа, враховуючи та не враховуючи власну вагу, потрібно зробити наступне: а) побудувати епюри 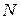 і
і 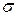 ; б) перевірити міцність бруса; в) визначити повну деформацію бруса; г) визначити переміщення перерізу І-І відносно жорсткого закріплення; д) користуючись умовою міцності знайти найбільш економічні за витратами матеріалу потрібні розміри квадратного поперечного перерізу кожної ділянки бруса.
; б) перевірити міцність бруса; в) визначити повну деформацію бруса; г) визначити переміщення перерізу І-І відносно жорсткого закріплення; д) користуючись умовою міцності знайти найбільш економічні за витратами матеріалу потрібні розміри квадратного поперечного перерізу кожної ділянки бруса.
Читайте також:
- Q6 розраховують тільки при нестаціонарному режимі
- ReM – модифікований критерій Рейнольда, який визначається за формулою
- А середній коефіцієнт росту в такому випадку визначається як
- А. Створення власної папки.
- Абсолютна величина дійсного числа
- Абсолютна величина можливих значень
- Абсолютна величина числа позначається символом .
- Абсолютна ентропія
- Абсолютна земельна рента.
- Абсолютна земельна рента.
- Абсолютна ідея (за Гегелем)
| <== попередня сторінка | | | наступна сторінка ==> |
| ОСЬОВИЙ РОЗТЯГ І СТИСК | | | Розв’язання задачі без урахування власної ваги |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |