• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ОСЬОВИЙ РОЗТЯГ І СТИСК

Осьовий розтяг або стиск – це деформація, яка виникає у тому випадку, коли зовнішні сили або їх рівнодійні направлені вздовж осі бруса.

Ось (вісь) бруса – це лінія, яка з’єднує центри ваги усіх поперечних перерізів.

Переріз найменшої площі називають поперечним (він завжди перпендикулярний до осі бруса).

Брус з прямолінійною віссю називають стержнем.

Дослідження показали, що при осьовому розтяганні або стисканні складові внутрішніх сил завжди перпендикулярні (нормальні) до поперечного перерізу. Рівнодійну вказаних складових називають поздовжньою або осьовою силою (зусиллям) та позначають літерою . Поздовжні розтягуючі сили вважають додатними, а стискуючі – від'ємними.

Для визначення поздовжніх сил використовують метод перерізів: розрізають брус (стержень) на дві частини; одну частину відкидають; вплив відкинутої частини на залишену заміняють поздовжньою силою, зображуючи її додатною, тобто направляючи від розглядуваного перерізу в бік відкинутої частини; складають можливі незалежні рівняння статики (рівняння рівноваги), з яких і визначають поздовжню силу.

Інтенсивність внутрішніх сил в точці називають напруженням (механічним напруженням). Розрізняють нормальні ( 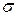) та дотичні ( 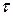) напруження. Нормальні напруження перпендикулярні до перерізу, а дотичні торкаються його.

Доцільно виділяти ділянки бруса (стержня). Межами ділянок є кінцеві перерізи бруса, а також перерізи, в яких прикладені зовнішні активні чи реактивні зосереджені сили, або відбувається різка зміна форми та розмірів поперечних перерізів.

При осьовому розтяганні або стисканні нормальні напруження по поперечному перерізу бруса (стержня), трохи віддаленому від місць прикладення зовнішніх активних та реактивних сил, розподілені рівномірно й на 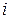-тій ділянці бруса визначаються за наступною формулою:

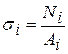, (1.1)

де 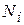- поздовжня сила, а - площа розглядуваного поперечного перерізу бруса (стержня).

Графічне зображення закону змінювання поздовжньої сили або нормального напруження за довжиною стержня відповідно називають епюрою повздовжніх сил ( ) або епюрою нормальних напружень ( ).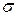

Якщо на і-тій ділянці бруса довжиною відношення 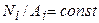, то абсолютна деформація цієї ділянки визначається за формулою

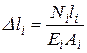, (1.2)

де 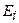- модуль пружності (модуль Юнга або модуль пружності першого роду) матеріалу бруса, який характеризує спроможність матеріалу опиратися деформуванню; - жорсткість при осьовому розтяганні або стисканні.

Читайте також:

1. А АА1В1В – осьовий переріз
2. Будьте обережними, коли виходите на вулицю. Пам'ятайте, що у ожеледицю найчастіше трапляються струси, переломи, вивихи, розтяги та розриви.
3. Випробування на розтяг (статичне випробування)
4. Вплив всесторонннього стиску і температури на механічні властивості гірських порід
5. Господарський роз-к Китаю в осьовий час та його ек.думка. 1 страница
6. Господарський роз-к Китаю в осьовий час та його ек.думка. 10 страница
7. Господарський роз-к Китаю в осьовий час та його ек.думка. 11 страница
8. Господарський роз-к Китаю в осьовий час та його ек.думка. 12 страница
9. Господарський роз-к Китаю в осьовий час та його ек.думка. 13 страница
10. Господарський роз-к Китаю в осьовий час та його ек.думка. 14 страница
11. Господарський роз-к Китаю в осьовий час та його ек.думка. 15 страница
12. Господарський роз-к Китаю в осьовий час та його ек.думка. 2 страница

Переглядів: 2053