• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

А АА1В1В – осьовий переріз

Особливу групу многогранників складають правильні многогранники. В означенні правильного многогранника нічого не говориться про їх існування. Саме тому доведемо наступну теорему, яку можна назвати теоремою про існування правильних многогранників.

Правильні многогранники та їх види.

Малюнок № 7.7. Трикутна піраміда.

С

О

А В SA, SB, SC – бічні ребра

SO – висота піраміди

Точка S – вершина піраміди.

Точка О – центр 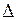ABC (точка перетину медіан)

Означення: піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти співпадає з центром цього многокутника.

Теорема: Різних видів правильних многогранників існує не більше п’яти.

Доведення:

Для доведення теореми будемо утворювати правильні многогранники, гранями яких будуть спочатку правильні трикутники, потім чотирикутники (квадрати), потім п’ятикутники і таке інше. Утворивши їх, ми будемо з’ясовувати існують вони чи ні. При доведенні теореми нам доведеться спиратися на деякі твердження, а саме: 1) в одній вершині многогранного кута може сходитися не менше трьох граней; 2) сума плоских кутів многогранного кута менша за 360º; 3) сума внутрішніх кутів многокутника обчислюється за формулою 2d(n-2), де d=90º, а n – це кількість сторін многокутника; 4) щоб знайти величину внутрішнього кута правильного многокутника, слід суму його внутрішніх кутів поділити на кількість сторін.

Оскільки найпростішим правильним многокутником є трикутник, то з’ясуємо чи існують правильні многогранники, гранями яких є правильні трикутники. Відомо, що кожен кут правильного трикутника дорівнює 60º. Нехай в одній вершині многогранника сходиться три трикутника. Тоді сума плоских кутів многогранного (тригранного) кута дорівнює 60º•3=180º<360˚, а тому такий правильний многогранник існує. Його називають тетраедром і він має 4 грані, 4 вершини і 6 ребер, що відповідає вимогам теореми Л.Ейлера, бо 4+4-6=2. Грані цього многогранника є правильні трикутники. Цей многогранник являє собою трикутну піраміду, всі грані якої правильні трикутники.

Нехай в одній вершині многогранника сходиться чотири трикутника. Тоді сума плоских кутів многогранного (чотиригранного) кута дорівнює 60º•4=240º< 360˚, а тому такий правильний многогранник існує. Його називають октаедром і він має 8 граней, 6 вершин і 12 ребер, що відповідає вимогам теореми Л.Ейлера, бо 8+6-12=2. Грані цього многогранника є правильні трикутники. Цей многогранник являє собою дві чотирикутні піраміди, які зіставлені основами, але всі грані якої правильні трикутники.

Нехай тепер в одній вершині многогранника сходиться п’ять трикутників. Тоді сума плоских кутів многогранного (п’ятигранного) кута дорівнює 60º•5=300º<360˚, а тому такий правильний многогранник існує. Його називають ікосаедром і він має 20 граней, 12 вершин і 30 ребер, що відповідає вимогам теореми Л.Ейлера, бо 20+12-30=2. Грані цього многогранника є правильні трикутники.

Нехай в одній вершині многогранника сходиться шість трикутників. Тоді сума плоских кутів такого многогранного кута дорівнює 60º•6=360º, тобто сума плоских кутів многогранного кута не менша за 360˚. Саме тому такого правильного многогранника, в одній вершині якого сходиться шість трикутників, існувати не може. Отже, правильних многогранників, гранями, якого є трикутники є три види: тетраедр, октаедр і ікосаедр.

Наступним видом правильних многокутників є правильний чотирикутник, тобто квадрат. Відомо, що кожен кут квадрата дорівнює 90º. З’ясуємо чи існують правильні многогранники, гранями яких є квадрати. Нехай в одній вершині многогранника сходиться три квадрати. Тоді сума плоских кутів многогранного (тригранного) кута дорівнює 90º•3=270º<360˚, а тому такий правильний многогранник існує. Його називають гексаедром або кубом і він має 6 граней, 8 вершин і 12 ребер, що відповідає вимогам теореми Л.Ейлера, бо 6+8-12=2. Грані цього многогранника є правильні чотирикутники (квадрати). Цей многогранник являє собою прямокутну призму, всі грані якої правильні чотирикутник. Нехай в одній вершині многогранника сходиться чотири квадрати. Тоді сума плоских кутів такого многогранного кута дорівнює 90º•4=360º, тобто сума плоских кутів многогранного кута не менша за 360˚. Саме тому такого правильного многогранника, в одній вершині якого сходиться чотири квадрати, існувати не може. Отже, існує лише один вид правильних многогранників, гранями, якого є квадрати. Це гексаедр або куб.

Перед тим, як з’ясувати, чи існують правильні многогранники, гранями яких є правильні п’ятикутники, визначимо величину внутрішнього кута правильного п’ятикутника. Суму внутрішніх кутів будь-якого п’ятикутника обчислюємо за формулою 2d(n-2), де d=90º і n=5. Отже, 2•90º•(5-2)=180º•3=540º. Тоді кожен кут правильного многогранника дорівнює 540º:5=108º. Нехай в одній вершині многогранного кута сходиться три правильних п’ятикутника. Сума плоских кутів такого многогранного кута дорівнює 108º•3=324º<360˚, тобто такий многогранник існує. Його називають додекаедром і він має 12 граней, 20 вершин і 30 ребер, що відповідає вимогам теореми Л.Ейлера, бо 12+20-30=2. Грані цього многогранника є правильні п’ятикутники. Оскільки 108˚•4=432º, що більше за 360˚, то правильних многогранників, в одній вершині якого б сходилося чотири правильних п’ятикутника, не існує. Таким чином, існує лише один вид правильних многогранників, гранями якого є правильні п’ятикутники, - це додекаедр.

Легко показати, що гранями правильного многогранника не можуть бути правильні шестикутники, семикутники, восьмикутники тощо. Отже, існує всього п’ять видів правильних многогранників. Це, по-перше, тетраедр, октаедр і ікосаедр, гранями, яких є правильні трикутники; по-друге, гексаедр або куб, гранями, якого є квадрати; по-третє, додекаедр, гранями якого є правильні п’ятикутники. Таким чином, існує всього п’ять видів правильних многогранників. Теорему доведено.

3. Поняття тіла обертання, їх види (циліндр, конус, куля. сфера) та їх зображення на площині.

3. Наступним видом геометричних фігур є тіла обертання. Наведемо означення цих фігур та їх елементів.

Означення: циліндром називається тіло, яке складається із двох кругів, що сполучаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. малюнок № 7.8.).

А₁

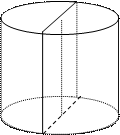О₁ ОО₁ – вісь циліндра

В₁ ОА=ОВ=О₁А₁=О₁В₁ – радіуси основ

АА₁=ВВ₁ – твірні циліндра

Читайте також:

1. Вибір перерізу провідників у мережах напругою до 1000 В з урахуванням плавких запобіжників
2. Вибір перерізу провідників у мережах напругою до 1000В з урахуванням автоматичних вимикачів і теплових реле
3. Визначення потрібної площі перерізу стояка.
4. Внутрішні сили. Метод перерізів
5. Геометричні характеристики деяких перерізів
6. Геометричні характеристики поперечного перерізу
7. Головні осі інерції та головні моменти інерції перерізу
8. Головні осі інерції та головні моменти інерції перерізу
9. Господарський роз-к Китаю в осьовий час та його ек.думка. 1 страница
10. Господарський роз-к Китаю в осьовий час та його ек.думка. 10 страница
11. Господарський роз-к Китаю в осьовий час та його ек.думка. 11 страница

Переглядів: 1099