Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Тема 3. Арифметичні операції в двійковій СЧ. Додавання і віднімання чисел.

Основною операцією, яку використовують у цифрових системах під час виконання різних обчислень, є операція алгебраїчного додавання. її виконують на основі правил виконання операцій у двійковій системі зображення чисел, які для однорозрядних чисел мають такий вигляд:

Перенесення до старшого розряду здійснюють тоді, коли в одному розряді обох складових є одиниці. Операцію знаходження суми у багаторозрядних числах виконують послідовно, починаючи з молодшого розряду. У зв'язку з цим, починаючи з другого розряду, виконують складання трьох цифр - двох розрядних складових і перенесення з молодшого розряду.

Приклад 3.1. Скласти два додатні двійкові числа .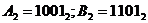

Розв'язання. Під час виконання операції додавання мають місце переповнення у першому та четвертому розрядах і, відповідно, перенесення одиниці з першого розряду у другий і з четвертого у п'ятий.

Операцію віднімання у цифрових схемах виконують за допомогою операції додавання, зображуючи від'ємник у доповняльному коді.

Приклад 3.2. Знайти суму двох чисел і з використанням доповняльного коду.

Розв'язання. Для виконання вказаної операції у десятковій системі числення необхідно для числа K знайти відповідний доповняльний код. Його знаходять за тими ж правилами, що й у двійковій системі. Обернений код числа знаходять як доповнення до дев'ятки цифри кожного розряду. Для числа 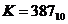обернений код

Доповняльний код для числа К:

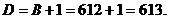
Виконаємо операцію додавання. При цьому введемо знакові розряди, які позначимо апострофом, що встановлюєтьсяпісля знакової цифри:

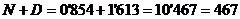
Перенесення, що з'являється зі знакового розряду, відкидаємо.

Аналогічно виконують операцію віднімання у двійковій системі числення.

Приклад 3.3. Додати два числа 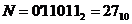і

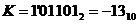
Розв'язання. Знаходимо доповняльний код від'ємного числа K:

Знаходимо суму:

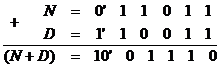
Відкидаючи 1 переносу у знаковому розряді, отримуємо:

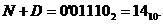
Приклад 3.4. Змінимо знаки обох чисел на зворотні:

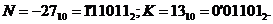
Розв'язання. Доповняльний код від'ємного числа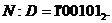

Знаходимо суму:

Знаковий розряд засвідчує, що результат операції від'ємний, а число зображене у доповняльному коді. Для отримання результату у прямому коді необхідно спочатку перейти до оберненого коду, віднімаючи одиницю від результату виконання арифметичної операції, а потім - інвертувати.

Знаходимо обернений код результату: прямий код:

Пряму операцію віднімання з використанням операцій позичення зі старших розрядів застосовують лише для порівняння двох кодів, адже відсутність чи наявність позичення зі старшого розряду дає можливість легко визначити більше з порівнюваних чисел.

Розглянемо тепер особливість виконання операцій у двійково-десятковій системі числення (код 8-4-2-1). Виконують операції на основі правил двійкової арифметики. Якщо одержане число перевищує 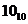, то повинна формуватися одиниця перенесення, яка передається до наступного десяткового розряду. Але результат відрізнятиметься від правильного, і в нього необхідно внести відповідний коректив. Наявність у результаті операції числа, що перевершує дев'ятку, легко виявляють за рядом ознак, які читач може сформулювати самостійно.

Приклад 3.5. Скласти числа і використанням коду 8-4-2-1.

Розв'язання. Оскільки результат менший десяти, то корекція не потрібна.

Приклад 3.6. Скласти числа 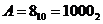і

Розв'язання. 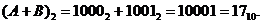У цьому випадку результат більший десяти, тому необхідно вносити корекцію.

Поява одиниці у п'ятому розряді означає, що число, представлене чотирма молодшими розрядами, збільшилось на 16 одиниць. Але, з іншого боку, одиниця передалась у старший десятковий розряд, що еквівалентно числу 10, тому в молодшому розряді не вистачає шістьох одиниць. Це означає, що необхідно до результату додати корекцію - шість одиниць, тобто:

Результат представлено одиницею в розряді десятків і сімкою в розряді одиниць.

Приклад 3.7. Скласти числа

Розв’язання :

У цьому прикладі перенесення у п'ятий розряд немає, але результат перевершує дев'ятку, тому необхідно внести корекцію. Корекція необхідна не тільки для того, щоб скоригувати результат молодших розрядів, а й для того, щоб перенести одиницю у старший десятковий розряд. Знову додасться 10 і відніметься 16, тому для корекції необхідно додати цифру 6:

З двох останніх прикладів бачимо, що у першому випадку під час виконання операції має місце перенесення у старшу тетраду, що і може виступати ознакою необхідності корекції результату. У другому випадку такого перенесення немає, тому необхідно або передбачати можливість такого результату, або створювати допоміжні заходи для введення корекції. Як вихід з такої ситуації можна запропонувати використання самокоригувальних кодів -наприклад коду "з надлишком З".

Приклад 3.8. Виконати операцію знаходження суми двох чисел з попереднього прикладу у випадку використання коду "з надлишком З".

Розв'язання. Відповідні коди чисел: 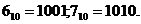Після виконання операції додавання маємо результат:

У разі використання інших кодів для зображення десяткових Цифр правила знаходження суми зміняться, але логічний аналіз процедури легко дозволяє знайти правила корекції.

У випадку знаходження суми багаторозрядних двійково-десяткових чисел від'ємні числа зображують в оберненому або доповняльному коді. При цьому обернений код одержують за рахунок доповнення до 9. Якщо використовувати не код 8-4-2-1, а коди "з надлишком 3" або 2-4-2-1, то процедура формування доповнення до 9 значно спрощується.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Тема 2. Подання інформації в електронно-обчислювальних машинах.	\|	Тема 4. Двійкова СЧ. Виконання операцій множення

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.